【学习打卡】【ELT.ZIP】OpenHarmony啃论文俱乐部——快速随机访问字符串压缩

++综述视角解读压缩编码++

本文出自ELT.ZIP团队，ELT<=>Elite(精英)，.ZIP为压缩格式，ELT.ZIP即压缩精英。
成员：
- 上海工程技术大学大二在校生
- 合肥师范学院大二在校生
- 清华大学大二在校生
- 成都信息工程大学大一在校生
- 黑龙江大学大一在校生
- 华南理工大学大一在校生
我们是来自6个地方的同学，我们在OpenHarmony成长计划啃论文俱乐部里，与华为、软通动力、润和软件、拓维信息、深开鸿等公司一起，学习和研究操作系统技术…

@[toc]

【往期回顾】

【本期看点】

FSST思想内核
FSST的演化
FSST与LZ4对比
亲手复现FSST

【技术DNA】

【智慧场景】

**********	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	********************	*****************
场景	自动驾驶 / AR	语音信号	流视频	GPU 渲染	科学、云计算	内存缩减	科学应用	医学图像	数据库服务器	人工智能图像	文本传输	GAN媒体压缩	图像压缩	文件同步	数据库系统
技术	点云压缩	‎稀疏快速傅里叶变换‎	有损视频压缩	网格压缩	动态选择压缩算法框架	无损压缩	分层数据压缩	医学图像压缩	无损通用压缩	人工智能图像压缩	短字符串压缩	GAN 压缩的在线多粒度蒸馏	图像压缩	文件传输压缩	快速随机访问字符串压缩
开源项目	Draco / 基于深度学习算法/PCL/OctNet	SFFT	AV1 / H.266编码 / H.266解码/VP9	MeshOpt / Draco	Ares	LZ4	HCompress	DICOM	Brotli	RAISR	AIMCS	OMGD	OpenJPEG	rsync	FSST

FSST

快速静态符号表(FSST)压缩，这是一种轻量级的字符串编码方案。

引言：

::: hljs-left

• 字符串在现实世界的数据集中很普遍。它们通常占用大量数据，处理速度很慢。
• 在许多真实的数据库中，很大一部分数据是用字符串表示的。
• 这是因为字符串经常被用作各种数据的万能类型。
• 人工生成的文本(描述或评论字段)

:::

• 机器生成的标识符(url、电子邮件地址、IP 地址）

1. 字符串处理的现有方案

• 字符串通常是高度可压缩的，许多系统依赖字典来压缩字符串。但是字典压缩需要完全重复字符串来减少大小，因此当字符串相似但不相等时，字典压缩没有优势。存储在数据库中的大多数字符串每个字符串通常小于 30 字节。LZ4 就不适合压缩小的、单个的字符串，因为它们需要达到 KB 数量级的输入大小才能获得良好的压缩因子。但是，数据库系统通常所需是对单个字符串随机访问，而LZ4算法是通过对数据块的访问实现的，这就无法满足数据库系统的需求。

2.主要特点

• 随机访问(解压缩单个字符串而无需解压缩一个更大的块的能力)
• 快速解码(≈1-3 周期/字节，或 1-3 GB/s 每个核)
• 文本字符串数据集的良好压缩因子(≈2×)
• 高编码性能(≈4 个周期每字节，或≈1 GB每秒每字节)

3.关键思想

• 是用 1 字节代码替换频繁出现的最多 8 字节的子字符串，这些元素构成一个不可变符号表。

4.前人的积淀

• 数据库系统轻量级压缩的研究集中在整数数据，但字符串在现实工作负载中的普遍存在和性能挑战需要进行更多的研究。压缩字符串最常用的方法是使用
字典重复数据删除。字典将每个唯一的字符串映射为整数代码，使用整数压缩方案对这些代码进行压缩。在大多数数据库系统中，字符串本身没有被压缩。

Binnig 等人提出了一个带增量前缀压缩的保序字符串字典。
字典被表示为一个混合的 try /B-tree 数据结构，以排序的顺序存储唯一的字符串。虽然对某些数据集(例如 url)有效，但许多其他常见字符串数据集(例如 uuid)没有长时间的共享前缀，这使得该方案无效。全局字典还有如更新昂贵等缺点，这阻碍了它们的广泛采用。
另一种压缩字符串字典的方法是由 Arz 和 Fischer提出
他们开发了 LZ78的变体，允许解压单个字符串。但是，这种方法的解压缩非常昂贵，对于平均长度为 19 的字符串，需要超过 1 微秒的时间。这相当于每个字符大约 100 个 CPU 周期或每秒几十兆字节，这对于许多数据管理用例来说太慢了。
PostgreSQL
不使用字符串字典，而是实现了一种叫做 “超大属性存储技术”(TOAST)的方法。大于 2 KB 的进行压缩，较小的值保持不压缩。
字节对
此方案是少数允许解压缩单个短字符串的压缩方案之一。它首先对数据执行一次完整的传递，确定哪些字节值没有出现在输入中，并计算每对字节出现的频率。然后用未使用的字节值替换最常见的字节对。重复这个过程，直到没有更多未使用的字节。字节对对未使用字节的依赖意味，给定一个现有的压缩表，不可见的数据不能被压缩。字节对的递归性质使解压缩迭代，速度很慢。
递归配对
一种随机访问压缩格式，它递归地构造层次符号语法。初始语法由所有单字节符号组成，通过将源文本中频率最高的连续符号对替换为一个新符号、相对于扩展的语法重新计算所有符号对的频率，并递归地进行扩展。
主要步骤
制静态符号表
识别经常出现的公共子字符串(称之为符号)，并将它们替换为短的、固定大小的代码，由于效率的原因，符号的长度在 1 到 8 字节之间，并在字节(而不是位)边界上进行标识。代码总是 1 字节长，这意味着最多可以有 256 个符号，其中一个码被保留为转义码.
解压缩
解压缩是相当简单的。每段代码都通过数组查找转换为其符号，并将符号追加到输出缓冲区。为了有效地解压缩，将每个符号表示为一个 8 字节(64 位)的单词，并将所有符号存储在一个数组中。此外，还有第二个数组，用于存储每个单词的长度。使用这种表示，可以无条件地将 64 位字存储到输出缓冲区中，然后将输出缓冲区向前推进符号的实际长度来解压代码，依赖于现代处理器上可用的快速未对齐存储，这种实现需要很少的指令，而且没有分支。它的缓存效率也很高，因为符号表(2048 字节)和长度数组(256 字节)都可以轻松地放入一级 CPU 缓存中。
几点解释
::: hljs-left

1.使用转义字符的优势
PS：（转义码并不是严格必要的;也可以只使用那些没有出现在输入字符串中的字节作为代码）
直接原因：保留代码 255 作为转义标记，表示输入中的以下字节需要按原样复制，而不需要在符号表中查找。
三个优点
（1）支持使用现有的符号表压缩任意(看不见的)文本。
（2）允许在数据样本上执行符号表构造，从而加速压缩。
（3）它释放了原本被保留为低频字节的符号，从而提高了压缩因子。

2.连续注入单字节符号
如果由两个较短的符号合并创建一个较长的符号，如果较长的符号再之后的增益排序中处于末尾就会被其他增益较长的字符串取代，这也就意味着原先那两个较短的字符串也就随之消失。
从本质上说，如果不考虑单字节，符号只会变长，如果这样更好的话，就永远不可能回到更短的符号。连续注入单字节符号允许重新生长由于这种太贪婪的选择而丢失的有价值的长符号。

FSST良好属性

保有字符串属性：不会因为编码转化变成其他类型的文本。
压缩查询处理。直接通过比较其再表中的符号即可。
字符串匹配。也可以对压缩的字符串执行更复杂的经常发生的字符串操作(例如，LIKE 模式匹配)，通过转换为字节流中识别它们而设计的自动机，将它们重新映射到代码流中。
符号表很小。符号表的最大大小为 8*255+255 字节，但通常只占用几百字节，因为平均符号长度通常在 2 左右。因此，使用单独的符号表压缩每个字符串列的每个页面是完全可行的，但也可以采用更粗粒度的粒度(按行组或整个表)。更细粒度的符号表构造会带来更好的压缩因子，因此符号表将更适合于压缩的数据。
并行性。由于没有(解)压缩状态，FSST(解)压缩并行化很简单——只有符号表构造算法可能需要序列化。另一方面，让每个批量加载数据块的线程构造一个单独的符号表 (应该放在每个块头中)也是可以接受的，这样压缩也会变得非常并行。
0-terminated 字符串。FSST 可选地生成以 0 结尾的字符串，因为在以 0 结尾的字符串中字节只出现在每个字符串的末尾，实际上还有 254 个代码需要压缩。这稍微降低了压缩的级别(价值最低的 255 个符号必须从符号表中删除，它的出现将使用转义字节进行处理)，但这种可选模式允许 FSST 适应许多现有的基础结构。

:::

5.存在问题

重复
首先计算长度为 1 到 8 的子字符串在数据中出现的频率，然后根据增益顺序选择前 255 个符号。这种方法的问题是:选择的符号可能重叠，因此计算的增益会被高估。例如，在 URL 数据集中，8 字节符号 http://w 几乎每个字符串都含有，最有希望被选中。但符号 ttp://ww 和 tp://www 看起来同样有希望，将所有三个候选者添加到符号表中是对有限代码数量的浪费，并会对压缩因子产生负面影响。
贪婪性
在编码期间贪婪地选择最长的符号不一定能最大化压缩效率。参考我们在上文提到的连续单字节注入.
综上所述，符号重叠与贪婪编码相结合，造成符号之间的依赖问题，这使得难以估计增益，从而创建良好的符号表。

优化方案

::: hljs-left

（1)迭代语料库，使用当前的符号表动态编码。这个阶段计算符号表的整体质量(压缩因子)，但也计算每个符号在压缩表示中的出现频率，以及每个连续符号对。
(2)利用这些计数，通过选择表观增益最高的符号来构建一个新的符号表。
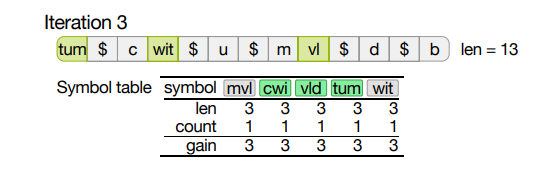
实例
语料库“tumcwitumvldb”上的 4 次迭代。为了使示例易于说明，将最大符号长度限制为 3(而不是 8)，最大符号表大小限制为 5(而不是 255)。在每次迭代之后，在顶部显示压缩后的字符串，但为了可读性，不显示代码，而是显示相应的符号。“$”表示转义字节。

:::

这是最初未压缩的字符串

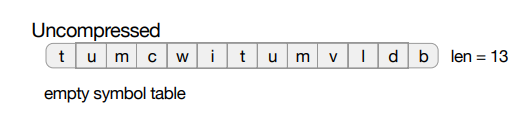
在第一次迭代中，压缩字符串的长度临时加倍，因为符号表最初是空的，每个符号都必须转义。在图的底部，我们显示了符号表，前 5 位符号基于静态增益。

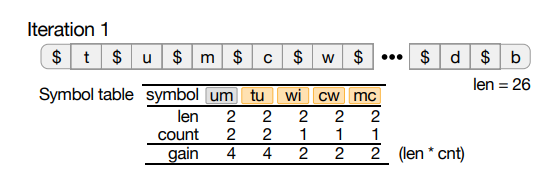
迭代 1 后，静态增益排名前 5 位的为“um”、“tu”、“wi”，“cw” 和 “mc”。前两个最上面的符号(“um”，“tu”)出现了两次，因此增益为 4，而后三个符号(“wi”，“cw”和“mc”)只出现一次，因此增益为 2。注意，符号“mv”，“vl”，“ld”，“db”， “m”，“t”，“u”的增益也为 2，也可以被选取。换句话说，当选择顶部符号时，算法会任意地选取。

在第 2、3 和 4 次迭代中，符号表的质量稳步提高。

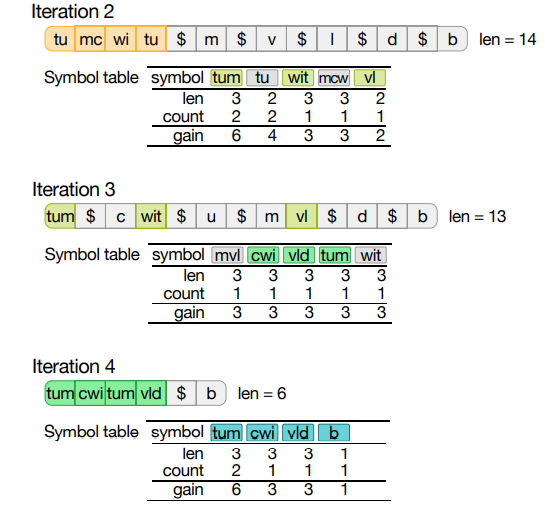
迭代 4 之后，最初长度为 13 的语料库被压缩为 5。
图中还显示，算法也会出现错误，但这些错误会在下一次迭代中得到修复。
例如，在第 2 次迭代中，符号“tu”看起来相当有吸引力，静态增益为 4，但由于“tum”也在符号表中，“tu”最终变得毫无价值

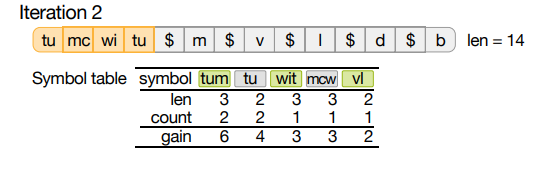
并在第 3 次迭代中被修正

技术优化：
AVX512压缩

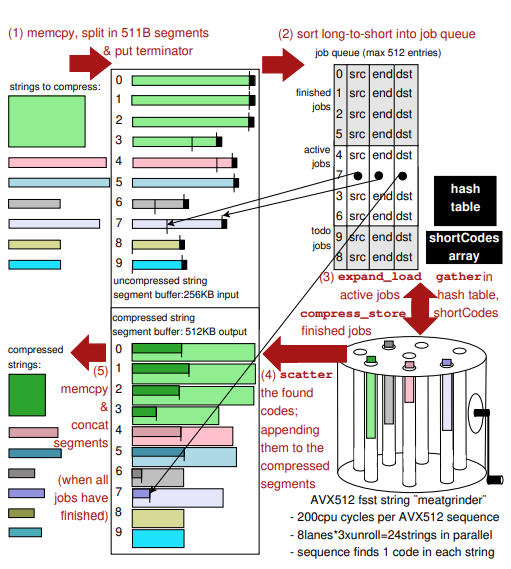
第一步，FSST API 压缩一批字符串，字符串被复制到一个由 512 个段组成的临时缓冲区中，如果需要将分割长字符串，并添加终止符。
第二步，首先按反向字符串长度对作业队列数组进行基数排序——速度很快，只需一次传递——因此首先处理最长的字符串，这有助于负载平衡。作业可能以不连续的顺序完成，因此由于排序而以不连续的作业顺序开始编码工作，不会使算法(进一步)复杂化。
第三步，AVX512 的优势不是内存访问，而是在压缩内核中利用的并行计算。不只是一次性启动 SIMD 内核来处理 8 个通道中的 8 个字符串(或 24 个通道中的 24 个字符串，3×展开)，因为有些字符串会比其他字符串短得多，而有些字符串会比其他字符串压缩得多。这将意味着在编码工作结束时，许多通道将是空的。因此，缓冲 512 个作业，并在需要时在每次迭代中重新填充车道。退出作业(作业控制寄存器中的通道 )使用compress_store 指令，并填充 expand_load 指令。

FSST 与LZ4对比

· 速度

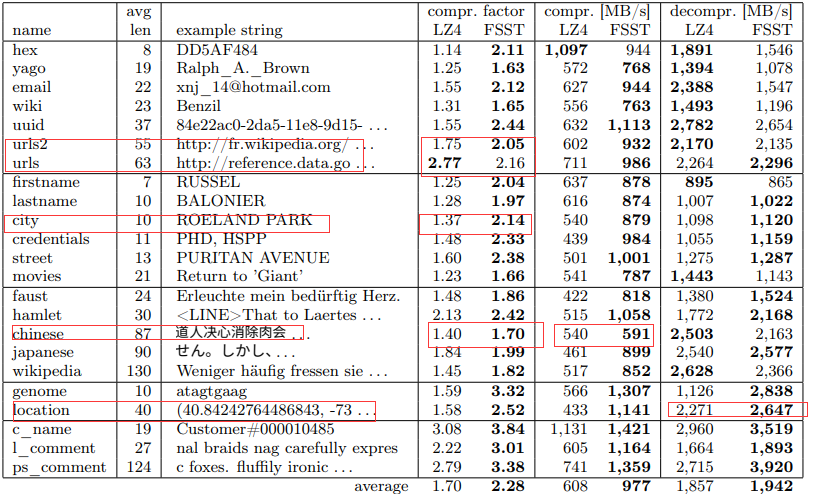
上表显示了 LZ4 和 FSST 在每个数据集上分别和平均的三个指标的相对性能。

对于几乎所有的数据集，FSST 在压缩因子和压缩速度方面都优于 LZ4。平均而言，除了产生更好的压缩因子 FSST 的压缩速度也提高了 60%。对于解压速度，FSST 在某些数据集上更快，而 LZ4 在其他数据集上更快——平均速度几乎相同。

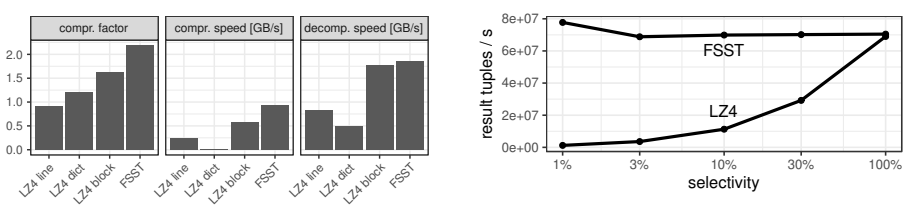
· 随机存取
在数据库场景中，通常不存储大文件，而是使用包含大量相对较短字符串的字符串属性或字典。用 LZ4 单独压缩这些字符串会得到非常差的压缩系数，普通 LZ4 (LZ4 行)不能合理地处理短字符串—压缩因子低于 1，这意味着数据大小实际上略有增加。LZ4 还可选地支持使用额外的字典，该字典需要与压缩数据一起提供。使用 zstd 预生成一个适合语料库的字典(LZ4 字典)，在一定程度上提高了压缩因子，但严重影响了压缩速度。
下图是测试结果

· 分文本数据
数据库环境之外，压缩社区经常评估 Silesia 语料库上的压缩方法，该语料库由 11 个文件组成，其中 4 个是文本文件(dick- ens, reymont, mr, webster)，1个是 XML, 6 个是二进制文件。FSST 对文本文件的压缩大小平均提高了 10%，但对二进制文件的压缩大小平均降低了 25%。虽然认为二进制文件与 FSST 无关，但它在大型 XML 和 JSON 文件上的压缩比比 LZ4 差 2-2.5 倍，这是相关的。但是，数据库系统不应该将这些组合值存储为简单的字符串，而应该存储为允许查询处理的特殊类型。例如，Snowflake 识别 JSON 列中的结构，并在内部将
每个经常出现的 JSON 属性存储在单独的内部列中。

FSST的演化

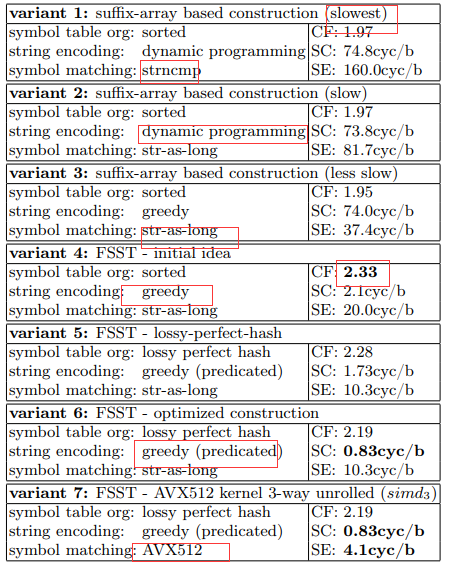
FSST 压缩算法经过多次迭代才达到当前的设计。上表显示了 7 种变体的压缩因子(CF)、符号表构建成本(CS)和字符串编码速度(SE)
第一个设计基于后缀数组，压缩因子达到1.97，但符号表的构造需要 74.3 cy- cles/字节，编码需要 160 cycles/字节。
目前的 AVX512 版本(图中的变体 7)在表构建方面快了 90 倍，快了40倍用于编码比第一个版本-同时提供更高的压缩因子。
最终的版本也比最初的 FSST 版本(变体 4)快得多，这要归功于损耗完美哈希和 AVX512——尽管不得不牺牲相对于变体 4 大约 6%的空间增益。
尽管需要多次迭代，但符号表的构造时间只占编码时间的一小部分。优化构造需要将迭代次数从 10 次减少到 5 次，构建一个示例(每次迭代都会增长)，并缩小计数器的内存占用。

复现流程

系统需求

Linux、Windows、MacOS 均可，此处为 Deepin 20.5 / Linux 环境

源码准备

首先，来到 FSST 的开源仓库 https://github.com/cwida/fsst，在已配置 Git 环境的情况下可以按照如图所指位置复制 https 或 ssh 地址将源码克隆至本地；若未配置 Git，可参考 github 或 gitee 的相关指示进行配置操作。不过，Git 在此处并非必要条件，也可手动 "Download ZIP" 得到压缩包后进行解压。
如上所述，针对 Git 环境，在终端中键入以下命令：
git clone https://github.com/cwida/fsst.git # 若已配置SSH公钥，可采用下图形式
cd fsst/

环境搭建

CMake 安装

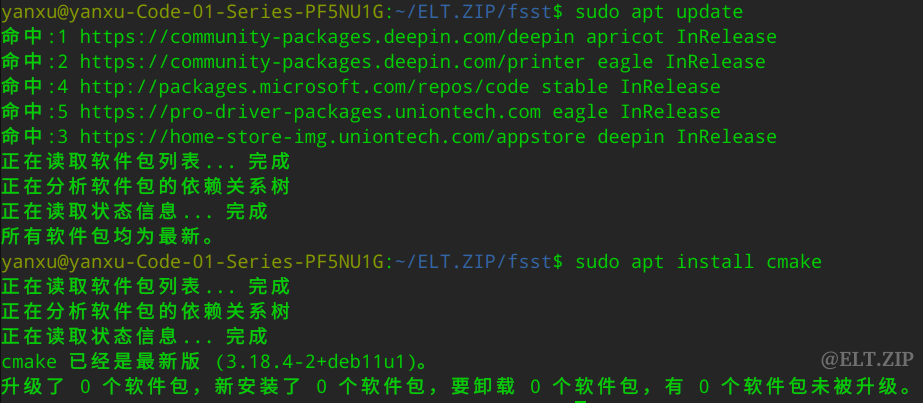
FSST 使用 C++ 语言实现，因此依赖 CMake 工具进行编译构建，Debian 系下可方便地使用 apt 实现工具安装初始化，键入并执行以下命令：

sudo apt update
sudo apt install cmake
sudo apt install cmake

可以看到 cmake 在之前已经安装过了，并且版本是 3.18.4 ：

Zstd 与 LZ4 库的安装

FSST 需要调用 zstd 与 lz4 的相关 API 以在压缩过程中生成对应字典，因此还需要准备相应的动态库：

sudo apt install zstd* lz4* libzstd* liblz4*   # 同 cmake 的安装
sudo apt install zstd* lz4* libzstd* liblz4*   # 同 cmake 的安装

完成后，可以在 /usr/lib/x86_64-linux-gnu/ 下看到相关文件已生成：

此外，还需要建立到 /usr/lib/ 的软链接，避免后续链接时出现找不到缺省目录的问题：

# 注意，下方诸如 '1.4.8' '1.8.3' 一类的版本号需要根据实际状况进行相应地替换
cd /usr***/lib/x86_64-linux-gnu/
echo '../libzstd.so ../libzstd.so.1 ../libzstd.so.1.4.8' | sudo xargs -n 1 ln -s libzstd.so.1.4.8
echo '../liblz4.so ../liblz4.so.1 ../liblz4.so.1.8.3' | sudo xargs -n 1 ln -s liblz4.so.1.8.3
echo '../liblz4.so ../liblz4.so.1 ../liblz4.so.1.8.3' | sudo xargs -n 1 ln -s liblz4.so.1.8.3

编译构建

环境部署基本完成，下面开始编译。

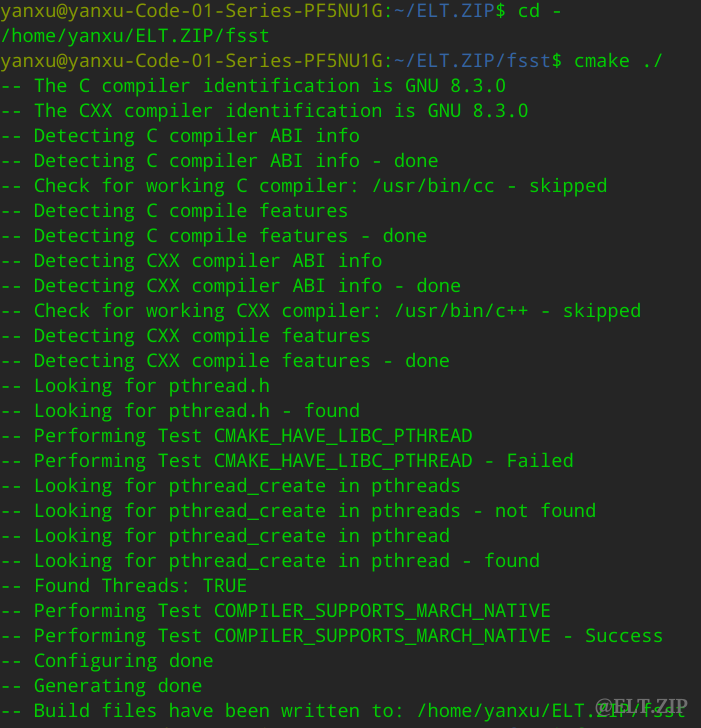
cd -
cmake ./
make -j8 && make binary
make -j8 && make binary

100% 完成后，说明编译已成功，查看所在目录，可以看到 fsst 的二进制程序已生成：

为了方便后续操作，建议将其加入环境变量：

vim ~/.bashrc
export PATH=/home/yanxu/ELT.ZIP/fsst:$PATH    # 在尾行添加
:wq    # 保存退出
:wq    # 保存退出

已经可以正常使用，输入 fsst 即可查看说明：

评估测试
自动化测试

仓库中提供了足量的数据集用来对算法进行评估，并且也有自动化脚本帮助一键跑完全程，下面就来试一试吧：

cd paper/
chmod +x *.sh
chmod +x *.sh

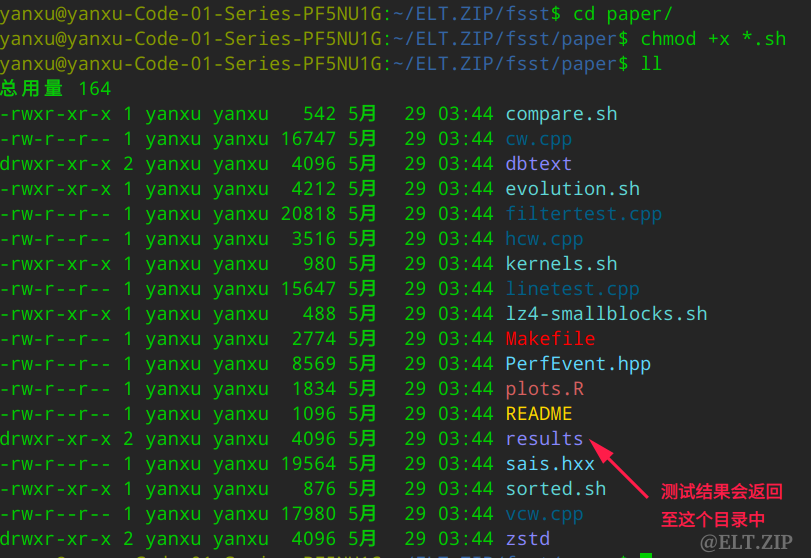
results 目录中已存放有作者测试过的结果，但我们同样可以在自己机器上再进行一遍测试，执行如下命令：

make experiments
make experiments

花费时间会较长，耐心等待即可，这里举出作者的其中一项示例：

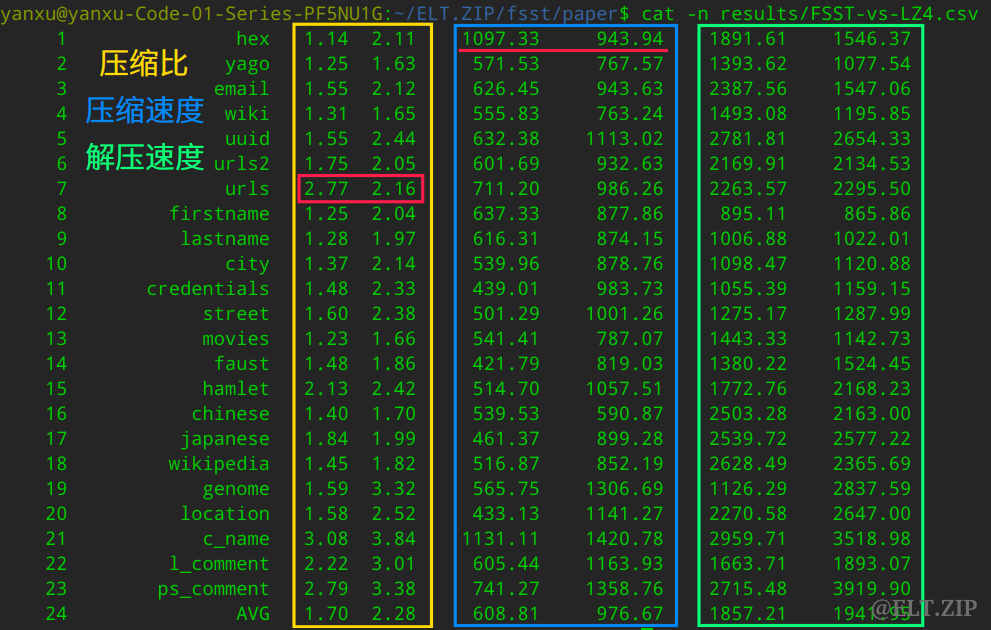
最左侧的一列是各式各样的字符集，另外三个框框分别表示压缩比、压缩速度、解压速度，其中，左侧是 LZ4、右侧是 FSST。不难看出，压缩比方面，FSST 仅在 urls 上较 LZ4 弱了一点；压缩速度方面，LZ4 仅在 hex 上取得了微弱的优势；而解压速度方面，则是二者互有胜负，可以视作忽略不计。

手动测试