【汇思博SEEK100开发板试用体验】4/应用的设计

本来是想要先试着写一个测试工具，不过今天小朋友问我一个问题 - 第一，第二，第三宇宙速度，是个什么玩意。

我想着，语言解说不直观，那直接整个app，能够根据输入的参数，给出轨道，岂不美滋滋？

网上其他up主，其实已经有视频或者图片，比如 -

不过都是做好的动画，不能调整。
说整就整 -

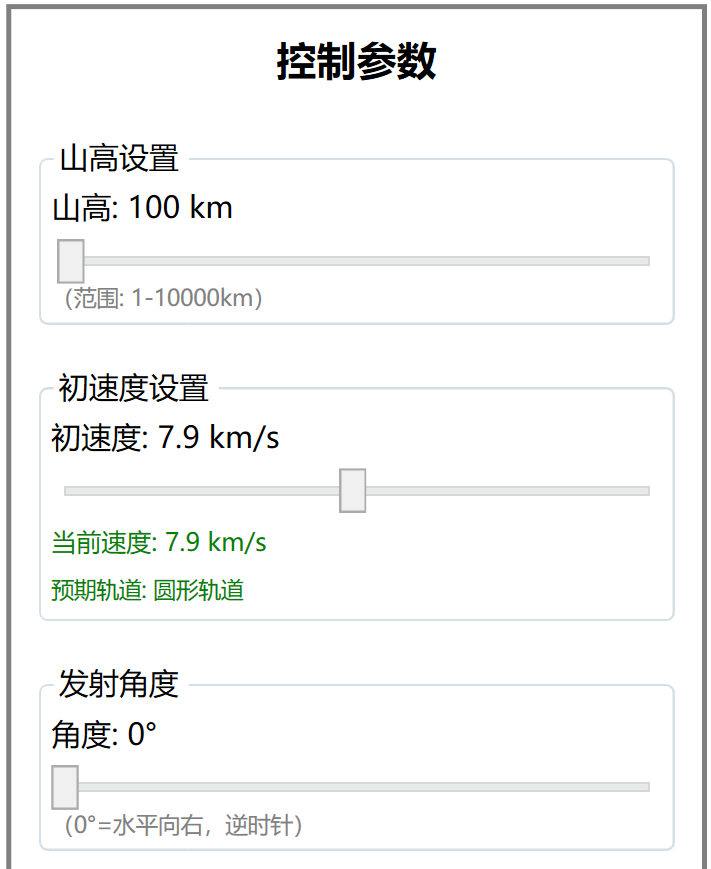
然后，做出的轨道并不理想；查了一下资料，额，好像都是国外的资料。

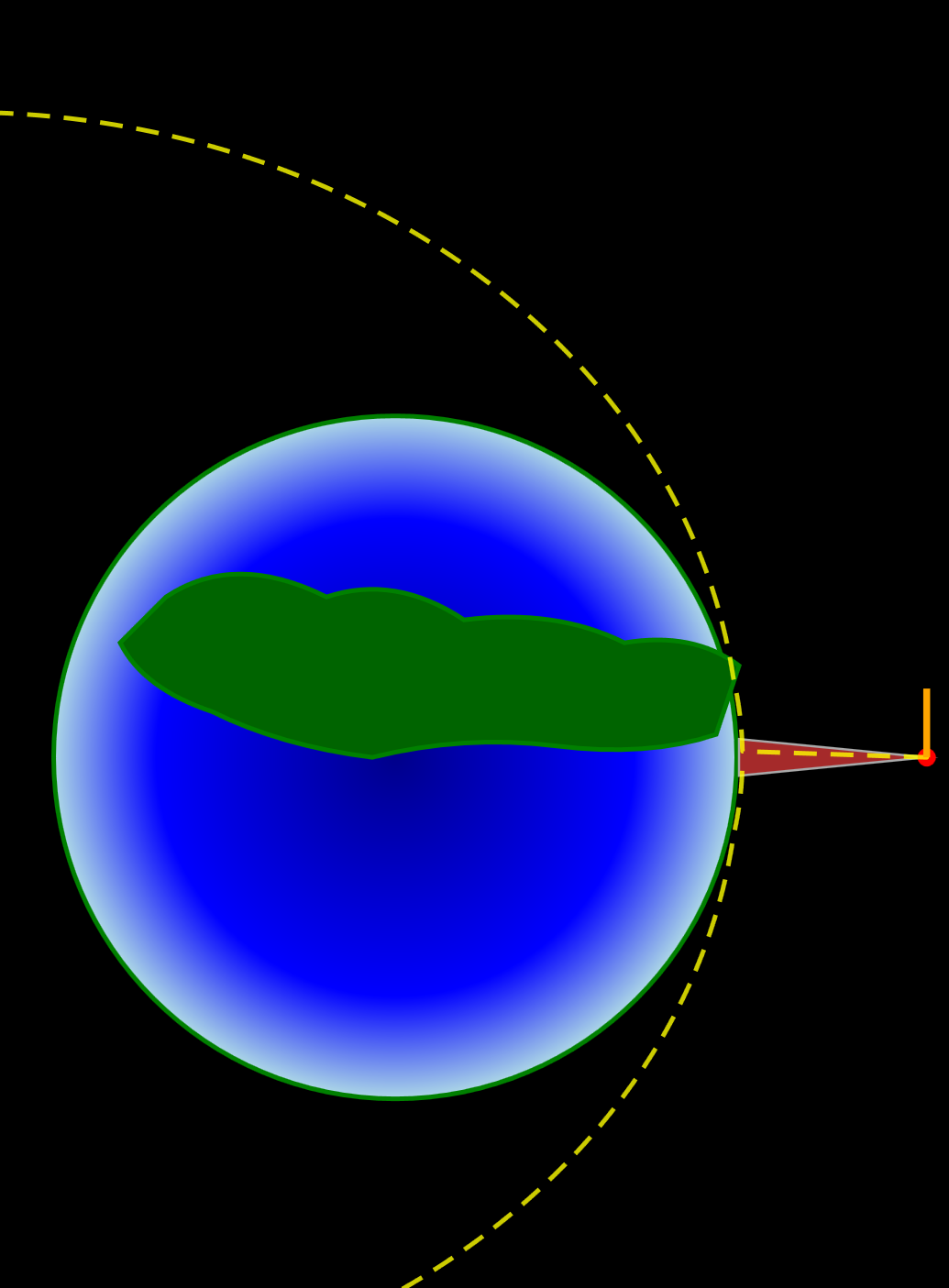
顺便更新了一下自己的知识，原来，平抛运动扔出去的小球，在真实的环境中，跑的原来并不是抛物线，反而是椭圆（的一部分）。

当然了，一些小彩蛋也就不可避免，比如，这个球自己把高度修正到了地平线附近（显示的比例尺问题）... ...

另外，最难的部分，其实是物理（好像还给初中老师了... ...）幸而咨询了大模型君，给出了统一圆锥曲线方程 -

对于速度的各个阶段，有统一的圆锥曲线极坐标方程 - r(θ)= p/(1+ecosθ)，建议​​使用轨道方程通解​​ - 
   步骤1：初始化轨道参数​​
   // 已知量
   Vector2 position = new Vector2(earthRadius, 0); // 初始位置（水平发射）
   Vector2 velocity = new Vector2(0, currentV);    // 初速度（垂直向上）

   double G = 6.674e-11;
   double M_earth = 5.97e24;
   double h = Vector3.Cross(position, velocity).Z;  // 3D叉积获取Z分量
   double epsilon = velocity.LengthSquared()/2 - G*M_earth/position.Length(); // 比机械能
   double e = Math.Sqrt(1 + (2 * epsilon * h * h) / (Math.Pow(G * M_earth, 2))); // 离心率
   double p = (h * h) / (G * M_earth); // 半通径
   ​​步骤2：用统一方程计算轨道点​​
   List<Point> trajectoryPoints = new List<Point>();

   for (double theta = 0; theta <= Math.PI * 2; theta += 0.1)
   {
      double r = p / (1 + e * Math.Cos(theta)); // r(θ)
      
      // 将极坐标(r,θ)转为笛卡尔坐标(x,y)
      double x = r * Math.Cos(theta);
      double y = r * Math.Sin(theta);
      
      trajectoryPoints.Add(new Point(x, y));
   }
   ​​步骤3：特殊处理 v<v1的撞击​​
   当 e<1且初始位置在近地点时，可通过计算​​与地球表面交点​​提前终止轨迹：

   double collisionTheta = Math.Acos((earthRadius - p) / (e * earthRadius));
   if (e < 1 && collisionTheta > 0)
   {
      // 截取 θ ∈ [0, collisionTheta] 的轨迹段
   }

当然了，这里的实际上简化太多了，比如，轨道最难的部分，被我从分段模拟中k出去了，就是亚轨道再入的部分，绕地球多圈飞行，然后掉地上这种。

可能后面会单独出一个版本。

然后又有了更大的野心，为啥不做一个，太阳系内，发射火箭，让小朋友练练手，看怎么徒手扔火箭到火星上去，（虚拟的）比马斯克还早一点登录火星呢？

想想都挺美的。

晚点发app视频。