2. 介绍
在我们的生活中,测试一个机器学习的分类器是否有效,一个标准是统计或者对抗检测(statistically or adversarially detecting)测试样本与训练分布有足够的距离。在许多视觉的分类任务中,可以使用神经网络(DNNs)对样本内(In-Distribution)的类别进行精准分类。
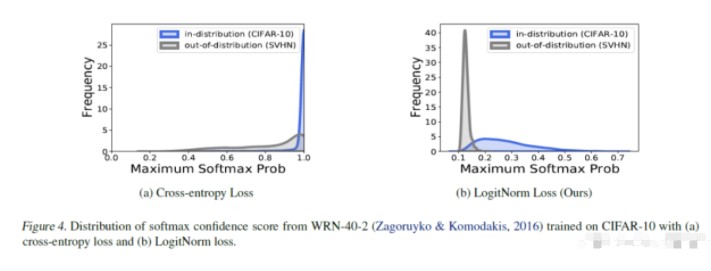
然而,确定预测不确定性仍然是一项困难的任务。而分类中通行的 softmax这一归一化函数,在进行分类的神经网络中会产生“过度自信的结果”。即使若测试样本是ID数据中不存在的类别(Out-of-Distribution),softmax 也会给这个陌生的东西计算出一个概率,而可以产生对数据的over-confidence。在一些场景下,使用此类系统是有风险的,如自动驾驶领域,因为它们可能会导致致命事故。
由于训练数据不能覆盖真实世界中可能出现的各种类别的数据,所以模型的泛化能力有限会在模型部署期间带来一些问题。所以我们希望能够设计一个有效的智能模型,使其能够识别出 OOD 数据,对其进行一系列的干预。
本文介绍一种非常有简洁但有效的工作。在这项工作中,作者表明这个问题可以通过Logit归一化(LogitNorm)来缓解——交叉熵损失的一个简单修复——通过在训练中对Logit执行恒定向量范数。
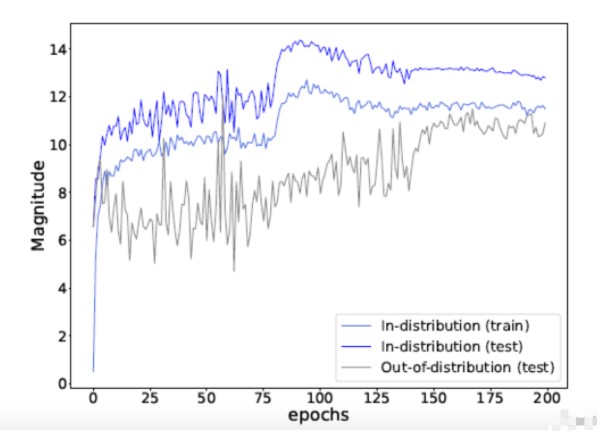
我们的方法的动机是分析logit的规范在训练过程中不断增加,导致过度自信的输出。因此,LogitNorm背后的关键思想是在网络优化过程中去耦输出范数的影响。
朴素的解决方案使用maximum softmax probability (MSP) 来判断样本是OOD还是ID数据。该设定假设OOD数据触发的softmax置信度要比ID数据低。虽然很直观,但现实中却会遇到一个不小的困境。特别是,深度神经网络很容易产生过度自信的预测,即异常高的softmax置信度——即使输入距离训练数据很远,模型经过softmax之后也会给予很高的置信度。所以现有主流的方向倾向于对这个OOD score进行修改。
但是本文指出:迄今为止,community“对过度自信问题的根本原因和缓解措施的理解仍然有限”。所以本文分析了相应的原因,并找到一种非常简洁的方式来解决这一问题。
在这项工作中,作者指出over-confidence的问题可以通过对交叉熵损失函数这一最常用的分类训练目标进行简单修复,从而使其得到缓解。方法很简单,就是在logit向量(即pre-softmax的output)上加上一个normalization。设计的方法 logit normalization(LogitNorm) ,是通过对神经网络的Logit向量的normalization的分析得到的。
论文发现,即使大多数训练样本被正确分类,但softmax交叉熵损失仍然在继续增加logit向量的大小。因此,在训练过程中不断增长的量级导致了over-confidence的问题,尽管其没能提高分类精度。为了缓解这一问题,LogitNorm背后的关键思想是将输出的norm对训练目标及其优化的影响解耦。这可以通过在训练过程中将logit向量归一化,使其具有常数范数来实现。
实际上,我们的LogitNorm损失鼓励logit输出的方向与相应的one-hot标签保持一致,而不加剧输出的幅度。通过使用归一化输出进行训练,该网络倾向于给出保守的预测,并导致ID和OOD输入之间的softmax置信度得分具有很强的可分离性,从而实现比较好的OOD-detection的目的。
3. 方法
论文首先分析了,为什么使用常见的softmax交叉熵损失训练的神经网络会倾向于给出over-confidence的预测。论文的分析表明,大规模的神经网络输出可能是罪魁祸首。
首先把softmax的输出f 写成两部分:


针对这个问题,接着介绍本文提出的方法,其实也非常简单:
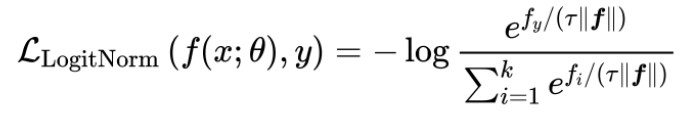
就是输出的logit除以一个模长,再加上一个温度系数. 既然每次模长会累计拉大,那么我们直接根据模长进行归一化就行了。
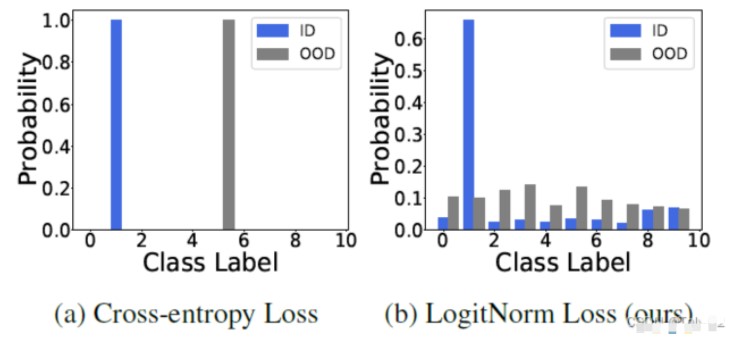
可以看到输出概率的改变十分明显。
对于loss的lower bound:

可以发现,温度系数越大,损失函数下界也随之升高,所以说温度影响优化极限。
4. 实验
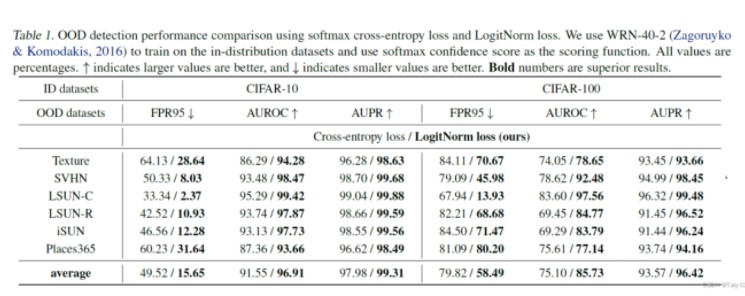
可以看到,在不同的OOD数据集上,把cross-entropy改成LogitNorm的损失函数,都具有明显的性能提升。
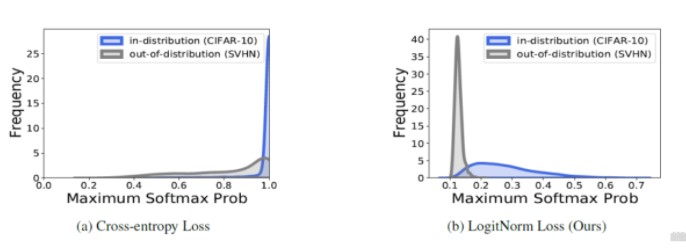
从MSP观察,相对于也具有明显的优势。
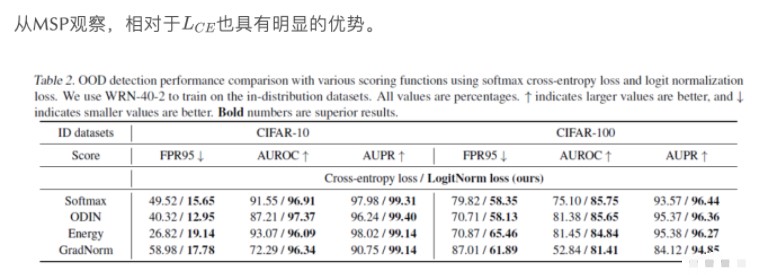
不仅仅是采用MSP这个OOD score来讲有优势,采用ODIN、Energy以及GradNorm等方式同样有非常显著的改进。
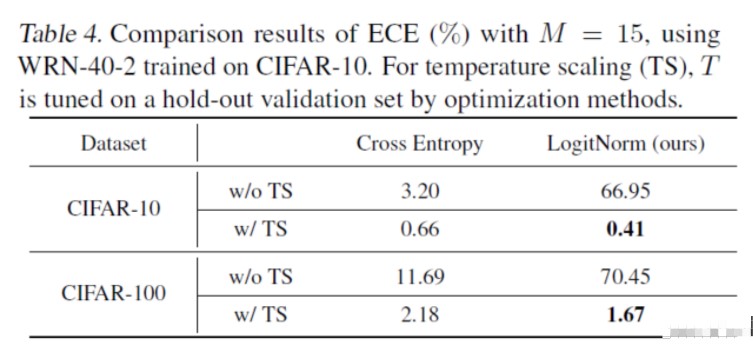
利用ECE这一指标来衡量,可以看到采用合适的标定精度
5. 结论
本文提出一个非常简洁但有效的LogitNorm损失,是对传统cross-entrogy的改进,主要解决神经网络过拟合,同时使得模型矫正能力提升。本文通过理论推导结合实验分析的方式,逐步引出方法,层层递进非常有帮助。
原作者:Garfield
 /9
/9 