衍射级次偏振态的研究

摘要

光栅结构广泛应用于各种光学应用场景，如光谱仪、近眼显示系统、脉冲整形等。快速物理光学软件VirtualLab Fusion通过使用傅里叶模态方法(FMM，也称为RCWA)，为任意光栅结构的严格分析提供了通用和方便的工具。为此，复杂的一维或二维周期结构可以使用界面和调制介质进行配置，这允许任何类型的光栅形貌进行自由的配置。在此用例中，详细讨论了衍射级次的偏振态的研究。

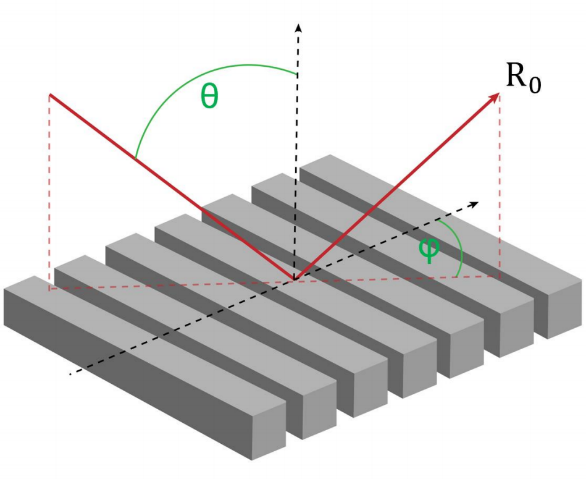
任务说明

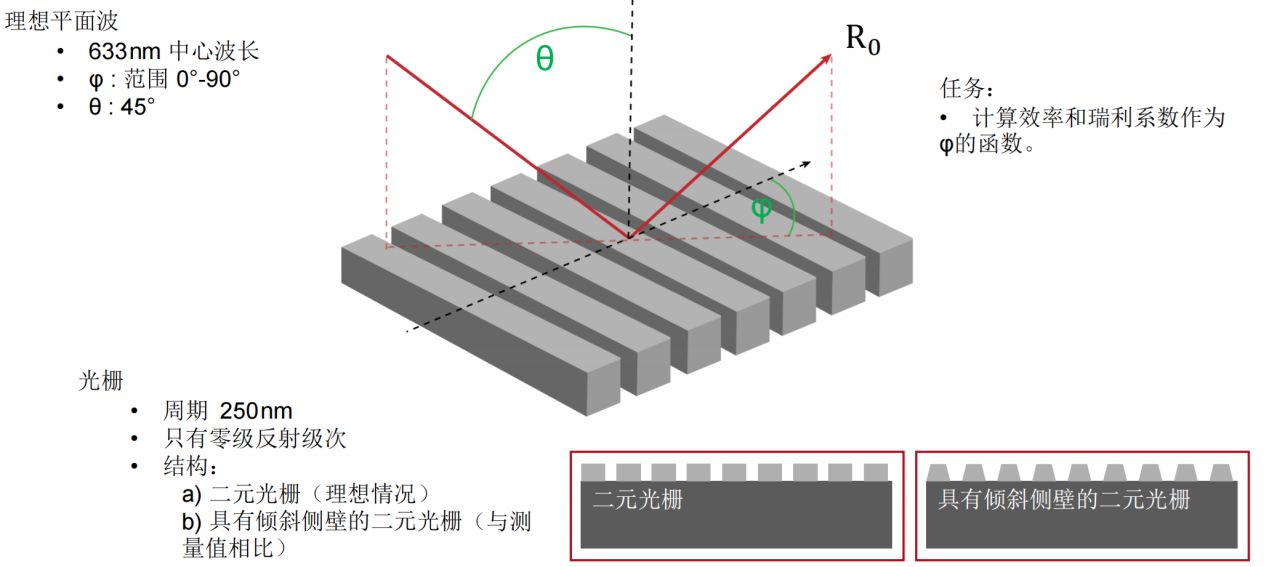
简要介绍衍射效率与偏振理论

某个衍射级次（?）的效率表示有多少的辐射功率被衍射到这个特定的级次中。它是由复数值瑞利系数计算出来的，瑞利系数包含了每个衍射级次（矢量）电磁场的全部信息。瑞利系数本身是由FMM对光栅的特征值问题进行严格分析的结果。

如果在TE/TM坐标系(CS)中给出瑞利系数，则可以计算衍射效率：

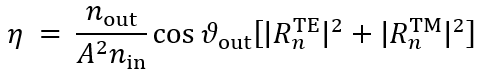
其中，n_in/n_out为覆盖层和衬底层的折射率，ϑ_in/ϑ_out为所分析的阶次的入射角和衍射角。此外，?表示辐射光的振幅。

如果瑞利系数沿?、?和?给出瑞利系数，则必须应用以下方程：

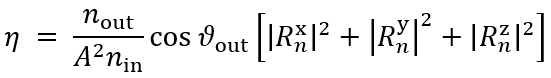
因此，必须考虑所给出的瑞利系数的坐标系。默认情况下，光栅坐标系中为。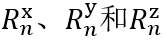

光栅结构参数

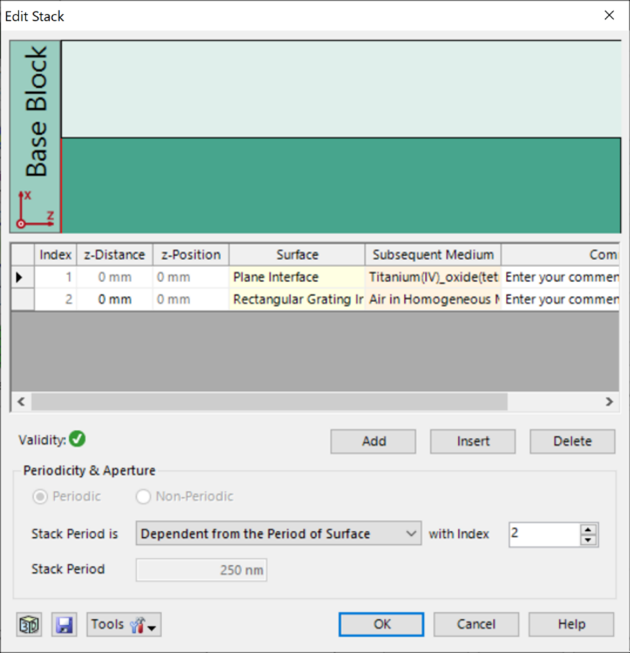
研究了一种矩形光栅结构。

为了简化设置，选择光栅配置，只允许零阶(R_0)反射传播。

根据上述参数选择以下光栅参数：

光栅周期：250 nm

填充因子：0.5

光栅高度：200 nm

材料n_1：熔融石英（来自目录）

材料n_2：二氧化钛（来自目录）

偏振态分析

现在，用TE偏振光照射光栅，并应用圆锥入射角（?）变量。

如前所述，瑞利系数的平方振幅将提供关于特定级次的偏振态的信息。

为了接收瑞利系数作为检测器的结果，需要选择光栅级次分析器件中的单个级次输出，并选择所需的系数。

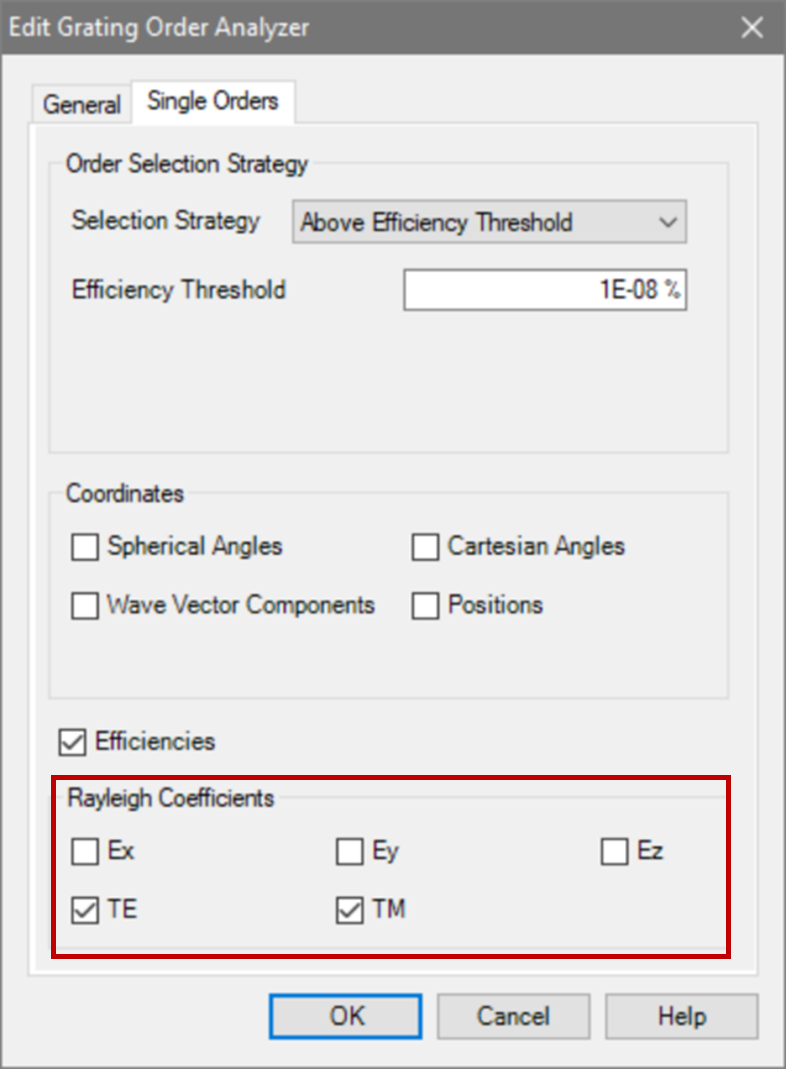
**模拟光栅的偏振态

**

瑞利系数现在提供了偏振态的信息：

在圆锥入射角为0（?=0）时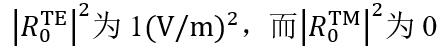，。这说明衍射光是完全偏振的。

对于?=22°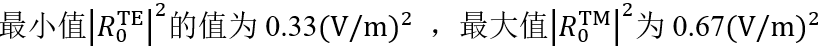，。此时，67%的光是TM偏振的。

对于?>50°，系数接近为常数，因此偏振态也是常数。

Passilly等人更深入的光栅案例 。

Passilly等人的工作研究并优化了亚波长光栅下衍射光谱的偏振态，以获得不同状态之间的高度转换。

因此，他们将模拟结果与制作样品的测量数据进行了比较。

光栅结构参数

在本文中，研究了两种不同的制备光栅结构。

由于加工造成的光栅的理想二元形状的一些偏差是可以预料的，而且确实可以观察到：在基板和侧壁上存在不完全平行的欠刻蚀部分。

由于缺少关于制作结构的细节，我们将其简化为VirtulLab Fusion中的模拟。

但是如果有可用数据，就可以详细分析光栅的复杂形状。

光栅#1——参数

假设侧壁倾斜为线性。

忽略了衬底中的欠刻蚀部分。

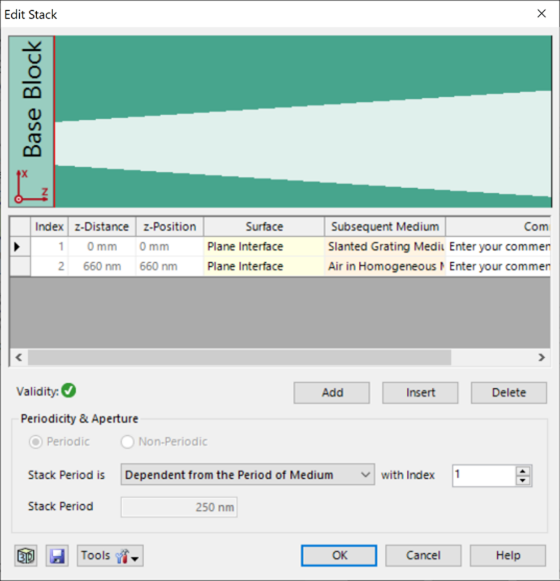
为了实现光栅脊的梯形形状，采用了倾斜光栅介质。

光栅周期：250 nm

光栅高度：660 nm

填充因子：0.75（底部）

侧壁角度：±6°

n_1：1.46

n_2：2.08

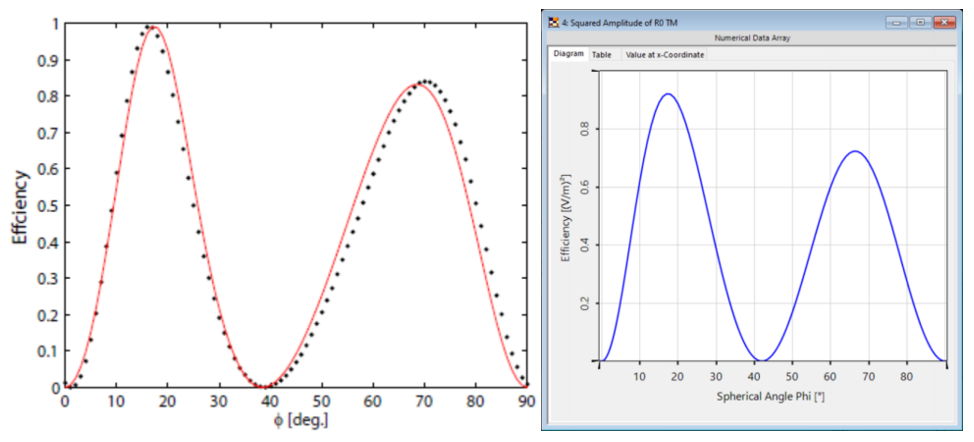
光栅#1——结果

这两幅图对比之下匹配度很高，特别是图表的趋势。

与参考文献相比，仿真中光栅结构进行了简化，存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据，这种简化是必要的。

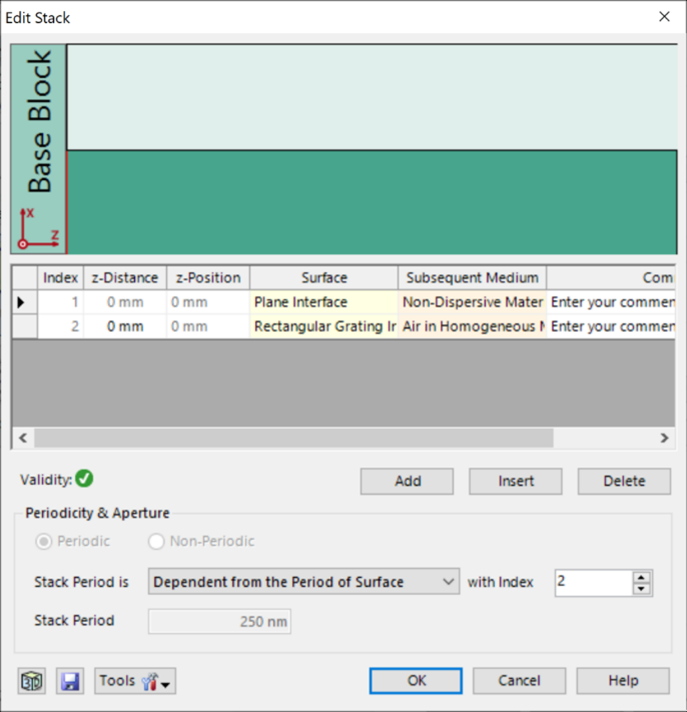
光栅#2——参数

假设光栅为矩形。

忽略了衬底中的欠刻蚀部分。

矩形光栅足以表示这种光栅结构。

光栅周期：250 nm

光栅高度：490 nm

填充因子：0.5

n_1：1.46

n_2：2.08

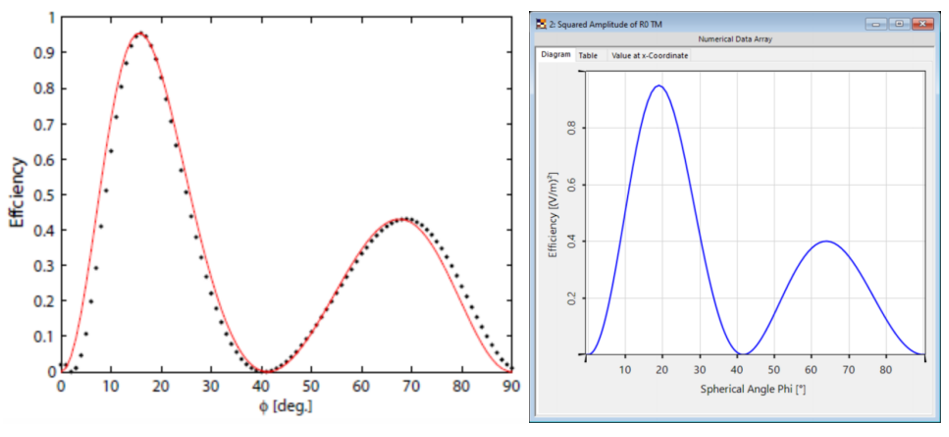
光栅#2——结果

这两幅图对比之下再次显示出非常好的匹配度，特别是图表的趋势。

与参考文献相比，仿真中光栅结构进行了简化，存在一些小的偏差。由于缺乏关于实际的更详细的光栅结构的数据，这种简化是必要的。