电阻器的等效电路与高频无感电阻的性能

电阻器的结构比较简单，但在高频情况下，不能简单地把电阻器看成只是一个电阻分量的理想元件。电阳器实际上是由许多电阻、电感和电容分量组成的复杂阻抗系统，电阻只是其中的一个主要成分。因此必须研究电阻器的直流等效电路、高频等效电路和集肤效应及介质损耗对阻值的影响，并分析研究其性能表现。

EAK设计高频无感电阻

一、直流等效电路

(1)电阳体的电限R。

(2)电阳体与引出线之间的接触电限R。

(3)绝缘基体的并联电阻R!和保护层的并联电阻R"为了简化起见，可用一个绝缘分路电阻R;来代替这两个绝缘分路电阻。见图2-11。

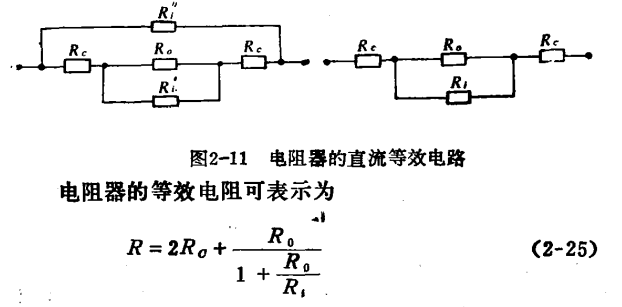
刻螺旋槽的薄膜电阻器，相邻导电带之间的电压降都集中在绝缘槽上，相当于绝缘电阻减小了t/a倍,t为刻槽螺距:g为绝缘槽宽度，使绝缘电阻的影响增大，此时等效电阻可表示为:

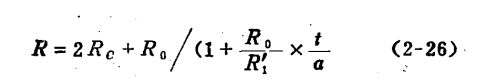
在常温下，如果电阻值不超过10°欧，绝缘电阻的影可忽略不计。当温度很高时，绝缘电阻可能降低很多，应注意它对总电阻的影响。对于高阻值电阻器，当电阻体的阻值R。与绝缘电阻R;相接近时，应注意绝缘电阻的影响。接触电阻R,在电阻系统中的影响比较大。接触电阻影响电阻器的稳定性、温度系数及电流噪声。为了减少接触电阻的影响，应使引线结构与电阻体作紧密的配合，或在电阻体与引线结构之间涂敷低电阻的接触层。采用与基体热胀系数相匹配的金属引线帽。

二、交流等效电路

在频率比较高时，必须考虑电阻器所具有的无功分量的影响。因此，要考虑以下各分量。

(1)电阳体单位长度的分布电感工

(2)电阻体单位长度的分布电容C

(3)引出线之间的集中电容C。

(4)引出线的电感

考虑前三项，即电阻器本身的分布参量，可把一非线绕电阻器表示如图2-12所示的等效电路。这个等效电路与末端短路的传输线的等效电路相同。电阻器的中央相当于传输线的短路端，电阻器的两半段相当于两根传输线，两个引出端相当于输入端。传输线的有效长度等于电阻器工作长度之半L.j=L/2。

引线之间的电容C。取决于引线帽的大小和引线间相隔的距离通常C。不大于1皮法(PE)。

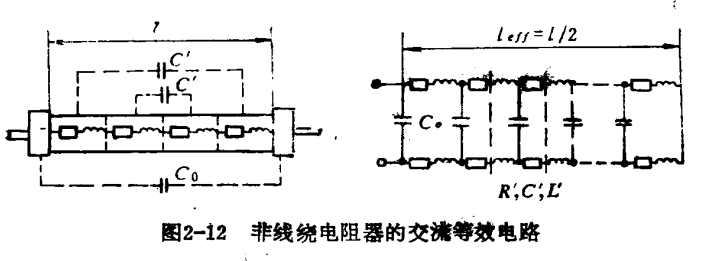
(一)非线绕电阻器的高频性能

可用传输线的理论来分析电阻器的高频性能。

1.高阻值情况

高限值情况下单位长度上的电阻R!比单位长度的感抗ωL'大很多，故可忽略L'的作用。等效电路又进一步简化成图2-13(a)。霍威(Howe)假定电阻器单位长度上的分布电容C是均匀的即C'为常数，并对这个传输线进行分析

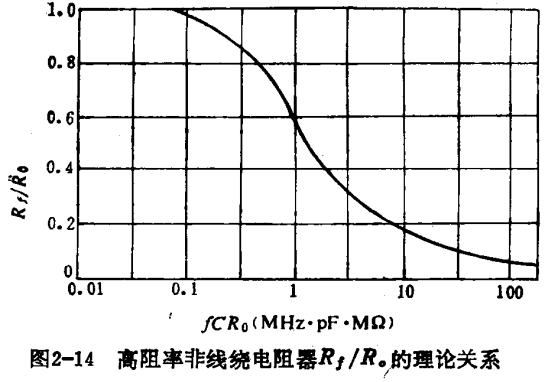
计算，频率为/时电阻器的高频阻值R;与直流阻值R。之比的关系式为:

可把传输线看成一个R;与C，并联的等效电路如图2-13:(6)所示。R;/R。是fCR,的函数，根据(2-27)式可绘制关系曲线，如图2-14所示。

可见，当fCR.≤0,1时，R;IR与频率无关，并日R，R.;当/GRD0,1时，R;将随频率的增高而逐渐减小。

2.低阻值情况

低阻值电阻器，R'较小，如果満足 R'≈∞L'和R'<1/oC'条件，则分布电容的作用可以忽略，只需考虑分布电感的作用。图2-12所示的等效电路可简化成只包含R'和的等效电路，如图2-15所示。将此等效电路进一步简化成集总参数R。-R'1.和L='。,相串联的等效电路,如右侧所示。电阻器的阻抗为：

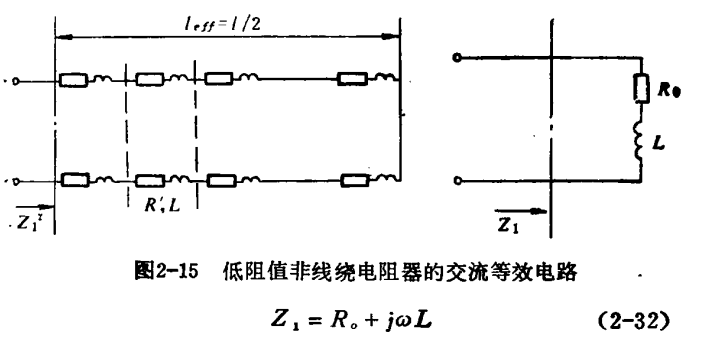
阻抗呈感性，其电阻部分为R。，与频率无关，电抗部分随频率升高而增大。

当频率低而满足R'>∞L'时，可将感抗略去不计，把电阻器看作阻值为R。的纯电阻。若∞工'≤0.1R'，再设低阳值电阻器不刻槽，工'可用公式(2-28)计算，于是得到条件为

EAK厚膜无感电阻

(二)线绕电阻器的高频性能

一般的线绕电阻器，其绕组具有较大的电感和电容，所以在近似条件下，可以将电感和电容看成是集总参数，如图2-16所示的等效电路。

图2-16线绕电阻器的交流等效电路此电路的阻抗可表示为

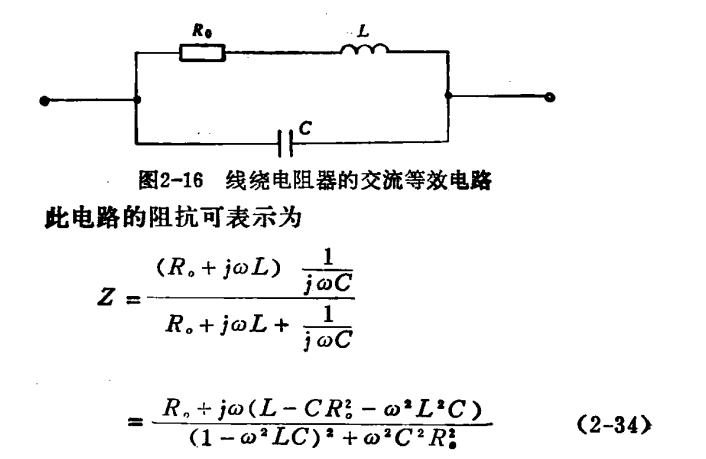
希望时间常数很小，电阻器呈纯阻性，这对脉冲应用是很重要的。适当调整卷绕方法，使时间常数工相补偿，而达到:=0是最佳结果。

EAK线绕高频无感电阻