DSP实验箱操作教程：4-8 快速傅立叶变换（FFT）算法（LCD显示）

4-8 快速傅立叶变换（FFT）算法（LCD显示）

4-8 快速傅立叶变换（FFT）算法（LCD显示）

实验目的

本次教程是基于创龙教仪DSP C6000教学实验箱：TL6748-PlusTEB录制完成的。

本节视频的目的是了解FFT的作用，掌握FFT 算法的算法原理、计算量和算法特点，实现FFT算法并在LCD上显示结果。

实验原理

傅里叶变换

傅里叶变换可以将一个信号从时域变换到频域。时域信号在经过傅立叶变换的分解之后，变为了不同正弦波信号的叠加，我们再去分析这些正弦波的频率，可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的，但是如果变换到频域之后，就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。

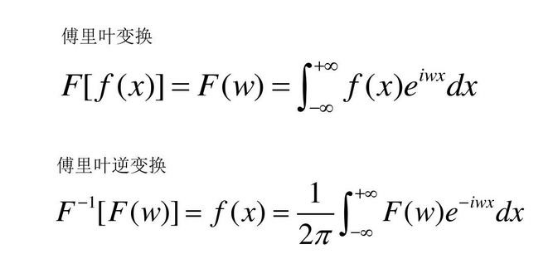
离散傅里叶变换

离散傅里叶变换作为信号处理中最基本和最常用的运算，在信号处理领域占有基础性的地位，如果直接按照离散傅里叶变换的公式进行计算，求出N点X(k)需要N^2次复数运算、N(N-1)次复数加法，当N很大时，运算量是非常大的，这对于实时处理是无法接受的。

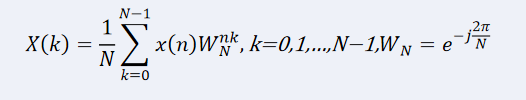
傅里叶快速算法的提出，使傅里叶变换成为一种真正实用的算法。根据傅立叶变换的对称性和周期性，我们可以将DFT运算中有些项合并。在计算机上进行的DFT，使用的输入值是时域的信号值，输入采样点的数量决定了转换的计算规模。变换后的频谱输出包含同样数量的采样点，但是其中有一半的值是冗余的，通常不会显示在频谱中，所以真正有用的信息是N/2+1个点。FFT算法的原理是通过许多小的更加容易进行的变换去实现大规模的变换，降低了运算要求，提高了与运算速度。FFT不是DFT的近似运算，它们完全是等效的，FFT的过程大大简化了在计算机中进行DFT的过程。

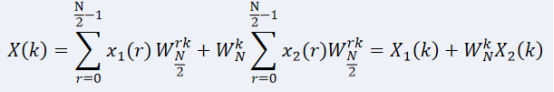
本实验中的FIR算法是基于TI提供的数字信号处理库完成的。 DSPLIB 包含优化的、C语言可调用的通用信号处理例程，用于计算密集型实时应用程序。调用这些例程的运行速度比直接用C语言编写的等效代码快得多，可以缩短应用程序开发时间。实验中使用的是dsplib_c674x_3_4_0_0。

程序使用DSPLIB 的库来进行FFT运算，调用的程序源码和使用说明可以安装DSPLIB后查看。调用的FFT函数中，第一个参数是样本中 FFT 的长度，第二个参数是指向数据输入的指针。第三个参数是指向复杂旋转因子的指针。第四个参数是指向复杂输出数据的指针。第五个参数是指向包含 64 个条目的位反转表的指针。如果样本的FFT长度可以表示为 4 的幂，第六个参数是4，否则第六个参数是 2 。第七个参数是从主FFT开始的样本中的子 FFT偏移索引。第八个参数是样本中主FFT的大小。

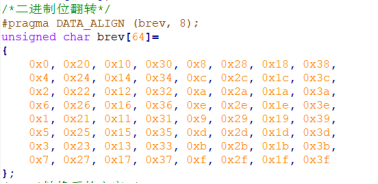
FFT和FFT 逆变换函数中的第五个参数brev是指向包含64个表项的位反转表的指针，因此程序中需要提供64个表项，程序中的位反向表是计算出来的，可以通过代码提前转换的。采用位反转的原因是因为FFT算法的蝶形内部两点交叉使数据以反转的方式输出而不是数字反转顺序。

接下来我们看下二进制位翻转表的原理：

首先确认二进制数的位数，64个数只需要有6位的二进制位数；

接着将二进制数分成两部分，前五位一部分，最后一位一部分；

最后进行二进制翻转，把最后一位放到最高位，剩下的五位进行翻转依次放入。