示波器FFT快速傅立叶变换不会用？看完这篇帖子，我彻底悟了

大多数示波器上都有个FFT功能，也叫快速傅立叶变换，但很多人不了解这个功能是做什么用的，百度以后又会遇到满屏的高数公式，看得一头雾水，继而以放弃告终。

先来看看百度百科对FFT的解释：

FFT，即为快速傅氏变换，是离散傅氏变换的快速算法，它是根据离散傅氏变换的奇、偶、虚、实等特性，对离散傅立叶变换的算法进行改进获得的。

这段冗长而又虚虚实实的文字，看完是不是头都大了？别着急，今天小麦就带大家简单的了解下什么是傅里叶变换以及它的功能作用。

温馨提示：本文不会涉及任何数学公式，目的只在让大家能理解傅里叶变换表达的是什么，至于怎么来的，我们不管。

我们先来理解一下傅里叶变换的基本原理：

傅立叶变换认为，任何复杂的信号都是由多个正余弦波叠加而来的。

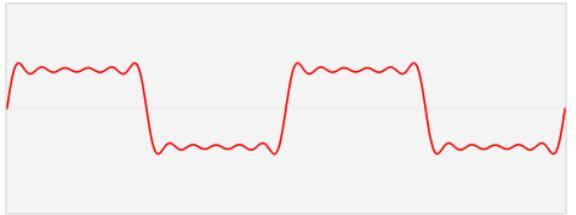
比如这个红色信号，我们就可以看作是多个蓝色正余弦波在垂直向量上的叠加。

大家都知道秤和砝码吧？我们要量物品的重量，就可以用一个一个砝码来标称。这里，这一个个蓝色的正余弦波就是砝码，这个红色的信号就是被测物品。傅立叶变换，就是这杆秤。

通过傅立叶变换，我们可以把这一个个看不见的蓝色信号给抓出来。

再比如，光也是一种波，自然光也是由不同颜色的光叠加而成的。通过傅立叶变换，可以把不同频率的光从自然光中给区分出来。

还有，假设你处在一个嘈杂的环境中，各种各样的声音一起进入你的耳朵，这个嘈杂的声音的声波实际也就是由环境中各种各样声音的声波组合起来的。通过傅立叶变换，可以把不同频率的声音从嘈杂声中给区分出来。

理解频域：

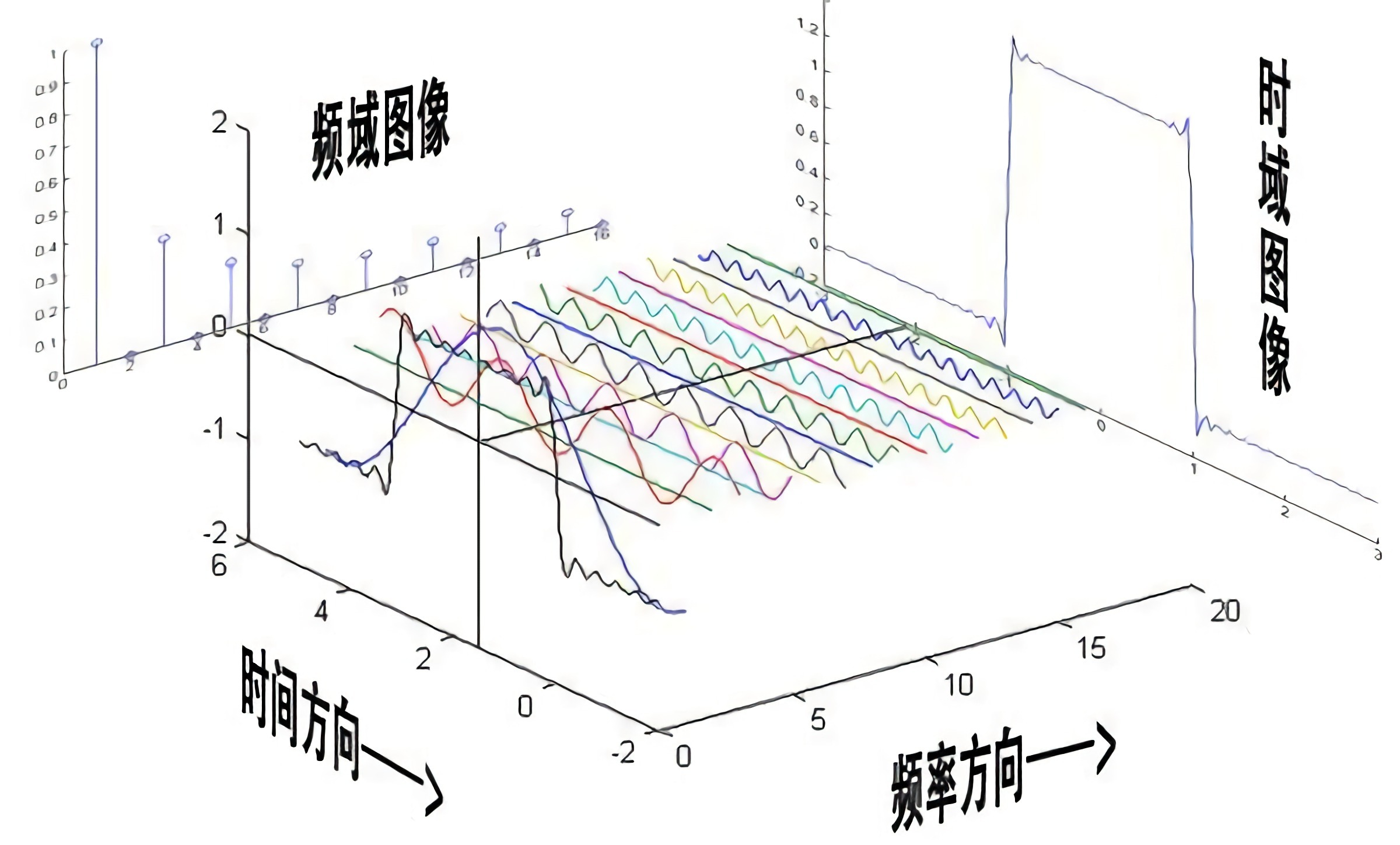
我们活在这个世界，对周围万物的感受，可以说都是在时间轴上的感受。听音乐、画画、跳舞，看着你的孩子一天天长高，观察股市的变化等等，都是建立在时间上变化的，世间万物都随时间不停变化。以时间为参考系去看待这个世界，我们就叫它时域分析。示波器上的信号亦是如此，电压大小随时间变化。这就是时域。

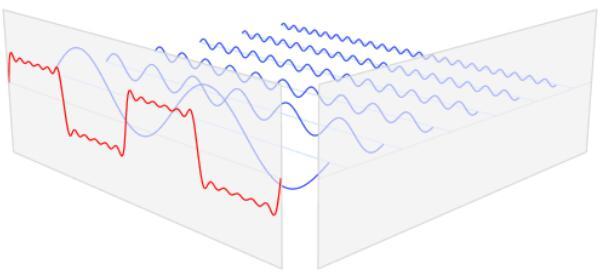
那么，什么是频域呢？顾名思义，频域就是以频率作为参考系去观察的世界。

还记得这个图不?

这里，每个被分出来的蓝色信号都有不同的频率，每个信号有不同的电压值。如果我们把这些信号的频率作为X轴，电压值作为Y轴，就会是下面这样：

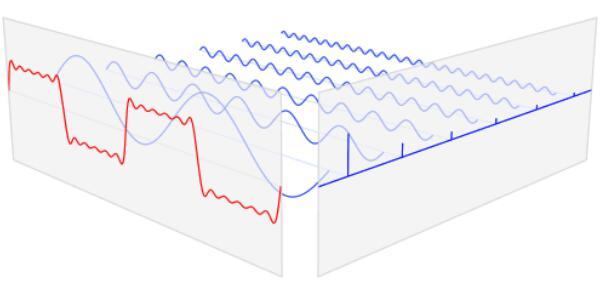
这个图，就是FFT后我们看到的图。这就是频域。

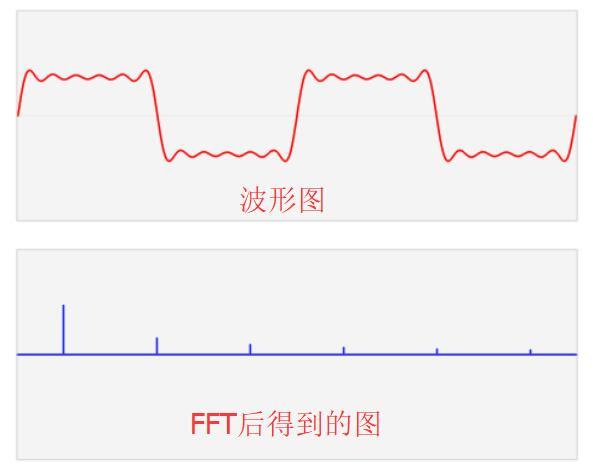
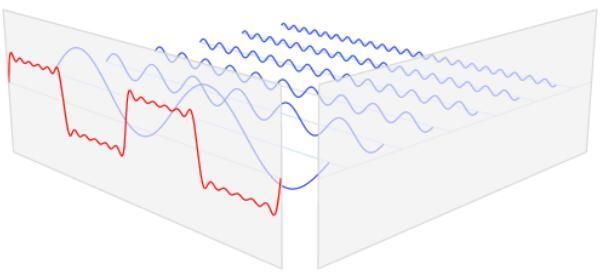
我们上面所学全部汇成一个图，就是下面这样：

示波器实操测量：

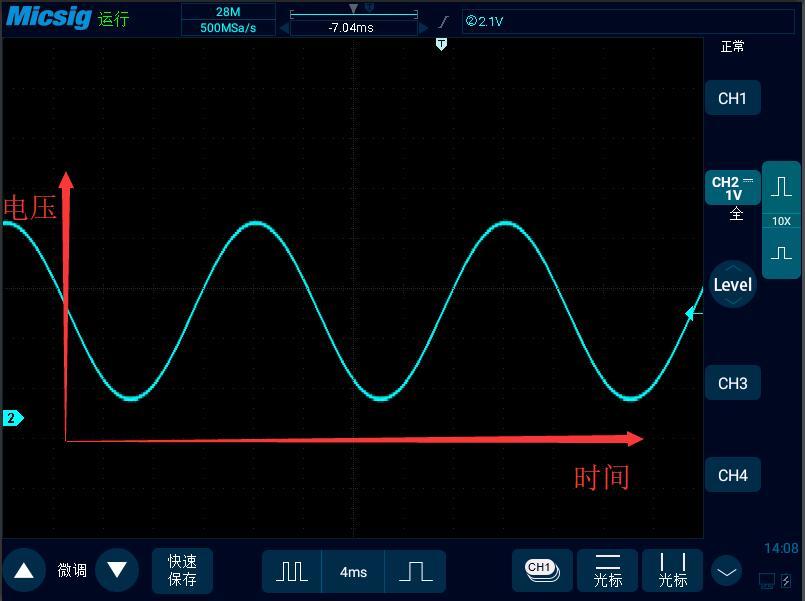
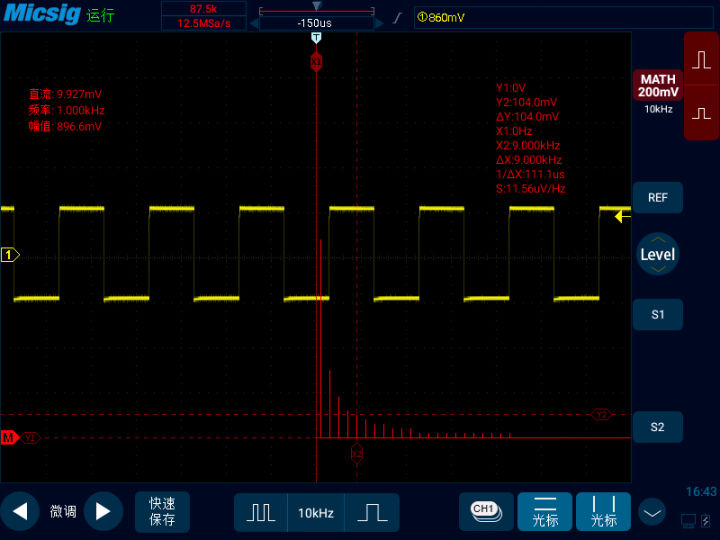
下面这个信号是示波器的校准方波信号，我们打开FFT功能可以看到这个信号的频谱图。

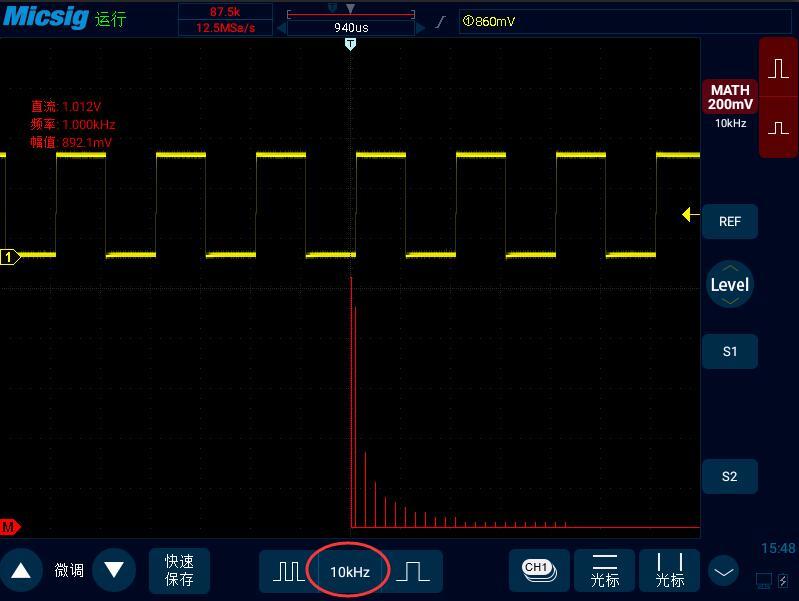
此时，横坐标的时基变成了“频基”，示波器横坐标上一格代表10KHz

纵坐标依然还是代表电压值。

我们打开光标，通过微调，将X1调至0Hz，Y1调至0V，然后我们就可以通过移动X2和Y2来知道某个信号的频率和电压值了。也许你会奇怪，第一条直线0Hz是什么？其实那个就是信号中的直流成分，直流信号的频率是0Hz。我们将通道的耦合方式改成交流，滤除直流信号，你就会发现第一条的直线消失了。

FFT快速傅立叶变换的作用：

FFT就是分析信号的频谱，在物理学、电子类学科、数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学、海洋学、结构动力学等领域都有着广泛的应用。

我们比较熟悉的广播和电视，都需要调频道来观看聆听不同的节目。而频道，就是频率的通道，不同的频道就是将不同的频率作为一个通道来进行信息传输。

示波器的频域分析，在电源调试中也可以起到加速调试进程的作用。在计算机中，图像、文件的压缩也有用到傅立叶变换的计算。我们常用的PS软件里也有很多工具运用到了傅立叶变换的算法。

再比如从某条曲线中去除一些特定的频率成分，也就是滤波，是信号处理中十分重要的概念，也只有在频域才能轻松的做到。我们用的降噪耳机，就是将外界嘈杂声音的频率过滤掉的原理。