pipeline ADC的实现原理及基本结构笔记分享

本文结合文献进一步学习了pipeline ADC的实现原理及基本结构，主要参考了西电、成电和东南的几篇pipelined ADC的硕士论文以及S.H.Lewis的”A pipelined 5-Msample/s Analog-to-Digital Convertor”，以下为个人笔记。

Pipeline ADC的结构图如上图所示，它是由多级相同单元组成的一种ADC结构，每级都进行一次粗量化，输出最终转换出数字量中的几位，第一级为高位，后级输出低位，而总的分辨率，也就是位数就等于所有流水级减掉冗余位后的有效位数之和。

此结构的优越性主要有二：

1.与flash或subranging ADC相比，它的面积更小，功耗更低，这是由于此种结构需要的器件数与分辨率是线性关系，需要更高的分辨率只需要再添加更多流水级，而另两种类型若想要更高分辨率，比较器的数量呈指数上升。

2.流水线结构顾名思义，与流水线CPU相似，每个子级都是并发执行的，当第一级在量化此刻输入的数据时，第二级正在量化上个周期输入的数据，以此类推，这样一来就将ADC转换速度与分辨率独立开来，无论有多少个子级多少位的分辨率，数据都是连续输入连续输出的，相邻数据仅相差一个周期。

接下来简述单个子级的结构及原理。假设单级的分辨率为n，它由S/H电路、n位的子ADC、n位的子DAC、减法器以及乘法器构成，一般也将n位的子DAC、减法器以及乘法器统称为MDAC（multiplying DAC）。

首先， S/H电路采样并保持输入电压，输送给子ADC，子ADC进行n位的粗量化，输出高n位的数字量，之后将量化出的n位数字量再经过一个n位子DAC得到粗量化出的模拟量，将实际输入的模拟量减去这个粗量化出的模拟量，得到的值为剩余的需要继续进行量化的模拟量，称为残差或余差(residue)，之后为了后级能够继续使用相同的子级进行量化，需要将这个残差放大到满量程上，放大倍数为2n。

这里使用数字量来代替模拟量进行理解会更加容易。需要注意，一般对于pipelined ADC来说，输出的数字量0代表负的权重，1代表正的权重。举个简单的例子，假设整个ADC的分辨率为6位，输入所对应的数字量D正好为6’b101101，首级为2位，理想情况下，首级将转换出10这个数码，转换之后剩下待转换的量用数字量表示为6’bzz1101，这里用z表示权重为0，那么为了使用一致的子级结构进行转换，需要将这个值向左移两位，对应于算数运算就是乘以4，即乘以22，之后再送入下一级进行量化，得到11，求出残差乘以4送至下一级，以此类推。

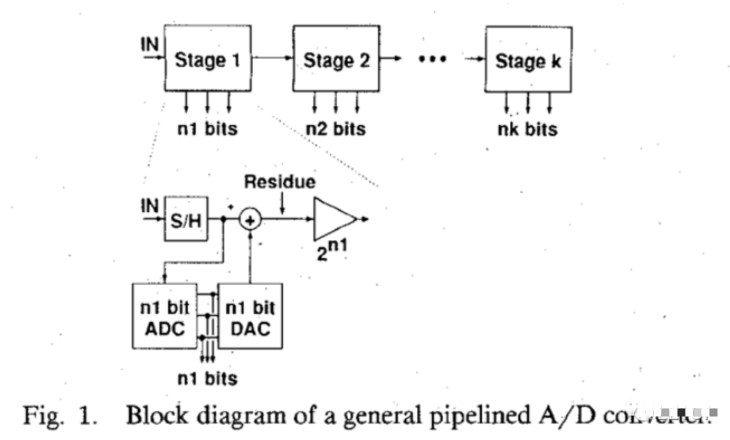
2-bit单级的输入输出特性如下图所示，对应于00、01、10、11四个范围，当输入小于0时，说明最高位必须为0，输入大于0时，最高位必须为1，而当输入小于-VREF/2时，次高位也必须为0（考虑0100000…这个量，它只能逼近-VREF/2而无法小于），其他区间类似可得。比较器判决电压为-VREF/2、0、VREF/2。

那么就可以得到每一输入区间对应该级的子DAC转换出的量，分别为-3/4 VREF、-VREF/4、VREF/4、3/4 VREF。

简单分析动态过程，当Vin = -VREF时，对应Vout = 4 * (-VREF – (-3/4 VREF)) =-VREF。随着Vin增加，转换出的数码为00不变，因此Vout随Vin正比例增加，斜率为级间增益4，当Vin越过第一个判决电压-VREF/2，转换出数码跳变为01，Vout也跳变到-VREF，注意这里也体现出了级间增益将残差放大到满量程的效果，Vin继续增大，Vout依旧是以4为斜率正比例增加，之后的区间类似。

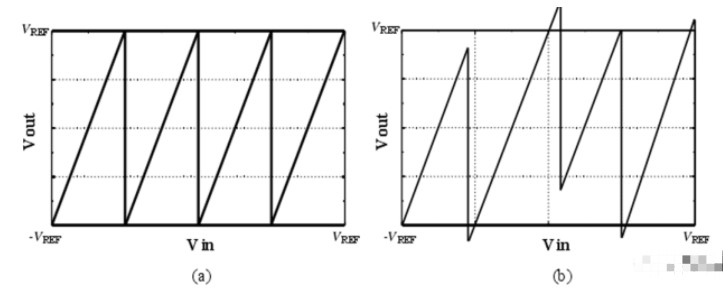
我们注意到，如果子ADC中比较器的判决电压存在偏移，如(b)图所示，就会引入误差，导致误码甚至失码的现象。然而，在MDAC是理想的的情况下，如果这个错误的残差输出没有超过下一级的量程，实际上这个模拟量的信息还是完整地被保存下来了，因此，如果提高下一级的量程，就可以对这个溢出的残差进行转换了。

这里的解释不够准确，感兴趣的朋友可以去看我的笔记(二)

实际上，在pipelined ADC中通常采用数字校准技术，通过使用冗余位，来对易错区间进行单独划分。其原理与提高量程有异曲同工之妙。以下对此技术进行简要解释。

为简单起见，考虑一个1位的流水级，采用了0.5位冗余的输入输出特性曲线如下图所示。可以看到，对应于未加入冗余位的结构，它多出了一个转换区间，包含00、01、10三个区间，其中高位为有效位，而低位是冗余位，高位的权重为VREF/2，低位的权重为VREF/4，有意思的是，该级有效的权重就是VREF/2，多出来的VREF/4权重的位却被保留下来输送给下一位了。观察原来的错误源头，当输入接近判决电压0时，若判决电压存在偏移，输入会被误判到另一个数字输出的区间，产生误码，同时输出余差超出下级量程，那么如果将接近判决电压的部分区域再分出一个区间，认为此区间容易出错因此不加以判断，留到后面再进行判断，就可以避免出现错误的现象了。若想要多划分出区间，就需要增加该级的位数，这也就是冗余码的原理。

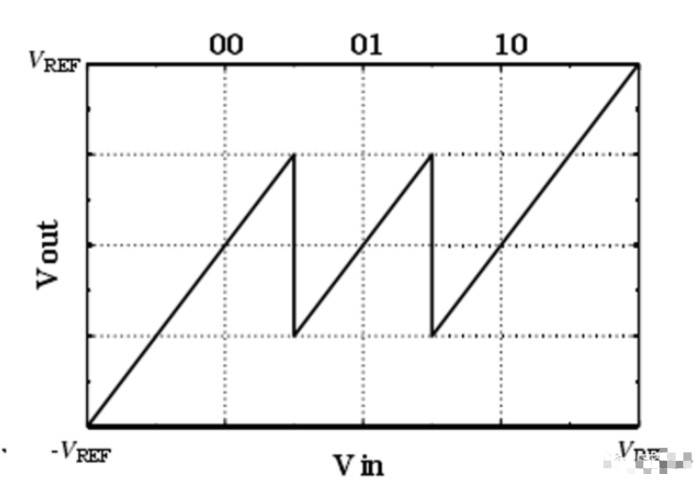
需要注意的是，冗余码的权重实际上是下一级有效码的权重，那么用该级冗余码与下一级有效数码相加，得到的进位就是该级的纠正码，留下的和就是下一级的结果。实际上，所有流水级的结果将冗余码错位再相加就得到了正确的转换结果，将比较器判决电压偏移导致的错误消除了。

原作者：778084265