电路小知识 | 交流电路复数的基础知识以及相位差和电抗的计算

深入解析交流电路基础：波形与特性详解

在上一篇文章中深入解析交流电路基础：波形与特性详解我们给大家分享了波形与特性，本篇继续给大家分享交流电路的计算知识！

复数的应用

复数的基础知识和应用

复数由实部和虚部组成，通常表示为“a+bj”。其中a是实部，b是虚部。复数j是虚数单位，具有“ｊ ^2^ =-1”的性质。

复数也可以通过极坐标形式来表示。在极坐标形式中，复数由振幅和相位角表示。极坐标形式以如下公式表示：

(z = A \cdot e^{j\theta})

其中，A表示幅值，θ表示相位角，j表示虚数单位。

什么是阻抗？

在交流电路中，阻抗是确定电流和电压关系的关键要素。阻抗的计算涉及到电阻、电感和电容的组合，可以认为阻抗是用来确定交流电路中电流和电压关系的复杂电阻。

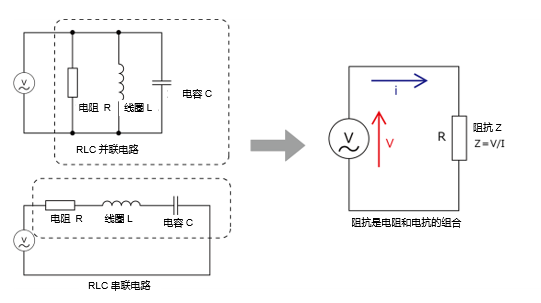
阻抗的计算

阻抗通常用复数表示，由实部（电阻）和虚部（电抗）组成，公式如下：

(Z = R + jX)

其中，Z是阻抗，R是实部（电阻），X是虚部（电抗），j是虚数单位。

电阻

电阻是直接控制电流和电压关系的元件。电阻值（R）用电压（V）和电流（I）之比来表示，适用欧姆定律。

(V = I \times R)

电阻会影响功率损耗和信号的衰减，表示交流电路中的能量损耗。

电阻的阻抗是电阻本身，取决于电阻值。阻抗与电阻的单位相同。

(Z_R = R)

电感

电感取决于线圈和绕组的形状，是导致交流电路中电流延迟的因素。电感值表示电流变化时会感应到电压。因此，电流急剧变化时电压上升，电流缓慢变化时电压下降。

线圈的阻抗由线圈的电感值（L）和角频率（ω）表示，公式如下：

(Z_L = j\omega L)

其中j是虚数单位。

电容（Capacitance）

电容（Capacitance）也称为“电容器（Condenser）”，具有存储电荷的能力。电容值（C）表示电压变化时存储的电荷量。当电压急剧变化时释放电荷，当电压缓慢变化时提供电荷。

电容器既可用于直流电路，也可用于交流电路。在直流电路中，电容器负责存储电荷并提供能量，在电路的稳定性和信号整流方面发挥着重要作用。而在交流电路中，电容表示取决于频率的电抗，在改变信号相位差方面发挥着重要作用。

其基本结构是在两个导体（通常是金属板）之间夹着电介质（绝缘体）。电介质积蓄电荷，积蓄的电荷被作为电场能存储起来。电容器的电容量（电容值，C）表示可以存储的电荷量，用“法拉（F）”表示。

电容器的阻抗由电容器的电容量（C）和角频率（ω）表示，公式如下：

(Z_C = \frac{1}{j\omega C})

相位差和电抗的计算

在交流电路分析中，相位差和电抗是很重要的概念。相位差表示波形的时间偏移量，电抗表示线圈、电容器等组件的阻抗。

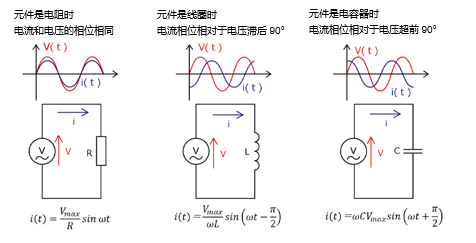
相位差产生的原因及其影响

相位差是因为线圈（Inductor）和电容器（Capacitor）对交流信号的响应不同，并具有取决于频率的电抗而产生的。

这种相位差对电路工作具有以下的影响，因此在交流电路的设计和分析过程中，管理和调整相位差是很重要的工作。

功率传输和损耗：

如果没有相位差（相位为零），电流和电压将同时达到峰值。这可以最大程度地传输功率并最大程度地减少损耗。而当产生相位差时，电流和电压的峰值会有偏移，这可能会降低功率传输效率。当存在相位差时，电流和电压波形会发生偏移，从而会产生不必要的能量损失——无功功率（Reactive
Power）。

电路稳定性：

当产生相位差时，就会发生谐振，即在特定频率处振动最大的现象。当谐振与相位差结合时，电路的响应就会发生变化。另外，电路的特性在不同频段可能会有波动。

在反馈电路等相位是重要因素的电路中，相位差的变化有助于电路的稳定性。

相位差的计算

相位差表示在交流电路中电流和电压的波形随时间偏移的程度。通过弧度来计算相位差是广为使用的方法。

角频率的计算：

通常使用频率f来求角频率ω。

(\omega = 2\pi f)
相位差的计算：

相位差 ϕ 是通过时间t和角频率ω的乘积求得的。

(\phi = \omega t)

例如，当频率f=50Hz时，对应的角频率ω＝2π×50。

如果t=0.01秒，则相位差ϕ＝(2π×50)×0.01。

电抗的计算

电抗是表示线圈和电容器等组件的交流阻抗的指标。电抗通常用“X”来表示。电容器的电抗取决于角频率ω。电容器具有存储电场能和积蓄电荷的特性。当交流信号施加给电容器时，先是电流流动，积蓄电荷；然后电流反向流动，释放电荷。电流的这种延迟是由电容器的电抗造成的，最终会产生电流相对于电压超前的现象。这种超前被视为相位差。

电容器的电抗按下面的公式计算：

(X_C = \frac{1}{2\pi fc})

其中，XC是电容器的电抗，f是频率，C是电容器的电容量。

线圈的电抗也与角频率ω成正比。因此，当频率变化时，线圈的电抗也会发生变化。当交流信号施加给线圈时，线圈内会产生磁场，从而影响线圈的电感值。该磁场的产生和崩溃需要时间，最终会导致电流相对于电压滞后的现象。这种滞后也被视为相位差。

同样，线圈的电抗计算公式如下：

(X_L = 2\pi fL)

其中，XL表示线圈的电抗，f表示频率，L表示线圈的电感。