![]()
![]()
算法 matlab
回帖（1）
2022-1-21 09:57:54
本人以自己的学习过程以及参考别人笔记总结而来，将自己的经验写出来以供大家一起学习，如有错误请多指教---参考《自动控制原理 胡寿松》
案例1：
电机驱动小车的运动：我们理解的小车运动过程中，小车最重要的就是一个电机，电机的输入是pwm输入的电压脉冲输入，有些是电流输入的电机，电机的参数决定了PID的调试效果。假如PWM的输入是100，输出的速度是 y(t)=5m/s，注意的是pwm和输出的速度并非是线性关系，但电机的输出最大速度我们认为在某个场景下是一定的，能达到5m/s。那么我们设定的目标值r(t)=10m/s，那么不管pid如何调节，机子只能在-5m/s到5m/s的值范围内转动，达不到10m/s，也就是说PID算法的调节是本身硬件机械能达到最大值的范围的调节，并非万能的。
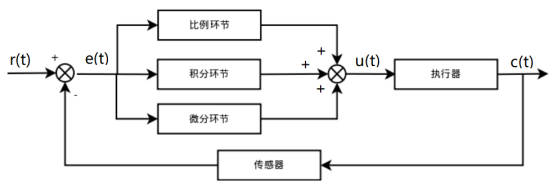
该系统由模拟 PID 控制器和被控对象组成。图中，r(t) 是给定值，y(t) 是系统的实际输出值，给定值与实际输出值构成控制偏差 e(t)： e(t) = r(t) - y(t)，由光电码盘/磁的正负极码盘算出我们的速度，同单位下的速度和速度就有比较意义。通过PID比例积分微分的计算后=pwm的值输入给电机<100%，P、I、D分别为比例（Proportion）、积分（Integral）、微分（Differential）的简写；将偏差的比例、积分和微分通过线性组合构成控制量，用该控制量对受控对象进行控制，称为PID算法。如何计算出实时速度y(t)=一段定时器中断内定时器的外部中断计数值*（一周距离/一周技术值）/定时器时间
1.3 PID整定口诀
参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。
案例2：
煮水和加热电阻丝，我们在陀螺仪的使用中，经常会出现加热一定温度的情况下就不再加热了，温度是滞后的，加热的起始特别慢，等到高温了电阻丝降低PWM降温基本不可能，所以我们使用PID调节时就要考虑到加热的可行性和研究。
案例3：
无人机的位置角度（可以达到的）和转速的比值pid的调节。y与x可以是线性关系/非线性关系，我们接下来要如何调节PID的值界定。
1）比例部分
作用是对系统瞬间产生的偏差进行快速修正，只有 P 时会有静差 。偏差一旦产生控制器立即产生控制作用， 使控制量向减少偏差的方向变化。比例部分的数学式表示是：
Kp * e(t)
注意：Kp是比例系数，Kp越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是越大，也越容易产生振荡，破坏系统的稳定性。故而，比例系数 选择必须恰当，才能过渡时间少，静差小而又稳定的效果。
2）积分部分
作用是消除系统偏差，补偿系统的静差 ，只要存在偏差， 则它的控制作用就不断的增加； 只有在偏差 时， 它的积分才能是一个常数， 控制作用才是一个不会增加的常数。
积分环节的调节作用虽然会消除静态误差，但也会降低系统的响应速度，增加系统的超调量。积分常数 越大， 积分的积累作用越弱， 这时系统在过渡时不会产生振荡； 但是增大积分常数 会减慢静态误差的消除过程，消除偏差所需的时间也较长， 但可以减少超调量，提高系统的稳定性。当Ti 较小时， 则积分的作用较强， 这时系统过渡时间中有可能产生振荡， 不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti 。
3）微分部分
作用是加快调节过程，阻止偏差的变化， 偏差变化的越快， 微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入， 将有助于减小超调量， 克服振荡， 使系统趋于稳定， 特别对髙阶系统非常有利， 它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分， 或在微分起作用之
前先对输入信号进行滤波 。
Td 越大时， 则它抑制偏差 变化的作用越强； Td越小时，则它反抗偏差 变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分常数Td ，可以使微分作用达到最优。
4.2 数字 PID 控制
4.2.1 位置式 PID
由于计算机控制是一种采样控制， 它只能根据采样时刻的偏差计算控制量，而不能像模拟控制那样连续输出控制量量， 进行连续控制。 由于这一特点式中的积分项和微分项不能直接使用，必须进行离散化处理。连续控制是数学研究/真实情况的，计算机采集是离散的，就跟函数和数列一样的关系。
离散化处理的方法为：以T 作为采样周期， 作为采样序号，则离散采样时间 对应着连续时间 ， 用矩形法数值积分近似代替积分， 用一阶后向差分近似代替微分。
上式中，为了表示的方便，将类似于 e(kT )简化成 ek 等。
如果采样周期足够小，则上面的两式的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。
算法的缺点是： 由于全量输出， 所以每次输出均与过去状态有关， 计算时要对 ek 进行累加，工作量大； 并且，因为计算机输出的 对应的是执行机构的实际位置， 如果计算机出现故障，输出的 将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实生产际中是不允许的。
增量式 PID 控制算法可以避免着重现象发生。
4.3 控制器参数整定
PID控制器参数选择的方法很多，例如试凑法、临界比例度法、扩充临界比例度法等。但是，对于PID控制而言，参数选择是用什么方案呢：对于输入目标值而言，我们输入目标值为sin函数值，那么输出的必然存在滞后/超调/达不到峰值的情况，我们将2条曲线数据进行采集对比，就可以知道我们的曲线执行效率是否达到我们的要求。输入目标值也可以是脉冲宽度值，看输出的响应周期进行调节。目标是输出的y(t)是跟x(t)同周期同起点同终点同曲率的曲线。
1）确定比例系数Kp
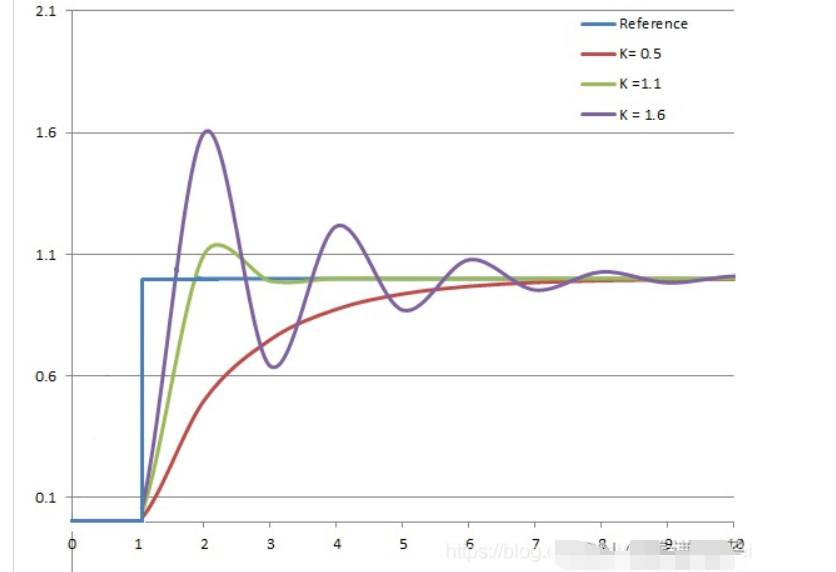
确定比例系数Kp时，首先去掉PID的积分项和微分项，可以令Ti=0、Td=0, 使之成为纯比例调节。输入设定为系统允许输出最大值的60%~70%，比例系数Kp由0开始逐渐增大，直至系统出现振荡:再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp,设定PID的比例系数Kp为当前值的60% ~ 70%。pwm的值不会超过100%，所以kp的值输入可以一个很大的值，看曲线的贴合程度。逐步的二分法靠近一个值。
2) 确定积分时间常数Ti
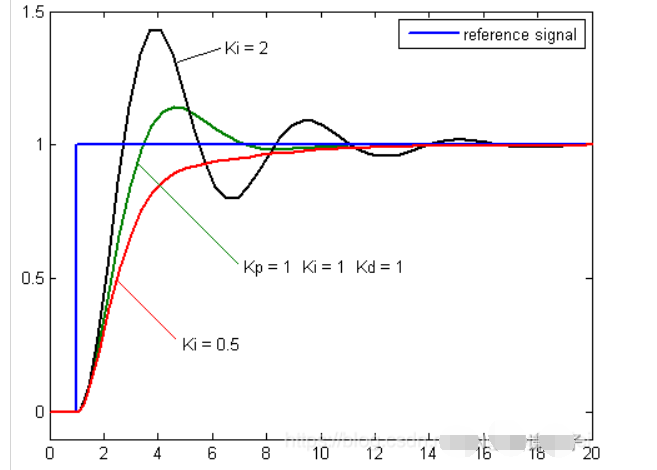
比例系数Kp确定之后，设定一个较 大的积分时间常数Ti,然后逐渐减小Ti,自至系统出现振荡，然后再反过来，逐渐增大Ti,直至系统振荡消失。记录此时的Ti.设定PID的积分时间常数Ti为当前值的150% ~、180%。假定输入目标为1，输出为0，error的值其实是一直在缩小的，Ti最终为稳定一个大值Timax*0，会出现超调的情况，要调节回来即可。
3) 确定微分时间常数Td
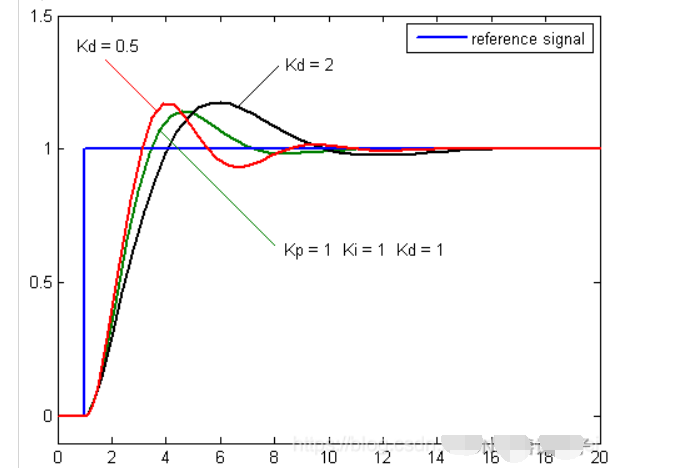
微分时间常数Td一般不用设定，为0即可，此时PID调节转换为PI调节。如果需要设定，则与确定Ti的方法相同，取不振荡时其值的30%。一般电机不用取Td的值，假定输入目标为1，输出为0，error的值其实是一直在缩小的，Td最终为稳定一个小值Timin*0，在目标值附近抖动，一般电机的调节不调节Td的值。
4) 系统空载、带载联调
对PID参数进行微调，直到满足性能要求。
本人以自己的学习过程以及参考别人笔记总结而来，将自己的经验写出来以供大家一起学习，如有错误请多指教---参考《自动控制原理 胡寿松》
案例1：
电机驱动小车的运动：我们理解的小车运动过程中，小车最重要的就是一个电机，电机的输入是pwm输入的电压脉冲输入，有些是电流输入的电机，电机的参数决定了PID的调试效果。假如PWM的输入是100，输出的速度是 y(t)=5m/s，注意的是pwm和输出的速度并非是线性关系，但电机的输出最大速度我们认为在某个场景下是一定的，能达到5m/s。那么我们设定的目标值r(t)=10m/s，那么不管pid如何调节，机子只能在-5m/s到5m/s的值范围内转动，达不到10m/s，也就是说PID算法的调节是本身硬件机械能达到最大值的范围的调节，并非万能的。
该系统由模拟 PID 控制器和被控对象组成。图中，r(t) 是给定值，y(t) 是系统的实际输出值，给定值与实际输出值构成控制偏差 e(t)： e(t) = r(t) - y(t)，由光电码盘/磁的正负极码盘算出我们的速度，同单位下的速度和速度就有比较意义。通过PID比例积分微分的计算后=pwm的值输入给电机<100%，P、I、D分别为比例（Proportion）、积分（Integral）、微分（Differential）的简写；将偏差的比例、积分和微分通过线性组合构成控制量，用该控制量对受控对象进行控制，称为PID算法。如何计算出实时速度y(t)=一段定时器中断内定时器的外部中断计数值*（一周距离/一周技术值）/定时器时间
1.3 PID整定口诀
参数整定找最佳， 从小到大顺序查。
先是比例后积分， 最后再把微分加。
曲线振荡很频繁， 比例度盘要放大。
曲线漂浮绕大弯， 比例度盘往小扳。
曲线偏离回复慢， 积分时间往下降。
曲线波动周期长， 积分时间再加长。
曲线振荡频率快， 先把微分降下来。
动差大来波动慢， 微分时间应加长。
理想曲线两个波， 前高后低四比一。
一看二调多分析， 调节质量不会低。
案例2：
煮水和加热电阻丝，我们在陀螺仪的使用中，经常会出现加热一定温度的情况下就不再加热了，温度是滞后的，加热的起始特别慢，等到高温了电阻丝降低PWM降温基本不可能，所以我们使用PID调节时就要考虑到加热的可行性和研究。
案例3：
无人机的位置角度（可以达到的）和转速的比值pid的调节。y与x可以是线性关系/非线性关系，我们接下来要如何调节PID的值界定。
1）比例部分
作用是对系统瞬间产生的偏差进行快速修正，只有 P 时会有静差 。偏差一旦产生控制器立即产生控制作用， 使控制量向减少偏差的方向变化。比例部分的数学式表示是：
Kp * e(t)
注意：Kp是比例系数，Kp越大，控制作用越强，则过渡过程越快，控制过程的静态偏差也就越小；但是越大，也越容易产生振荡，破坏系统的稳定性。故而，比例系数 选择必须恰当，才能过渡时间少，静差小而又稳定的效果。
2）积分部分
作用是消除系统偏差，补偿系统的静差 ，只要存在偏差， 则它的控制作用就不断的增加； 只有在偏差 时， 它的积分才能是一个常数， 控制作用才是一个不会增加的常数。
积分环节的调节作用虽然会消除静态误差，但也会降低系统的响应速度，增加系统的超调量。积分常数 越大， 积分的积累作用越弱， 这时系统在过渡时不会产生振荡； 但是增大积分常数 会减慢静态误差的消除过程，消除偏差所需的时间也较长， 但可以减少超调量，提高系统的稳定性。当Ti 较小时， 则积分的作用较强， 这时系统过渡时间中有可能产生振荡， 不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定Ti 。
3）微分部分
作用是加快调节过程，阻止偏差的变化， 偏差变化的越快， 微分控制器的输出就越大，并能在偏差值变大之前进行修正。微分作用的引入， 将有助于减小超调量， 克服振荡， 使系统趋于稳定， 特别对髙阶系统非常有利， 它加快了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感，对那些噪声较大的系统一般不用微分， 或在微分起作用之
前先对输入信号进行滤波 。
Td 越大时， 则它抑制偏差 变化的作用越强； Td越小时，则它反抗偏差 变化的作用越弱。微分部分显然对系统稳定有很大的作用。适当地选择微分常数Td ，可以使微分作用达到最优。
4.2 数字 PID 控制
4.2.1 位置式 PID
由于计算机控制是一种采样控制， 它只能根据采样时刻的偏差计算控制量，而不能像模拟控制那样连续输出控制量量， 进行连续控制。 由于这一特点式中的积分项和微分项不能直接使用，必须进行离散化处理。连续控制是数学研究/真实情况的，计算机采集是离散的，就跟函数和数列一样的关系。
离散化处理的方法为：以T 作为采样周期， 作为采样序号，则离散采样时间 对应着连续时间 ， 用矩形法数值积分近似代替积分， 用一阶后向差分近似代替微分。
上式中，为了表示的方便，将类似于 e(kT )简化成 ek 等。
如果采样周期足够小，则上面的两式的近似计算可以获得足够精确的结果，离散控制过程与连续过程十分接近。
算法的缺点是： 由于全量输出， 所以每次输出均与过去状态有关， 计算时要对 ek 进行累加，工作量大； 并且，因为计算机输出的 对应的是执行机构的实际位置， 如果计算机出现故障，输出的 将大幅度变化，会引起执行机构的大幅度变化，有可能因此造成严重的生产事故，这在实生产际中是不允许的。
增量式 PID 控制算法可以避免着重现象发生。
4.3 控制器参数整定
PID控制器参数选择的方法很多，例如试凑法、临界比例度法、扩充临界比例度法等。但是，对于PID控制而言，参数选择是用什么方案呢：对于输入目标值而言，我们输入目标值为sin函数值，那么输出的必然存在滞后/超调/达不到峰值的情况，我们将2条曲线数据进行采集对比，就可以知道我们的曲线执行效率是否达到我们的要求。输入目标值也可以是脉冲宽度值，看输出的响应周期进行调节。目标是输出的y(t)是跟x(t)同周期同起点同终点同曲率的曲线。
1）确定比例系数Kp
确定比例系数Kp时，首先去掉PID的积分项和微分项，可以令Ti=0、Td=0, 使之成为纯比例调节。输入设定为系统允许输出最大值的60%~70%，比例系数Kp由0开始逐渐增大，直至系统出现振荡:再反过来，从此时的比例系数Kp逐渐减小，直至系统振荡消失。记录此时的比例系数Kp,设定PID的比例系数Kp为当前值的60% ~ 70%。pwm的值不会超过100%，所以kp的值输入可以一个很大的值，看曲线的贴合程度。逐步的二分法靠近一个值。
2) 确定积分时间常数Ti
比例系数Kp确定之后，设定一个较 大的积分时间常数Ti,然后逐渐减小Ti,自至系统出现振荡，然后再反过来，逐渐增大Ti,直至系统振荡消失。记录此时的Ti.设定PID的积分时间常数Ti为当前值的150% ~、180%。假定输入目标为1，输出为0，error的值其实是一直在缩小的，Ti最终为稳定一个大值Timax*0，会出现超调的情况，要调节回来即可。
3) 确定微分时间常数Td
微分时间常数Td一般不用设定，为0即可，此时PID调节转换为PI调节。如果需要设定，则与确定Ti的方法相同，取不振荡时其值的30%。一般电机不用取Td的值，假定输入目标为1，输出为0，error的值其实是一直在缩小的，Td最终为稳定一个小值Timin*0，在目标值附近抖动，一般电机的调节不调节Td的值。
4) 系统空载、带载联调
对PID参数进行微调，直到满足性能要求。
举报
更多回帖
