卡尔曼滤波在信号处理方面用的是比较多的,资料也是非常多的,这里就不写了。自适应卡尔曼滤波也有很多文献有相关的介绍,其中用的比较多的有基于Sage-Husa算法实现的。这段时间刚好用到,顺便做了一个,参考了一些网上的程序如:
https://zhuanlan.zhihu.com/p/100074040
基本卡尔曼以及状态和测量方程方面采用了原来程序的一些内容。Sage-Husa部分进行了改进,主程序如下:
close all;
clear all;
N=1000;
% inlitial Kalman Filter
qu=1;
F = [0.0673 0.1553; 1 0];
G = [1 -0.575 ; 0 0];
H = [1 0];
a=randn(1,N)*sqrt(qu);
Q0=diag([qu qu]); %process noise
R0 = 1; %measurement noise
P0=eye(2)*10000;
y=zeros(1,N);
y(1)=a(1);
y(2)=a(2)-0.575*a(1);
for k=3:N
y(k)=0.0673*y(k-1)+0.1553*y(k-2)+a(k)-0.575*a(k-1);
end
y = y+sqrt(R0)*randn(1,N); %add the measure noise
% because the measurement equal the state variable add a noise in one
% dimension, so initiate it with y(1)
X0=[y(1);0];
b=0.8; % parameter of Sage Husa
[X,P]=Sage_HusaKF(F,G,H,Q0,R0,X0,y,P0,b);
% display the result
t=1:N;
figure
subplot(2,1,1);
plot(t,y,'b',t,X(1,:),'--r');
legend('measure','estimated');
title('Measure value and the estimated value');
subplot(2,1,2);
plot(t,y-X(1,:));
title('error');
其中调用的函数Sage_HusaKF如下:
% modified version of Sage-Husa adeptive KF
function [X,P]=Sage_HusaKF(F,G,H,Q0,R,X0,Z,P,b)
N=size(Z,2); %lenght of the measure data in the column
M=length(X0);
X=zeros(M,N);
X(:,1)=X0;
e=zeros(size(Z));
q = zeros(M,1);
Q = Q0;
for k=2:N
Ptemp=P;
X_est=F*X(:,k-1); %计算一步预测估计:X(k/k-1)
P_pre=F*P*F'+G*Q*G'; %一步预测估计的均方误差P(k/k-1)
e(:,k)=Z(:,k)-H*X_est; %计算残差epsilon(k)
K=P_pre*H'*pinv((H*P_pre*H')+R); %k时刻的增益阵
X(:,k)=X_est+K*e(:,k); %k时刻的状态估计X(k)
P = (eye(M)-K*H)*P_pre;% 均方误差矩阵P(k)
% Sage-Husa adeptive KF,这里做了一些修改
d = (1-b)/(1-b^(N));
q = (1-d*b^(k-1))*q +d*b^k*(X(:,k)-F*X(:,k-1));
Q = (1-d*b^(k-1))*Q +d*b^k*(K*e(:,k)*e(:,k)'*K'+Ptemp-F*P*F');
end
end
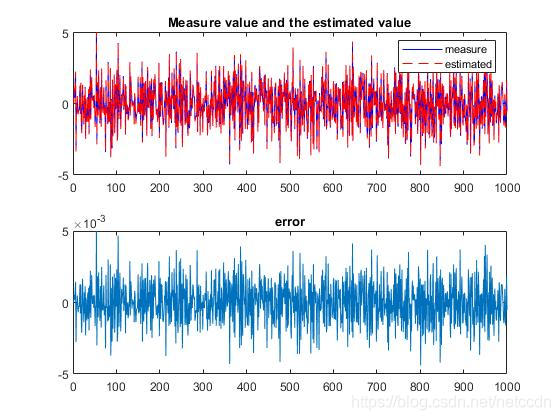
下面是一个仿真结果:
效果基本还可以。
在下面的mathworks网站的“File Exchange”板块也上传一个英文版的,两个版本内容基本一致。
https://www.mathworks.com/matlabcentral/fileexchange/89431-adaptive-kalman-via-a-modified-sage-husa-algorithm
关于q和Q的推导如下图:

需要说明的是基本卡尔曼滤波性能与矩阵P的初值关系很小,改进后滤波性能与P的初值相关性很高,在某些情况下可以较大地改进滤波效果。
另外,该改进方法只对该特定的模型有效,其它的模型,试验过几个,都无效 。
卡尔曼滤波在信号处理方面用的是比较多的,资料也是非常多的,这里就不写了。自适应卡尔曼滤波也有很多文献有相关的介绍,其中用的比较多的有基于Sage-Husa算法实现的。这段时间刚好用到,顺便做了一个,参考了一些网上的程序如:
https://zhuanlan.zhihu.com/p/100074040
基本卡尔曼以及状态和测量方程方面采用了原来程序的一些内容。Sage-Husa部分进行了改进,主程序如下:
close all;
clear all;
N=1000;
% inlitial Kalman Filter
qu=1;
F = [0.0673 0.1553; 1 0];
G = [1 -0.575 ; 0 0];
H = [1 0];
a=randn(1,N)*sqrt(qu);
Q0=diag([qu qu]); %process noise
R0 = 1; %measurement noise
P0=eye(2)*10000;
y=zeros(1,N);
y(1)=a(1);
y(2)=a(2)-0.575*a(1);
for k=3:N
y(k)=0.0673*y(k-1)+0.1553*y(k-2)+a(k)-0.575*a(k-1);
end
y = y+sqrt(R0)*randn(1,N); %add the measure noise
% because the measurement equal the state variable add a noise in one
% dimension, so initiate it with y(1)
X0=[y(1);0];
b=0.8; % parameter of Sage Husa
[X,P]=Sage_HusaKF(F,G,H,Q0,R0,X0,y,P0,b);
% display the result
t=1:N;
figure
subplot(2,1,1);
plot(t,y,'b',t,X(1,:),'--r');
legend('measure','estimated');
title('Measure value and the estimated value');
subplot(2,1,2);
plot(t,y-X(1,:));
title('error');
其中调用的函数Sage_HusaKF如下:

% modified version of Sage-Husa adeptive KF
function [X,P]=Sage_HusaKF(F,G,H,Q0,R,X0,Z,P,b)
N=size(Z,2); %lenght of the measure data in the column
M=length(X0);
X=zeros(M,N);
X(:,1)=X0;
e=zeros(size(Z));
q = zeros(M,1);
Q = Q0;
for k=2:N
Ptemp=P;
X_est=F*X(:,k-1); %计算一步预测估计:X(k/k-1)
P_pre=F*P*F'+G*Q*G'; %一步预测估计的均方误差P(k/k-1)
e(:,k)=Z(:,k)-H*X_est; %计算残差epsilon(k)
K=P_pre*H'*pinv((H*P_pre*H')+R); %k时刻的增益阵
X(:,k)=X_est+K*e(:,k); %k时刻的状态估计X(k)
P = (eye(M)-K*H)*P_pre;% 均方误差矩阵P(k)
% Sage-Husa adeptive KF,这里做了一些修改
d = (1-b)/(1-b^(N));
q = (1-d*b^(k-1))*q +d*b^k*(X(:,k)-F*X(:,k-1));
Q = (1-d*b^(k-1))*Q +d*b^k*(K*e(:,k)*e(:,k)'*K'+Ptemp-F*P*F');
end
end
下面是一个仿真结果:
效果基本还可以。
在下面的mathworks网站的“File Exchange”板块也上传一个英文版的,两个版本内容基本一致。
https://www.mathworks.com/matlabcentral/fileexchange/89431-adaptive-kalman-via-a-modified-sage-husa-algorithm
关于q和Q的推导如下图:

需要说明的是基本卡尔曼滤波性能与矩阵P的初值关系很小,改进后滤波性能与P的初值相关性很高,在某些情况下可以较大地改进滤波效果。
另外,该改进方法只对该特定的模型有效,其它的模型,试验过几个,都无效 。

 举报
举报




 举报
举报

