CIC抽取滤波器MATLAB仿真和FPGA实现(1)
设计理想滤波器目标:1、滤波器在有效频段内纹波满足设计要求。2、抽取或内插处理后在有效频段内不产生混叠。3、滤波器实现简单,需要资源较少。这个文章主要讲CIC理论基础,下个文章讲FPGA实现。
级联积分梳状滤波器又称CIC。这是多速率信号处理中一种结构简单的滤波器,只需要加法器和寄存器即可实现,可以灵活的设置抽取因子和插值因子,并且CIC是一种基于零点和极点相消的FIR滤波器。
CIC是由积分器和梳状滤波器组成。积分器可表示为(太多公式了只能截图发出来)

根据上面的分析可以知道积分器对直流有着无限的的增益,在应用时这是一个不稳定的系统。
梳状滤波器可表示为

单级CIC在不同延时长度时冲击响应的频谱特性MATLAB代码如下:
M=2; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec8=Spec-max(Spec);
%plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
%xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
%legend(‘M=2’,‘M=5’,‘M=7’,‘M=8’);
%grid;
plot(f,Spec2,’-’,f,Spec5,’。’,f,Spec8,’–’);axis([0 1 -50 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘M=2’,‘M=5’,‘M=8’);
grid;
幅频响应如下图:
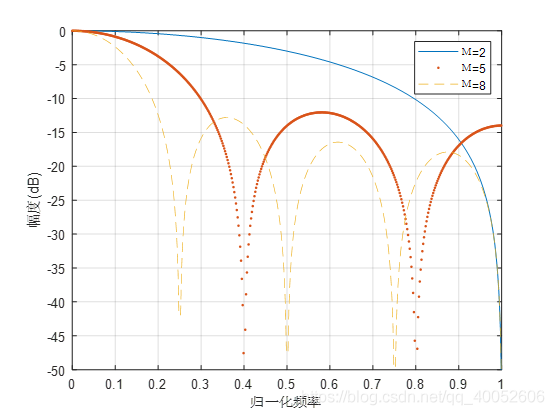

理论计算与上图仿真结果相对应。
然而在实际应用中第一级抑制比太低,可以通过级联CIC的方式得到想要的抑制比。在RM一定的情况下由于级联后传递函数是乘机的关系,因此抑制比是累加的关系,如四级CIC级联后第一旁瓣抑制比在53.84dB。但是增加滤波器级联数目虽然可以解决旁瓣电平衰减减小问题,但是会带来通带衰减较大的问题,并且在实现时会消耗更多的资源。下面是5级CIC级联不同RM的MATLAB代码和频谱特性图
M=2; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec8=Spec-max(Spec);
%plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
%xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
%legend(‘M=2’,‘M=5’,‘M=7’,‘M=8’);
%grid;
plot(f,Spec2,’-’,f,Spec5,’。’,f,Spec8,’–’);axis([0
1 -200 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘M=2’,‘M=5’,‘M=8’);
grid;
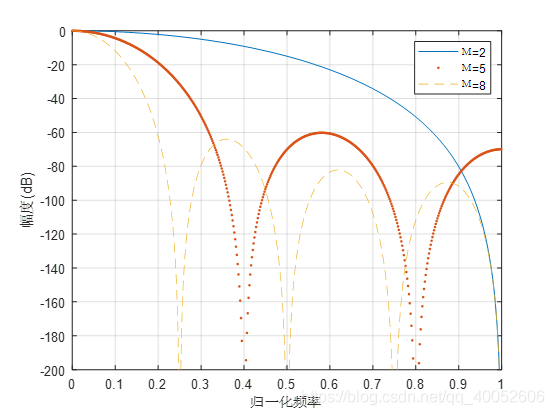
从上图可知第一旁瓣衰减67.3dB,但多级CIC主瓣内电平值下降也是较快,这就说明了在相同的通带内滤波器的通带衰减也明显增加。针对通带内衰减问题,可以通过在自定义的通带内来通过比较多级级联的衰减来说明问题,这里设置归一化通带为0.2,级联数目为D,进行MATLAB仿真,代码如下:
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s5=filter(b,1,s4); %求取滤波器冲激响应
Spec1=20*log10(abs(fft(s1)));%求取滤波器频谱特性
Spec1=Spec1-max(Spec1);
Spec2=20*log10(abs(fft(s2)));%求取滤波器频谱特性
Spec2=Spec2-max(Spec2);
Spec3=20*log10(abs(fft(s3)));%求取滤波器频谱特性
Spec3=Spec3-max(Spec3);
Spec4=20*log10(abs(fft(s4)));%求取滤波器频谱特性
Spec4=Spec4-max(Spec4);
Spec5=20*log10(abs(fft(s5)));%求取滤波器频谱特性
Spec5=Spec5-max(Spec5);
f=0:length(Spec1)-1;
f=2*f/(length(Spec1)-1); %对频率轴进行归一化处理
plot(f,Spec1,’-’,f,Spec2,’。’,f,Spec3,’–’,f,Spec5,’-。’);axis([0 0.2 -25 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘D=1’,‘D=2’,‘D=3’,‘D=5’);
grid;
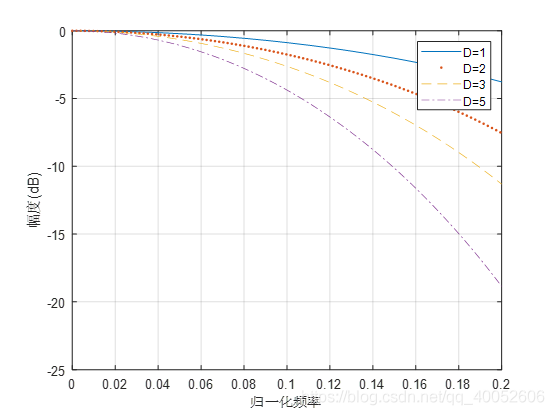
从图中可以看出随着级联数码的增加通带内衰减越大。
因此在实际应用中要根据输入信号和输出信号的特性来进行使用和级联。需要注意的是CIC抽取并不会造成信号幅度的损失,但经过FFT后频谱幅度与所取的点数成正比,因此抽取后信号的幅度将变为原始信号频谱幅度发1/M(M是抽取系数)。抽取滤波器其实就是低通滤波器,因此低通滤波器的特性CIC抽取滤波器依然具有。
CIC抽取滤波器MATLAB仿真和FPGA实现(1)
设计理想滤波器目标:1、滤波器在有效频段内纹波满足设计要求。2、抽取或内插处理后在有效频段内不产生混叠。3、滤波器实现简单,需要资源较少。这个文章主要讲CIC理论基础,下个文章讲FPGA实现。
级联积分梳状滤波器又称CIC。这是多速率信号处理中一种结构简单的滤波器,只需要加法器和寄存器即可实现,可以灵活的设置抽取因子和插值因子,并且CIC是一种基于零点和极点相消的FIR滤波器。
CIC是由积分器和梳状滤波器组成。积分器可表示为(太多公式了只能截图发出来)

根据上面的分析可以知道积分器对直流有着无限的的增益,在应用时这是一个不稳定的系统。
梳状滤波器可表示为

单级CIC在不同延时长度时冲击响应的频谱特性MATLAB代码如下:
M=2; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s=filter(b,1,delta); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec8=Spec-max(Spec);
%plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
%xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
%legend(‘M=2’,‘M=5’,‘M=7’,‘M=8’);
%grid;
plot(f,Spec2,’-’,f,Spec5,’。’,f,Spec8,’–’);axis([0 1 -50 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘M=2’,‘M=5’,‘M=8’);
grid;
幅频响应如下图:


理论计算与上图仿真结果相对应。
然而在实际应用中第一级抑制比太低,可以通过级联CIC的方式得到想要的抑制比。在RM一定的情况下由于级联后传递函数是乘机的关系,因此抑制比是累加的关系,如四级CIC级联后第一旁瓣抑制比在53.84dB。但是增加滤波器级联数目虽然可以解决旁瓣电平衰减减小问题,但是会带来通带衰减较大的问题,并且在实现时会消耗更多的资源。下面是5级CIC级联不同RM的MATLAB代码和频谱特性图
M=2; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec2=Spec-max(Spec);
f=0:length(Spec)-1;
f=2*f/(length(Spec)-1); %对频率轴进行归一化处理
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec5=Spec-max(Spec);
M=7; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec7=Spec-max(Spec);
M=8; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s=filter(b,1,s4); %求取滤波器冲激响应
Spec=20*log10(abs(fft(s)));%求取滤波器频谱特性
Spec8=Spec-max(Spec);
%plot(f,Spec2,f,Spec5,f,Spec7,f,Spec8);axis([0 1 -50 0]);grid;
%xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
%legend(‘M=2’,‘M=5’,‘M=7’,‘M=8’);
%grid;
plot(f,Spec2,’-’,f,Spec5,’。’,f,Spec8,’–’);axis([0
1 -200 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘M=2’,‘M=5’,‘M=8’);
grid;

从上图可知第一旁瓣衰减67.3dB,但多级CIC主瓣内电平值下降也是较快,这就说明了在相同的通带内滤波器的通带衰减也明显增加。针对通带内衰减问题,可以通过在自定义的通带内来通过比较多级级联的衰减来说明问题,这里设置归一化通带为0.2,级联数目为D,进行MATLAB仿真,代码如下:
M=5; %滤波器长度
b=ones(1,M);
delta=[1,zeros(1,1023)];
s1=filter(b,1,delta); %求取滤波器冲激响应
s2=filter(b,1,s1); %求取滤波器冲激响应
s3=filter(b,1,s2); %求取滤波器冲激响应
s4=filter(b,1,s3); %求取滤波器冲激响应
s5=filter(b,1,s4); %求取滤波器冲激响应
Spec1=20*log10(abs(fft(s1)));%求取滤波器频谱特性
Spec1=Spec1-max(Spec1);
Spec2=20*log10(abs(fft(s2)));%求取滤波器频谱特性
Spec2=Spec2-max(Spec2);
Spec3=20*log10(abs(fft(s3)));%求取滤波器频谱特性
Spec3=Spec3-max(Spec3);
Spec4=20*log10(abs(fft(s4)));%求取滤波器频谱特性
Spec4=Spec4-max(Spec4);
Spec5=20*log10(abs(fft(s5)));%求取滤波器频谱特性
Spec5=Spec5-max(Spec5);
f=0:length(Spec1)-1;
f=2*f/(length(Spec1)-1); %对频率轴进行归一化处理
plot(f,Spec1,’-’,f,Spec2,’。’,f,Spec3,’–’,f,Spec5,’-。’);axis([0 0.2 -25 0]);
xlabel(‘归一化频率’);ylabel(‘幅度(dB)’);
legend(‘D=1’,‘D=2’,‘D=3’,‘D=5’);
grid;

从图中可以看出随着级联数码的增加通带内衰减越大。
因此在实际应用中要根据输入信号和输出信号的特性来进行使用和级联。需要注意的是CIC抽取并不会造成信号幅度的损失,但经过FFT后频谱幅度与所取的点数成正比,因此抽取后信号的幅度将变为原始信号频谱幅度发1/M(M是抽取系数)。抽取滤波器其实就是低通滤波器,因此低通滤波器的特性CIC抽取滤波器依然具有。

 举报
举报








 举报
举报

