一、电机离散域模型
本文讨论的仅针对dq轴相等的电机,如表贴式永磁同步电机。
复矢量模型可在永磁同步电机控制之反馈解耦及复矢量解耦一文中查看。
下面的推导过程直接使用我用word写的截图:




二、离散域中解耦算法的分析
连续时域中针对两个常用解耦算法(反馈解耦与复矢量解耦)的讲解在永磁同步电机控制之反馈解耦及复矢量解耦一文中查看。
下面是离散时域中与连续时域中的对比。
1.反馈解耦
如下图(a)所示,在连续时域中以零极点对消原理为基础设计的反馈解耦PI调节器解耦性能较好,主导极点与零点相消,且不受转速增大影响,说明不考虑设计调节器所用的电机参数与实际值之间误差的影响,该系统实现了完全解耦,且该系统为稳定系统。但将反馈解耦PI调节器离散化再以数字方式实现后,性能受到制约,如下图(b)所示,同样参数的情况下,离散时域中反馈解耦PI调节器靠近单位圆边界的极点未与零点相消,并随着转速增大逐渐向单位圆边界逼近,反映出离散时域中,反馈解耦PI调节器的控制性能较差,未能做到完全解耦,且随着转速增大,系统稳定性下降。
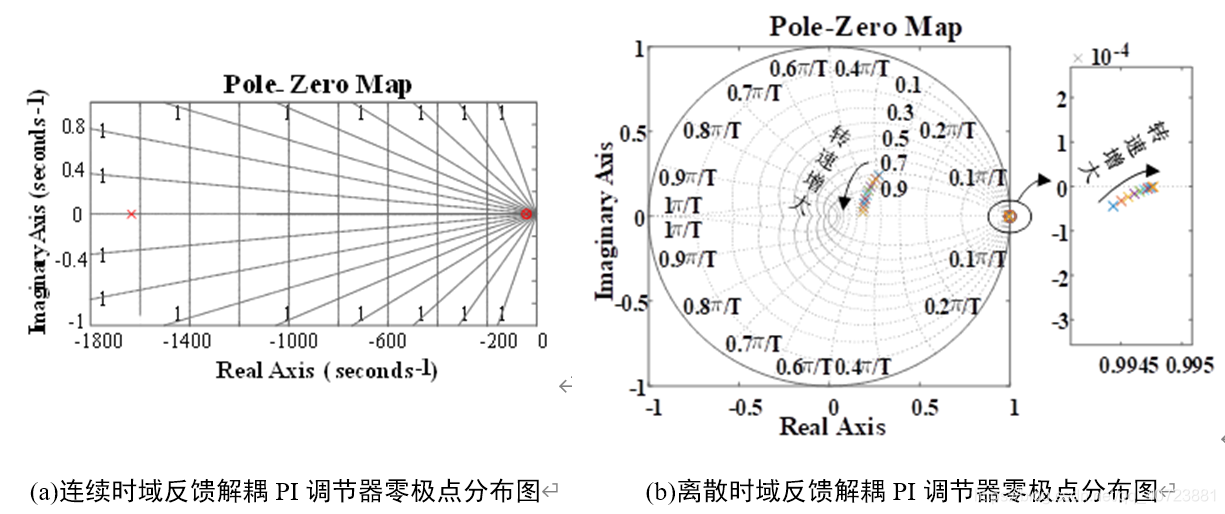
2.复矢量解耦
如下图(a)所示,在连续时域中以零极点对消原理为基础设计的复矢量PI调节器解耦性能较好,主导极点与零点相消,且不受转速增大的影响,说明在连续时域中,不考虑设计调节器所用的电机参数与实际值之间误差的影响,复矢量PI调节器可做到完全解耦,但将其离散化以数字方式实现后,性能受到制约,如下图(b)所示,离散时域中同参数复矢量解耦PI调节器存在单位圆之外的极点,且单位圆中的极点未与零点相消,并随着转速增大向单位圆边界逼近,反映出离散时域中,复矢量解耦PI调节器的控制性能较差,未能做到完全解耦,且系统是不稳定系统。
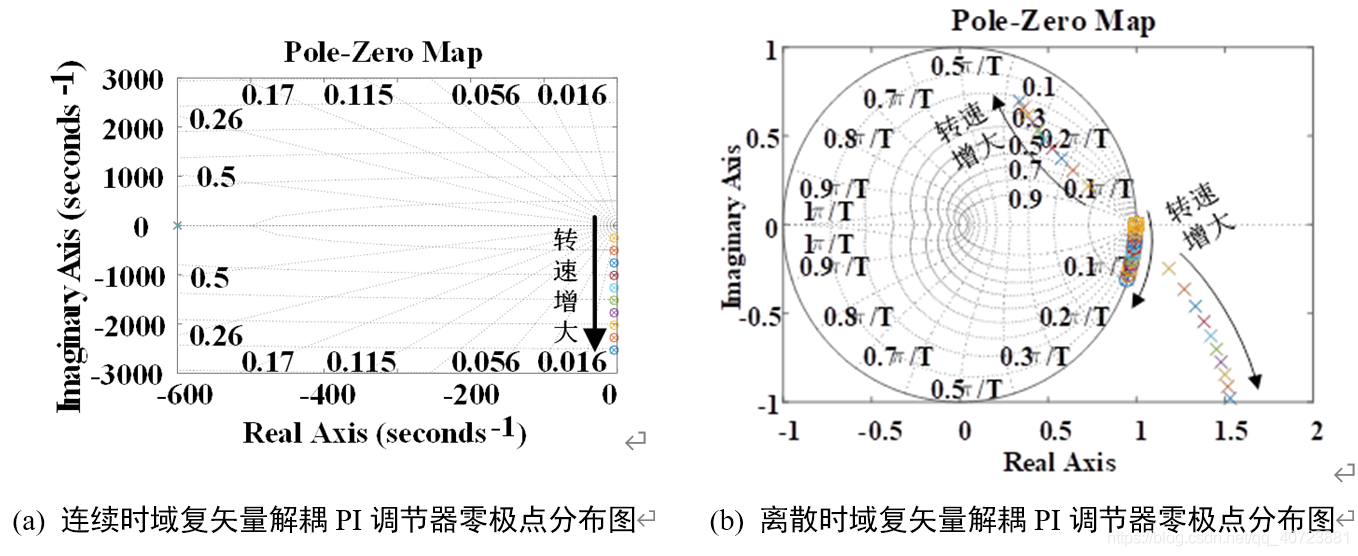
三、离散域中设计电流调节器
1.理论设计

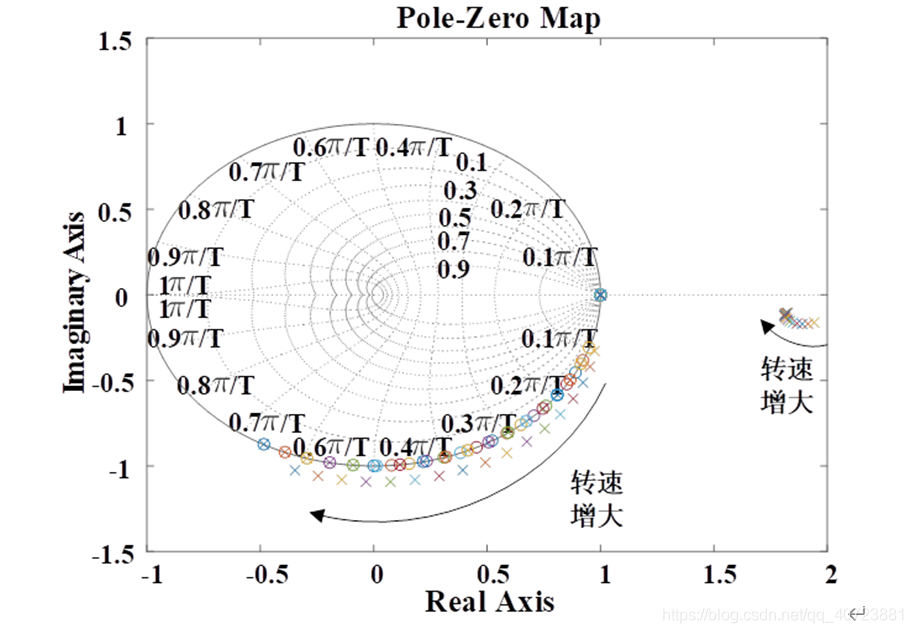
进而可绘制电机控制系统的零极点分布图。如下图所示,随着转速增大,系统变化的极点一直被零点抵消,且单位圆外没有极点,反映该控制系统是稳定的。其次,圆内极点没有向单位圆边界靠近的趋势,反映该系统没有不稳定的趋势。这两点表明相较在连续时域设计再离散化的复矢量PI调节器,直接在离散时域设计的复矢量PI调节器性能更优。
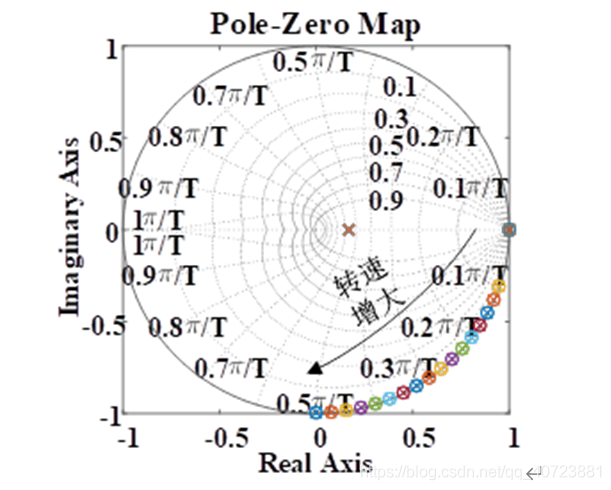
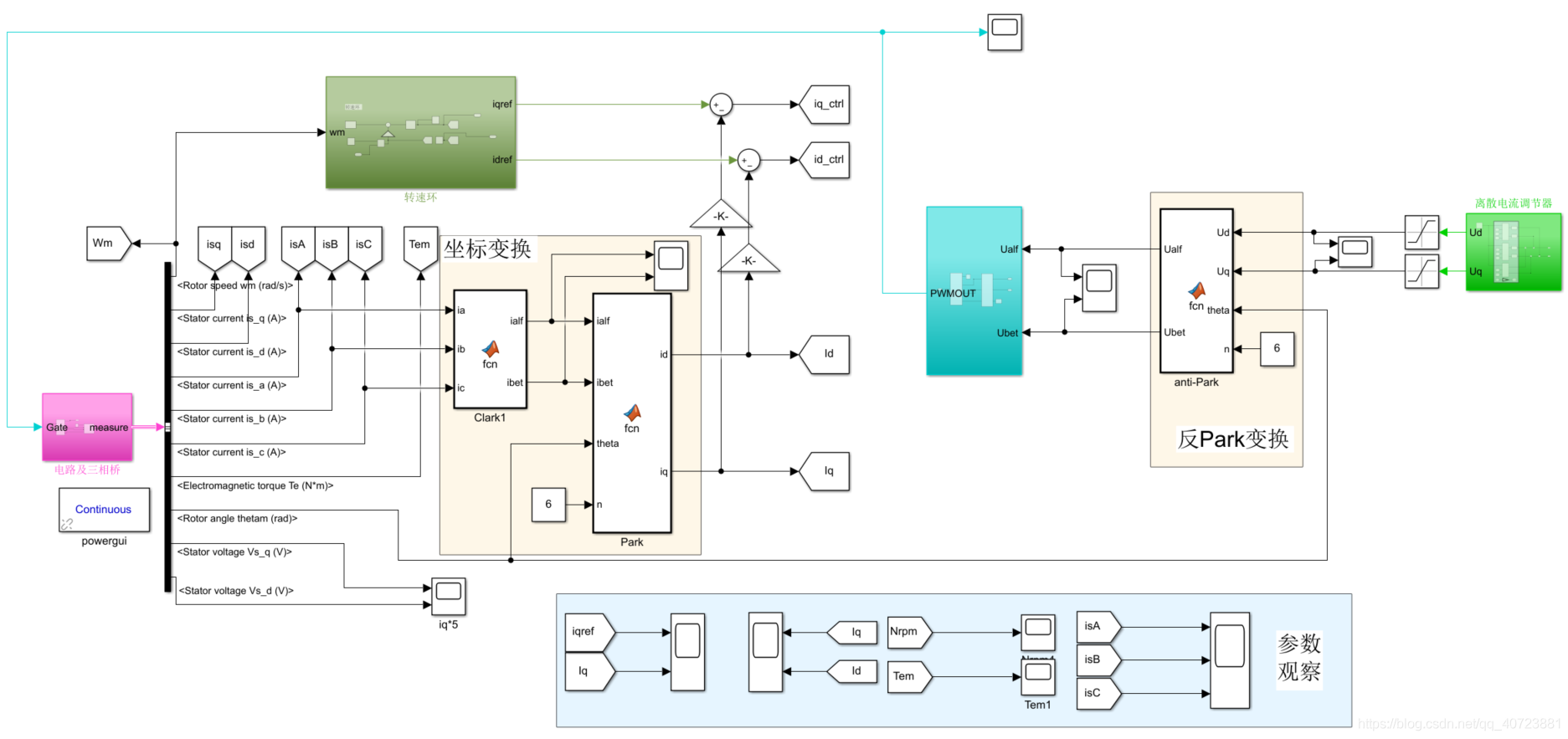
2.实际实现
使用数学表达式不太容易直观表现实际是如何实现的,首先,式(3-2)中有虚部部分,此虚部部分直接欧拉公式展开,并代入dq轴误差计算dq轴电压给定:
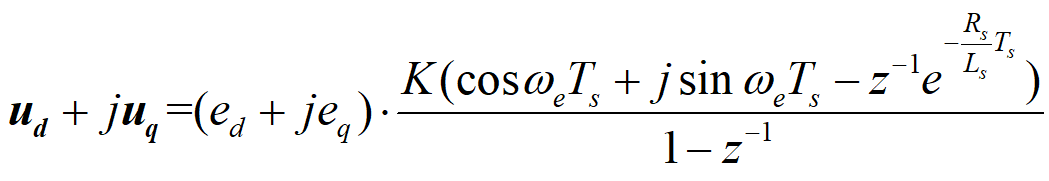
接着等式右边的实部对应等式左边的实部,等式右边的虚部对应等式左边的虚部,可以得到:
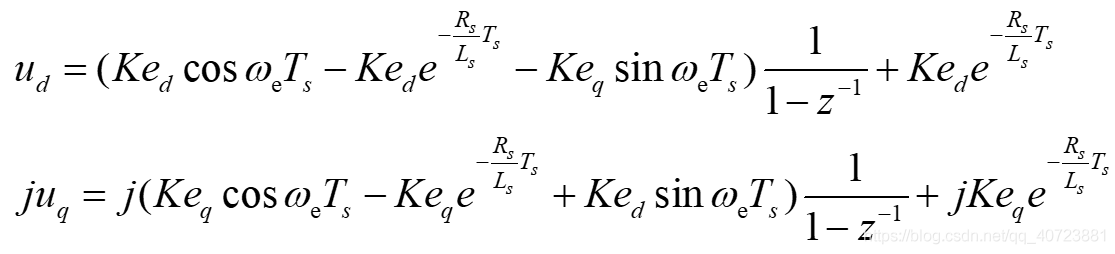
则绘制其控制框图用以指导电流调节器的实现:
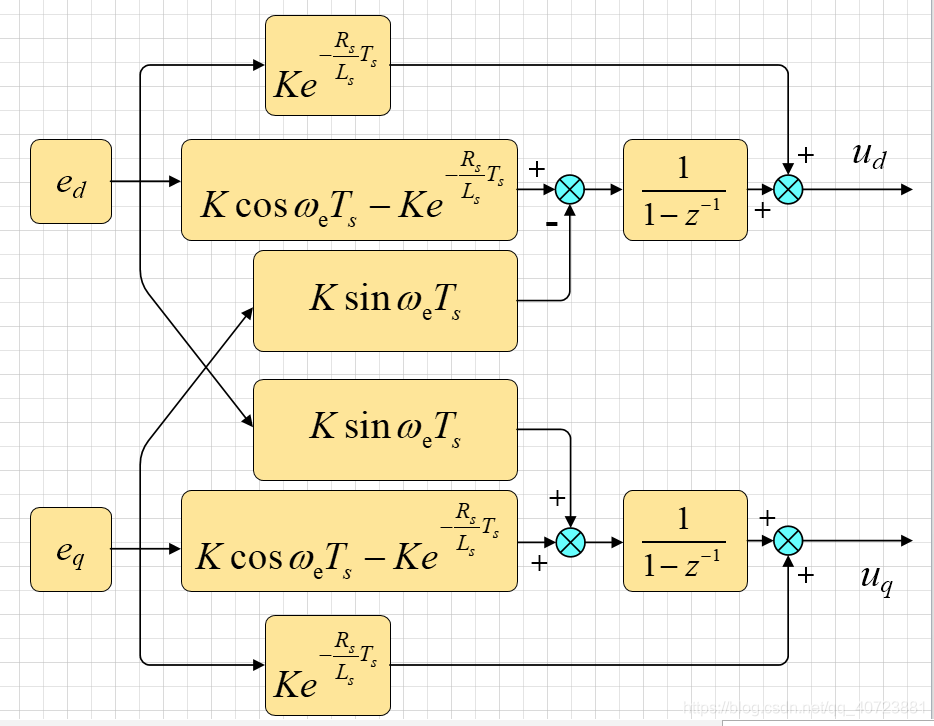
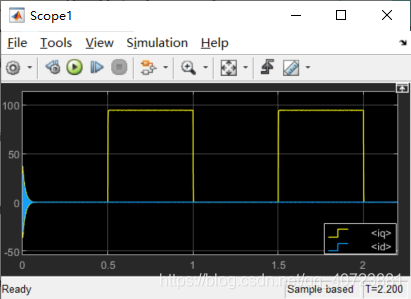
其中ed,eq分别为d轴电流误差与q轴电流误差,ud,uq即为输给反park变换的dq轴电压给定。
结语
若要进一步考虑内嵌式永磁同步电机采用Ls =(Ld +Lq)/2替代dq轴电感Ld 、Lq进行建模对控制系统的影响。对于内嵌式永磁同步电机,其数学模型如(2-20)所示,使用如式(3- 2)所示的电流调节器,绘制其零极点分布图,如下图所示,单位圆外面存在极点,表明系统是不稳定系统,且靠近单位圆边界的极点不再被零点抵消,虽然零点的运动轨迹依然与极点相近,但随着转速升高,零点与极点间的差距变大,表明随着转速升高,系统更加不稳定。故在dq轴电感有较大不平衡、载波比较低时,上述调节器也逐渐变得不再适用,需要有针对性的设计新的电流调节器。
一、电机离散域模型
本文讨论的仅针对dq轴相等的电机,如表贴式永磁同步电机。
复矢量模型可在永磁同步电机控制之反馈解耦及复矢量解耦一文中查看。
下面的推导过程直接使用我用word写的截图:




二、离散域中解耦算法的分析
连续时域中针对两个常用解耦算法(反馈解耦与复矢量解耦)的讲解在永磁同步电机控制之反馈解耦及复矢量解耦一文中查看。
下面是离散时域中与连续时域中的对比。
1.反馈解耦
如下图(a)所示,在连续时域中以零极点对消原理为基础设计的反馈解耦PI调节器解耦性能较好,主导极点与零点相消,且不受转速增大影响,说明不考虑设计调节器所用的电机参数与实际值之间误差的影响,该系统实现了完全解耦,且该系统为稳定系统。但将反馈解耦PI调节器离散化再以数字方式实现后,性能受到制约,如下图(b)所示,同样参数的情况下,离散时域中反馈解耦PI调节器靠近单位圆边界的极点未与零点相消,并随着转速增大逐渐向单位圆边界逼近,反映出离散时域中,反馈解耦PI调节器的控制性能较差,未能做到完全解耦,且随着转速增大,系统稳定性下降。

2.复矢量解耦
如下图(a)所示,在连续时域中以零极点对消原理为基础设计的复矢量PI调节器解耦性能较好,主导极点与零点相消,且不受转速增大的影响,说明在连续时域中,不考虑设计调节器所用的电机参数与实际值之间误差的影响,复矢量PI调节器可做到完全解耦,但将其离散化以数字方式实现后,性能受到制约,如下图(b)所示,离散时域中同参数复矢量解耦PI调节器存在单位圆之外的极点,且单位圆中的极点未与零点相消,并随着转速增大向单位圆边界逼近,反映出离散时域中,复矢量解耦PI调节器的控制性能较差,未能做到完全解耦,且系统是不稳定系统。

三、离散域中设计电流调节器
1.理论设计

进而可绘制电机控制系统的零极点分布图。如下图所示,随着转速增大,系统变化的极点一直被零点抵消,且单位圆外没有极点,反映该控制系统是稳定的。其次,圆内极点没有向单位圆边界靠近的趋势,反映该系统没有不稳定的趋势。这两点表明相较在连续时域设计再离散化的复矢量PI调节器,直接在离散时域设计的复矢量PI调节器性能更优。

2.实际实现
使用数学表达式不太容易直观表现实际是如何实现的,首先,式(3-2)中有虚部部分,此虚部部分直接欧拉公式展开,并代入dq轴误差计算dq轴电压给定:
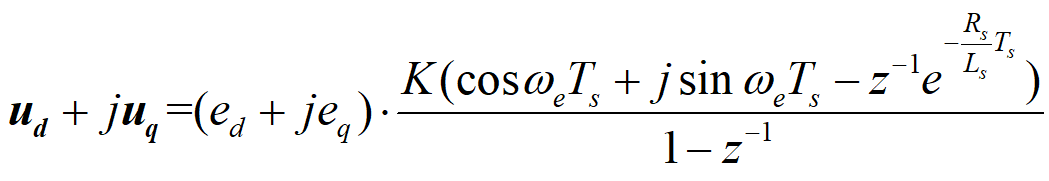
接着等式右边的实部对应等式左边的实部,等式右边的虚部对应等式左边的虚部,可以得到:
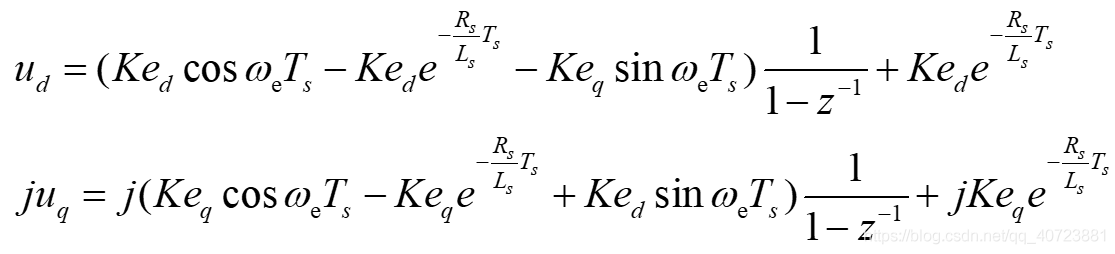
则绘制其控制框图用以指导电流调节器的实现:

其中ed,eq分别为d轴电流误差与q轴电流误差,ud,uq即为输给反park变换的dq轴电压给定。
结语
若要进一步考虑内嵌式永磁同步电机采用Ls =(Ld +Lq)/2替代dq轴电感Ld 、Lq进行建模对控制系统的影响。对于内嵌式永磁同步电机,其数学模型如(2-20)所示,使用如式(3- 2)所示的电流调节器,绘制其零极点分布图,如下图所示,单位圆外面存在极点,表明系统是不稳定系统,且靠近单位圆边界的极点不再被零点抵消,虽然零点的运动轨迹依然与极点相近,但随着转速升高,零点与极点间的差距变大,表明随着转速升高,系统更加不稳定。故在dq轴电感有较大不平衡、载波比较低时,上述调节器也逐渐变得不再适用,需要有针对性的设计新的电流调节器。




 举报
举报








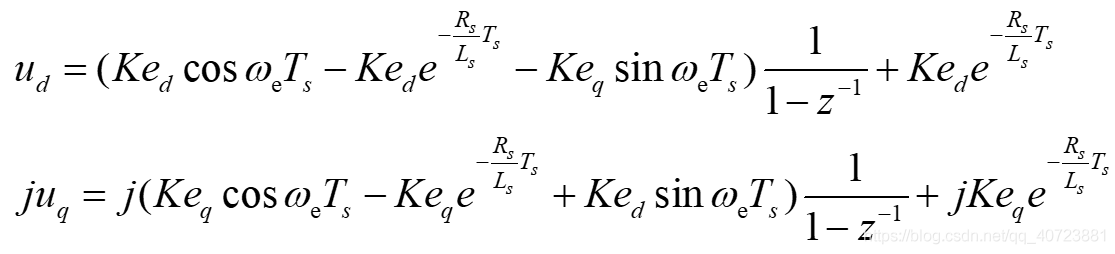





 举报
举报

