1 原理分析
SVPWM算法实际上是对应于交流电机中的三相电压源逆变器功率器件的一种特殊的开关触发顺序和脉宽大小的组合,这种开关触发顺序和组合将在定子线圈中产生三相互差120电角度、失真较小的正弦波电流波形,也就使电机获得圆形磁链轨迹轨迹。
我们可以通过互差120度,大小随着时间按正弦规律变化的3个分矢量来合成一个大小不变旋转的总矢量。于是只需要控制PWM的占空比按等效正弦:

由于逆变器有6个MOS控制,所以通过上下桥臂不同的开关组合可以定义开关函数Sx(x=a、b、c), 1:上桥臂导通、0:桥臂打开(上下桥臂为互补PWM)。(Sa、Sb、Sc)的全部可能组合共有八个,包括 6个非零矢量Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量 U0(000)、U7(111)。以U4(100)为例,此时等效电路为:

此时相电压可以表示为:
Ua = 2/3 Udc
Ub = -1/3 Udc
Ua = -1/3 Udc
那么最终可以计算出一个合成矢量的关系式:
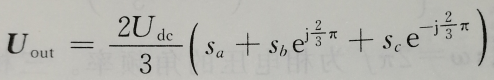
通过将8中开关状带入公式可以得到一个开关组合和电压的关系,将这8钟组合的基本空间矢量映射到平面上后,可以得到电压空间矢量图。他们将平面分成6个区,称之为扇区。
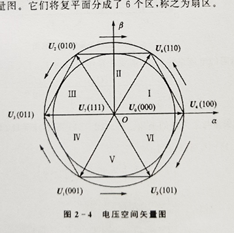
2 算法合成原理
SVPWM算法的理论基础是平均等效原理,即在一个开关周期Ts内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。如下图,在某个时刻,电压空间矢量Uout旋转到某个区域内,可以由组成该区域的两个相邻的非零矢量和零矢量在时间上的不同组合得到。以扇区I为例,可得下式:
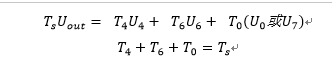


此时就得到了U4、U6、U7、U0对应的时间。因此就可以利用 U4、U6、U7 及 U0 的顺序和时间长短的搭配来表示出Uref了
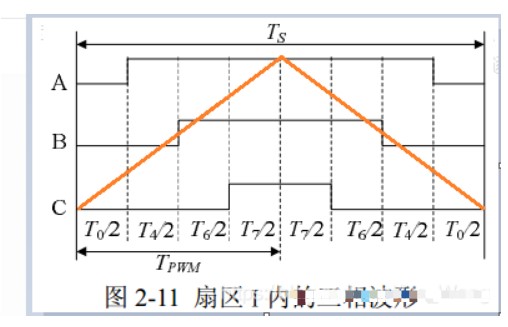
那么按照不同的开关顺序,就可以得到对称的输出波形,开关顺序如下:
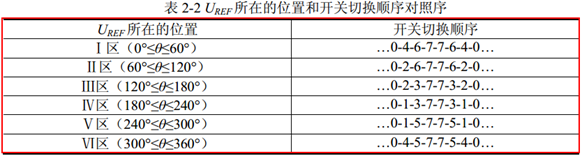
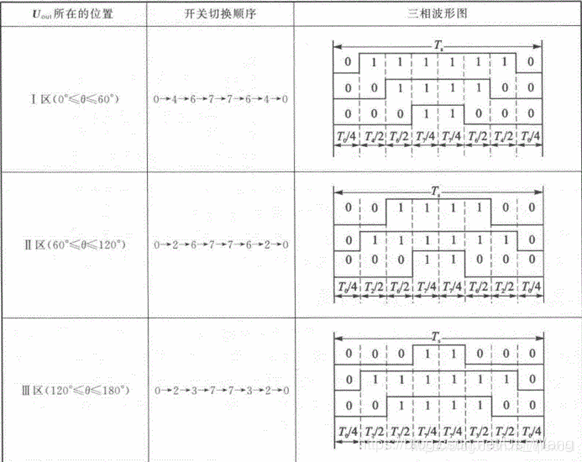

无论在仿真中还是实际单片机定时器,其产生的三相波调制波形在一个载波周期(三角波)Ts内。通过电角度的循环变化,各项电压的三相波形与表2-2开关顺序对应。每个载波周期Ts就会合成一个新的矢量,随着电角度的逐步增大,Uref 将依序进入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ区。
3 算法实现
3.1 输入输出参数
无论是基于控制板还是Simulink仿真,算法的实现都要有明确的逻辑。首先需要知道SVPWM模块或函数的输入输出参数。

由FOC控制流程图可知SVPWM输入为Valpha跟Vbeta,输出为三相电压。在simulink仿真中,我们需要输入Valpha跟Vbet,输出UVW对应的有效电平时间即可。在MCU中,以ST32f103为例,需要输入Valpha跟Vbet,输出UVW对应的定时器比较值即可。
3.2 扇区确定
用Valpha跟Vbeta表示参考电压Uout在alpha、beta轴上的分量,那么定义Uref1、Uref2、Uref3三个变量,令
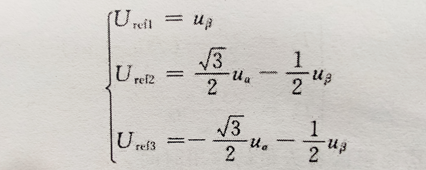
扇区计算可以看作比较大小的过程,判断β是否大于0,确定扇区在V3,V4矢量连成的直线的上方还是下方,sqrt(3)/2α 与β/2比较大小,确定扇区在V1,V6所连成直线的左边还是右边,-sqrt(3)/2α 与β/2比较大小,确定扇区在V2,V5连成直线的左边还是右边。
再定义,若Uref1 》 0 ,则 A=1,否则 A=0;
若Uref2 》 0 ,则B=1,否则 B=0;
若Uref3 》 0 ,则 C=1,否则 C=0。
因此可以由A、B、C的组合判断当前Uout所在的扇区, N=4C+2B+A,则可以通过下表计算参考电压矢量Uout所在的扇区。

3.3 输出时间确定
根据电压矢量在Valpha跟Vbeta的分量,可以计算出Uout在各个扇区中各矢量的作用时间,如下表所示,其中两个非零矢量作用时间的比例系数为K = √3Ts/Udc 。

当两个零电压矢量作用时间为0时,一个Ts周期内,非零矢量的作用时间最长。此时合成的空间电压矢量幅值最大,最大不会超过正六边形边界。若超过边界,将会发生过调制,逆变器输出电压波形将发生失真,因此需要将输出电压矢量在正六边形的内切圆里。,其幅值为1/√3 Udc。
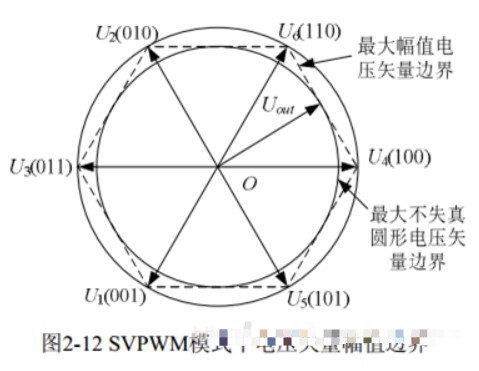
因此需要保证非零矢量时间和小于周期Ts。所以关系为:

至此,SVPWM的算法流程为
① 根据Ualpah和Ubeta计算扇区
② 计算非零矢量以及零矢量作用时间
4 Simulink仿真
在确定原理之后,我们开始进行simulin搭建。
4.1 创建Ud和Uq的输入。
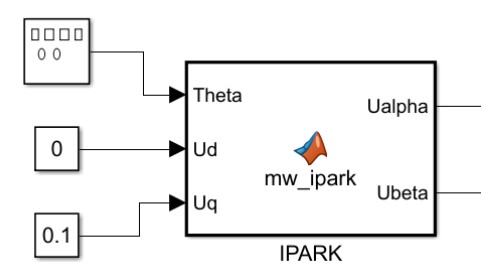
这是可能会有一个疑问,为什么要Ud = 0,Uq为一个定值呢?
因为根据Ud、Uq的电压公式,Ud = 0,及Id = 0;在Uq的范围内,Iq随电气角速度的变大而减小。此时Ualpha与Ubeta 的波形如下:

然后使用MATLAB Function模块设计SVPWM的代码,这样简单一些,也可以直接将代码稍微修改带电机控制算法中。
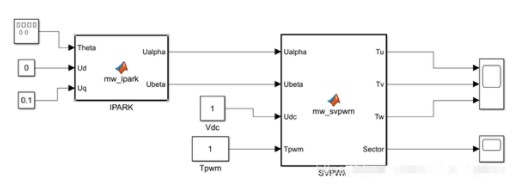
4.2 根据Ualpha跟Ubeta确定电压矢量扇区
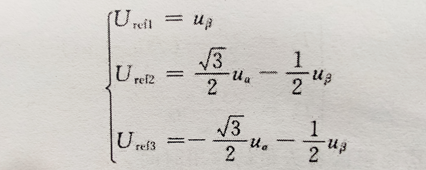

%
% 参考电压矢量的扇区判断
% 若Uref1 》 0,则A = 1,否则A = 0;
% 若Uref2 》 0,则B = 1,否则B = 0;
% 若Uref3 》 0,则C = 1,否则C = 0;
% Sector = 4C + 2B + A
% N与扇区的对应位:
% Sector : 3 1 5 4 6 2
% 扇区号 : I II III IV V VI
%
Uref1 = Ubeta;
Uref2 = (sqrt(3) * Ualpha - Ubeta) / 2;
Uref3 = (-sqrt(3) * Ualpha - Ubeta) / 2;
if Uref1 》 0
Sector = 1;
end
if Uref2 》 0
Sector = Sector + 2;
end
if Uref3 》 0
Sector = Sector + 4;
end
4.3 计算各扇区输出时间

4.4 计算各扇区输出时间
X = sqrt(3) * Ubeta * Tpwm / Udc ;
Y = Tpwm / Udc * ( 3/2 * Ualpha + sqrt(3)/2 * Ubeta);
Z = Tpwm / Udc * (-3/2 * Ualpha + sqrt(3)/2 * Ubeta);
switch (Sector)
case 1
T1 = Z; T2 = Y;
case 2
T1 = Y; T2 = -X;
case 3
T1 = -Z; T2 = X;
case 4
T1 = -X; T2 = Z;
case 5
T1 = X; T2 = -Y;
otherwise
T1 = -Y; T2 = -Z;
end
4.5 过调整处理
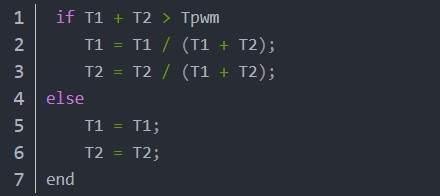
这个时候要注意了,在simulink中调制周期Ts是由三角波生成的,那么每个输出时间应以Ts/2为参考,若使用锯齿波为周期,那么计算的三相电压时间就不用除2。为了兼容各个MCU对PWM的设计,这里选择使用锯齿波方式,三相时间不除2,如下图:

三角波:
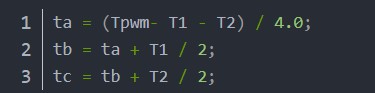
锯齿波:
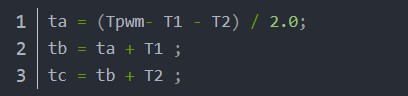
4.6 三相电压有效值时间输出
switch Sector
case 0 % (Ualpha,Ubeta) = (0,0)
Tu = 0.5;
Tv = 0.5;
Tw = 0.5;
case 1 % II 扇区 0-》2-》6-》7-》7-》6-》2-》0
Tu = tb;
Tv = ta;
Tw = tc;
case 2 % VI 扇区 0-》4-》5-》7-》7-》5-》4-》0
Tu = ta;
Tv = tc;
Tw = tb;
case 3 % I 扇区 0-》4-》6-》7-》7-》6-》4-》0
Tu = ta;
Tv = tb;
Tw = tc;
case 4 % IV 扇区 0-》1-》3-》7-》7-》3-》1-》0
Tu = tc;
Tv = tb;
Tw = ta;
case 5 % III扇区 0-》2-》3-》7-》7-》3-》2-》0
Tu = tc;
Tv = ta;
Tw = tb;
case 6 % V 扇区 0-》1-》5-》7-》7-》5-》1-》0
Tu = tb;
Tv = tc;
Tw = ta;
end
5 波形分析
当设置Uq = 0.1,Ts=1时,Ualpha与Ubeta幅值为0.1,最终算出的SVPWM的作用时间应已0.5为中心,上下波动,由于选择的是内切圆。这是需要明确一个概念(自己意淫的,但给自己说通了),相电压与线电压。
由于α-β轴与d-q轴都可以理解为由“相”角度变换而来,所以都是“相”的概念,而电源电压作用到的是三相,要形成回路,所以可以理解为“线”的概念,因此Uq输入的值要除以sqrt(3)。这也是电压Q值标幺化时,最大电压为Udc / sqrt(3)。
当Uq设置为1/sqrt(3)时,SVPWM输出为:
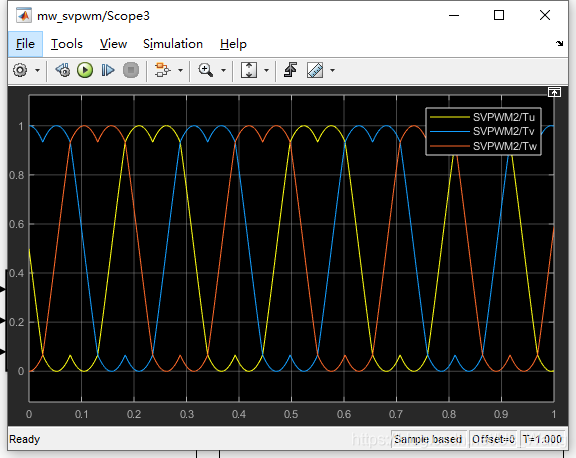
可以看到三相调制波均为漂亮的马鞍波,波峰接近1,波谷接近0,已经接近逆变器不失真输出的极限。
扇区变化如下:

基于控制板SVPWM设计
使用ST32F103C8T6设计SVPWM输出,整个算法层使用Q24定标的Q值格式。如下图Uq的变化与SVPWM输出波形。可以看到Uq为0.1时,SVPWM与仿真的基本一样。

1 原理分析
SVPWM算法实际上是对应于交流电机中的三相电压源逆变器功率器件的一种特殊的开关触发顺序和脉宽大小的组合,这种开关触发顺序和组合将在定子线圈中产生三相互差120电角度、失真较小的正弦波电流波形,也就使电机获得圆形磁链轨迹轨迹。
我们可以通过互差120度,大小随着时间按正弦规律变化的3个分矢量来合成一个大小不变旋转的总矢量。于是只需要控制PWM的占空比按等效正弦:

由于逆变器有6个MOS控制,所以通过上下桥臂不同的开关组合可以定义开关函数Sx(x=a、b、c), 1:上桥臂导通、0:桥臂打开(上下桥臂为互补PWM)。(Sa、Sb、Sc)的全部可能组合共有八个,包括 6个非零矢量Ul(001)、U2(010)、U3(011)、U4(100)、U5(101)、U6(110)、和两个零矢量 U0(000)、U7(111)。以U4(100)为例,此时等效电路为:

此时相电压可以表示为:
Ua = 2/3 Udc
Ub = -1/3 Udc
Ua = -1/3 Udc
那么最终可以计算出一个合成矢量的关系式:
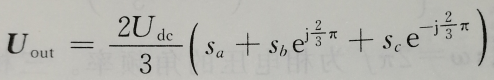
通过将8中开关状带入公式可以得到一个开关组合和电压的关系,将这8钟组合的基本空间矢量映射到平面上后,可以得到电压空间矢量图。他们将平面分成6个区,称之为扇区。

2 算法合成原理
SVPWM算法的理论基础是平均等效原理,即在一个开关周期Ts内通过对基本电压矢量加以组合,使其平均值与给定电压矢量相等。如下图,在某个时刻,电压空间矢量Uout旋转到某个区域内,可以由组成该区域的两个相邻的非零矢量和零矢量在时间上的不同组合得到。以扇区I为例,可得下式:
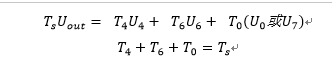


此时就得到了U4、U6、U7、U0对应的时间。因此就可以利用 U4、U6、U7 及 U0 的顺序和时间长短的搭配来表示出Uref了

那么按照不同的开关顺序,就可以得到对称的输出波形,开关顺序如下:



无论在仿真中还是实际单片机定时器,其产生的三相波调制波形在一个载波周期(三角波)Ts内。通过电角度的循环变化,各项电压的三相波形与表2-2开关顺序对应。每个载波周期Ts就会合成一个新的矢量,随着电角度的逐步增大,Uref 将依序进入第Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ区。
3 算法实现
3.1 输入输出参数
无论是基于控制板还是Simulink仿真,算法的实现都要有明确的逻辑。首先需要知道SVPWM模块或函数的输入输出参数。

由FOC控制流程图可知SVPWM输入为Valpha跟Vbeta,输出为三相电压。在simulink仿真中,我们需要输入Valpha跟Vbet,输出UVW对应的有效电平时间即可。在MCU中,以ST32f103为例,需要输入Valpha跟Vbet,输出UVW对应的定时器比较值即可。
3.2 扇区确定
用Valpha跟Vbeta表示参考电压Uout在alpha、beta轴上的分量,那么定义Uref1、Uref2、Uref3三个变量,令
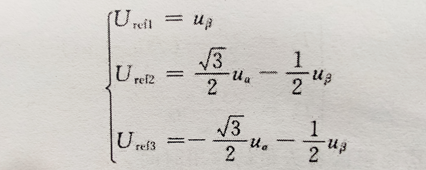
扇区计算可以看作比较大小的过程,判断β是否大于0,确定扇区在V3,V4矢量连成的直线的上方还是下方,sqrt(3)/2α 与β/2比较大小,确定扇区在V1,V6所连成直线的左边还是右边,-sqrt(3)/2α 与β/2比较大小,确定扇区在V2,V5连成直线的左边还是右边。
再定义,若Uref1 》 0 ,则 A=1,否则 A=0;
若Uref2 》 0 ,则B=1,否则 B=0;
若Uref3 》 0 ,则 C=1,否则 C=0。
因此可以由A、B、C的组合判断当前Uout所在的扇区, N=4C+2B+A,则可以通过下表计算参考电压矢量Uout所在的扇区。

3.3 输出时间确定
根据电压矢量在Valpha跟Vbeta的分量,可以计算出Uout在各个扇区中各矢量的作用时间,如下表所示,其中两个非零矢量作用时间的比例系数为K = √3Ts/Udc 。

当两个零电压矢量作用时间为0时,一个Ts周期内,非零矢量的作用时间最长。此时合成的空间电压矢量幅值最大,最大不会超过正六边形边界。若超过边界,将会发生过调制,逆变器输出电压波形将发生失真,因此需要将输出电压矢量在正六边形的内切圆里。,其幅值为1/√3 Udc。

因此需要保证非零矢量时间和小于周期Ts。所以关系为:

至此,SVPWM的算法流程为
① 根据Ualpah和Ubeta计算扇区
② 计算非零矢量以及零矢量作用时间
4 Simulink仿真
在确定原理之后,我们开始进行simulin搭建。
4.1 创建Ud和Uq的输入。

这是可能会有一个疑问,为什么要Ud = 0,Uq为一个定值呢?
因为根据Ud、Uq的电压公式,Ud = 0,及Id = 0;在Uq的范围内,Iq随电气角速度的变大而减小。此时Ualpha与Ubeta 的波形如下:

然后使用MATLAB Function模块设计SVPWM的代码,这样简单一些,也可以直接将代码稍微修改带电机控制算法中。

4.2 根据Ualpha跟Ubeta确定电压矢量扇区
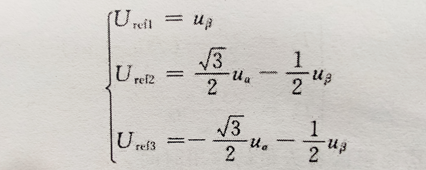

%
% 参考电压矢量的扇区判断
% 若Uref1 》 0,则A = 1,否则A = 0;
% 若Uref2 》 0,则B = 1,否则B = 0;
% 若Uref3 》 0,则C = 1,否则C = 0;
% Sector = 4C + 2B + A
% N与扇区的对应位:
% Sector : 3 1 5 4 6 2
% 扇区号 : I II III IV V VI
%
Uref1 = Ubeta;
Uref2 = (sqrt(3) * Ualpha - Ubeta) / 2;
Uref3 = (-sqrt(3) * Ualpha - Ubeta) / 2;
if Uref1 》 0
Sector = 1;
end
if Uref2 》 0
Sector = Sector + 2;
end
if Uref3 》 0
Sector = Sector + 4;
end
4.3 计算各扇区输出时间

4.4 计算各扇区输出时间
X = sqrt(3) * Ubeta * Tpwm / Udc ;
Y = Tpwm / Udc * ( 3/2 * Ualpha + sqrt(3)/2 * Ubeta);
Z = Tpwm / Udc * (-3/2 * Ualpha + sqrt(3)/2 * Ubeta);
switch (Sector)
case 1
T1 = Z; T2 = Y;
case 2
T1 = Y; T2 = -X;
case 3
T1 = -Z; T2 = X;
case 4
T1 = -X; T2 = Z;
case 5
T1 = X; T2 = -Y;
otherwise
T1 = -Y; T2 = -Z;
end
4.5 过调整处理

这个时候要注意了,在simulink中调制周期Ts是由三角波生成的,那么每个输出时间应以Ts/2为参考,若使用锯齿波为周期,那么计算的三相电压时间就不用除2。为了兼容各个MCU对PWM的设计,这里选择使用锯齿波方式,三相时间不除2,如下图:

三角波:

锯齿波:

4.6 三相电压有效值时间输出
switch Sector
case 0 % (Ualpha,Ubeta) = (0,0)
Tu = 0.5;
Tv = 0.5;
Tw = 0.5;
case 1 % II 扇区 0-》2-》6-》7-》7-》6-》2-》0
Tu = tb;
Tv = ta;
Tw = tc;
case 2 % VI 扇区 0-》4-》5-》7-》7-》5-》4-》0
Tu = ta;
Tv = tc;
Tw = tb;
case 3 % I 扇区 0-》4-》6-》7-》7-》6-》4-》0
Tu = ta;
Tv = tb;
Tw = tc;
case 4 % IV 扇区 0-》1-》3-》7-》7-》3-》1-》0
Tu = tc;
Tv = tb;
Tw = ta;
case 5 % III扇区 0-》2-》3-》7-》7-》3-》2-》0
Tu = tc;
Tv = ta;
Tw = tb;
case 6 % V 扇区 0-》1-》5-》7-》7-》5-》1-》0
Tu = tb;
Tv = tc;
Tw = ta;
end
5 波形分析
当设置Uq = 0.1,Ts=1时,Ualpha与Ubeta幅值为0.1,最终算出的SVPWM的作用时间应已0.5为中心,上下波动,由于选择的是内切圆。这是需要明确一个概念(自己意淫的,但给自己说通了),相电压与线电压。
由于α-β轴与d-q轴都可以理解为由“相”角度变换而来,所以都是“相”的概念,而电源电压作用到的是三相,要形成回路,所以可以理解为“线”的概念,因此Uq输入的值要除以sqrt(3)。这也是电压Q值标幺化时,最大电压为Udc / sqrt(3)。
当Uq设置为1/sqrt(3)时,SVPWM输出为:

可以看到三相调制波均为漂亮的马鞍波,波峰接近1,波谷接近0,已经接近逆变器不失真输出的极限。
扇区变化如下:

基于控制板SVPWM设计
使用ST32F103C8T6设计SVPWM输出,整个算法层使用Q24定标的Q值格式。如下图Uq的变化与SVPWM输出波形。可以看到Uq为0.1时,SVPWM与仿真的基本一样。


 举报
举报











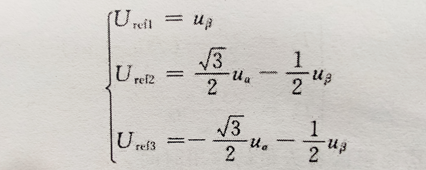






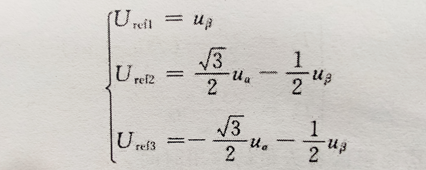









 举报
举报

