本文主要介绍了压缩感知的技术原理,并分析了其在未来基于大规模天线阵列技术的无线通信系统中的应用。
1 技术原理
在数字信号处理中,一般都要经过由模拟信号到数字信号的转换过程,采样和量化是对信号处理的前提条件。
采样定理是1928年由美国电信工程师奈奎斯特首先提出来的,称为奈奎斯特采样定理,该定理指出:要从离散采样信号中无失真的恢复出原始信号,采样率要不低于原始信号带宽的两倍。该理论几乎支配着所有信号的获取、处理、存储、传输等系列过程。
D.Donoho、E.Candes及华裔科学家T.Tao等人对信号稀疏和逼近理论进行了大量深入的研究,于2004年初步提出了一种新的信息获取指导理论:压缩感知理论。该压缩感知理论指出:对可压缩的(稀疏)信号可通过远低于奈奎斯特采样速率进行数据采样后,仍能够精确地恢复出原始信号。
压缩感知突破了奈奎斯特采样定理的限制,使得信息理论进入一个新的研究阶段,其基本思想是:只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解一个最优化问题就可以从这些少量的投影(或称测量值)中以高概率重构出原信号。
在压缩感知理论的框架下,采样率不决定于原始信号的带宽,而取决于重要信息在信号中的结构和内容,测量值并非是信号的本身,而是从高维到低维的投影值,每个测量值都包含了所有样本信号的少量信息,恢复信号所需测量值的数目远少于采样定理要求的数目。
对于一个N*1维信号s,其中s中包含K个非零元素,信号s经过公式(1)变换得到N*1维变量x,再经过公式(2)得到M*1维测量信号y,压缩感知的目的就是通过测量信号y重构出信号s。
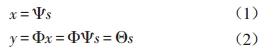
其中,Ψ为N*N维稀疏变换矩阵,Φ为M*N维测量矩阵(也称为投影矩阵或随机采样矩阵),Ψ、Φ的设计会严重影响压缩感知技术的性能,K
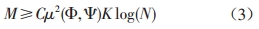
其中,μ2(Φ,Ψ)表示矩阵Ψ、Φ的相关性。
信号重构是压缩感知技术的核心,是一个在获得观测值y的条件下,寻求最稀疏解s的过程,这里需要引入矩阵理论中的范数概念来描述压缩感知理论的信号重构问题。
定义向量Z={z1,z2,…,zN}的P-范数为:
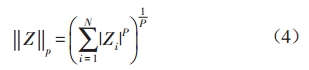
当p=0时得到向量Z的0-范数,表示Z中非零元素的个数。
通常情况下,对于一个非稀疏的信号x在经过稀疏化变换得到s的情况下,压缩感知理论中信号恢复问题,转化为线性约束下的最小0-范数的问题,可以用公式(5)表达:
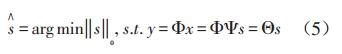
对上述0-范数的优化问题,是一个非凸优化问题,也就是在多项式内无法求解,更不能验证解的有效性,因此需要转换成其他范数,比如1-范数或2-范数,研究证明对于公式(5)最小0-范数问题可以通过求解一个更加简单的1-范数最优化问题得到与0-范数同等的解。因此,压缩感知理论通常用公式(6)描述:
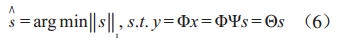
针对公式(6)的求解可以用线性规划算法等最优化理论实现,实际实现时也可以使用其他快速优化算法。
2 应用分析
压缩感知应用特征包括:
(1)观测信号不具有稀疏性,例如OFDM系统频域信道响应或线性阵列响应。
(2)通过对观测信号的基坐标变换,在另外一组基底下,信号变得稀疏,例如频域信道响应通过DFT变换之后,在时域具有稀疏性。
(3)稀疏性(稀疏位置)具有不可知与变化的特性,这是应用压缩感知的必要条件,如果稀疏位置具有可知性或恒定性。
外场测试表明,大部分无线信道在时域上一般都是多径稀疏的,根据压缩感知理论,这种稀疏性意味着可以大幅度地降低用户专有导频开销。
另外,随着基站侧天线数目增加,无线信道在空域上也同样体现出稀疏性,这意味着通过压缩感知技术可以有效减少小区公有导频的开销。
2.1 用户专有导频设计
根据压缩感知理论,再根据公式(6)可知,具有稀疏性的时域无线信道系数可以由在频域中少量分布的导频观测信号通过压缩感知技术恢复出来。
在未来移动通信系统的用户专有导频设计中,基于压缩感知技术,需要考虑的问题有:
(1)导频数目:估计信道的稀疏度K,然后利用公式(3)大概算一下需要的导频符号的数目m。
(2)导频位置:由测量矩阵决定,设计时一定要保证其随机性,可以根据小区标识、帧号、子帧号、资源位置作为随机矩阵生成因子,获取足够稀疏的导频位置,或者在标准化时预定义若干组随机导频位置,调度时根据系统参数确定使用哪一组随机导频位置,这与现有的LTE系统是明显不同的,现有系统中导频是均匀分布的,其间隔主要考虑了相关带宽。
(3)变换矩阵:优先考虑离散傅里叶变换矩阵。
(4)信号重构:接收方按照图1所示的流程,利用少量的频域导频信道值y,恢复时域信道h,其中目标函数最优化可以使用实现复杂度较低的Stomp算法。

图1 压缩感知技术的信号重构流程
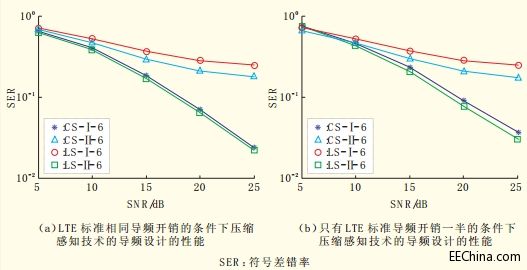
图2 基于压缩感知技术导频设计仿真性能
图2给出了基于压缩感知技术进行用户专有导频设计后与传统的LTE导频相比的性能,图2为在扩展城市环境信道模型(ETU)场景、10MHz、16QAM下的符号差错率(SER)比较,其中LS-Ⅰ-6代表LTE标准导频模式,时域不做基于CP的截断处理,子载波间隔为6的仿真参数设置下的仿真结果;LS-Π-6代表LTE标准导频模式,时域做基于CP的截断处理,子载波间隔为6的仿真参数设置下的仿真结果;CS-Ⅰ-6代表压缩感知导频模式,时域不做基于CP的截断处理,子载波开销与LTE导频开销相同的仿真参数设置下的仿真结果;CS-Π-6代表压缩感知导频模式,时域做基于CP的截断处理,子载波开销与LTE导频开销相同的仿真参数设置下的仿真结果;CS-Ⅰ-12代表压缩感知导频模式,时域不做基于CP的截断处理,子载波开销是LTE导频开销一半的仿真参数设置下的仿真结果;CS-Π-12代表压缩感知导频模式,时域做基于CP的截断处理,子载波开销是LTE导频开销一半的仿真参数设置下的仿真结果。图2(a)给出了在LTE标准相同导频开销的条件下压缩感知技术的导频设计的性能,图2(b)给出了在只有LTE标准导频开销一半的条件下压缩感知技术的导频设计的性能。从仿真结果可以看出,基于压缩感知技术设计的导频可以有效降低系统开销,并提升接收方的解码能力。
2.2 小区公有导频设计
在大规模天线阵列系统中,基站侧天线数目增加,带来了小区公有导频开销的增加,会严重影响未来移动通信系统的性能,因此寻求一种基于低导频密度的信道估计方法变得非常必要。
随着基站侧天线数目增加,信道在空域上是否存在稀疏性是需要首先验证的问题。
图3给出了对基站配置128根天线形成的瞬时信道进行离散傅立叶变换(DFT)后得到的角度域功率谱分布情况,可以看出,变换后得到的变量是具有稀疏性的,因此可以通过压缩感知技术设计未来移动通信系统中的小区公有导频。
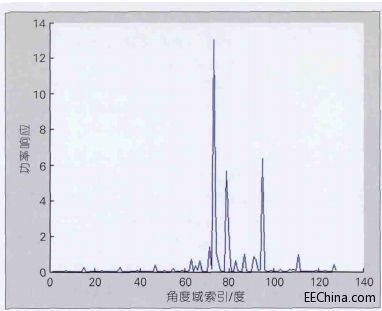
图3 128根天线信道的角度域功率谱分布
小区间公有导频设计导频数目、导频位置、信号重构可参考用户专有导频设计的思路,变换矩阵设计有两种方式:
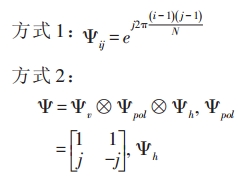
式中Ψ是DFT矩阵。
基于方式1和方式2进行小区间公有导频设计的仿真结果如图4所示。图4为累计分布函数,不考虑干扰/噪声。
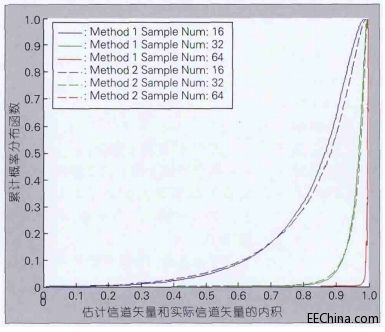
图4 不同变换矩阵空域压缩感知性能分析
可以看出,两种方式都可以比较好地通过压缩感知技术重建空域信道,当随机采样点数目比较多时,两种变换矩阵重建信道时性能差别不大,但是当随机采样点数比较少时,方式2可以更好地重建信道,主要原因在于方式2提供的变换矩阵更好地体现了天线之间的相关性。
3 结束语
通过理论分析及大量仿真,证明了压缩感知技术可以有效地降低系统导频开销,提升系统性能。
后续也可以考虑将压缩感知技术与未来移动通信系统中可能使用的认知无线电技术结合起来用于发现空闲频谱比较多的频段内的空闲资源,有效降低系统硬件实现成本,或者是将压缩感知技术与其他天线降维技术结合起来,提升未来移动通信系统的用户体验。
本文主要介绍了压缩感知的技术原理,并分析了其在未来基于大规模天线阵列技术的无线通信系统中的应用。
1 技术原理
在数字信号处理中,一般都要经过由模拟信号到数字信号的转换过程,采样和量化是对信号处理的前提条件。
采样定理是1928年由美国电信工程师奈奎斯特首先提出来的,称为奈奎斯特采样定理,该定理指出:要从离散采样信号中无失真的恢复出原始信号,采样率要不低于原始信号带宽的两倍。该理论几乎支配着所有信号的获取、处理、存储、传输等系列过程。
D.Donoho、E.Candes及华裔科学家T.Tao等人对信号稀疏和逼近理论进行了大量深入的研究,于2004年初步提出了一种新的信息获取指导理论:压缩感知理论。该压缩感知理论指出:对可压缩的(稀疏)信号可通过远低于奈奎斯特采样速率进行数据采样后,仍能够精确地恢复出原始信号。
压缩感知突破了奈奎斯特采样定理的限制,使得信息理论进入一个新的研究阶段,其基本思想是:只要信号是可压缩的或在某个变换域是稀疏的,那么就可以用一个与变换基不相关的观测矩阵将变换所得高维信号投影到一个低维空间上,然后通过求解一个最优化问题就可以从这些少量的投影(或称测量值)中以高概率重构出原信号。
在压缩感知理论的框架下,采样率不决定于原始信号的带宽,而取决于重要信息在信号中的结构和内容,测量值并非是信号的本身,而是从高维到低维的投影值,每个测量值都包含了所有样本信号的少量信息,恢复信号所需测量值的数目远少于采样定理要求的数目。
对于一个N*1维信号s,其中s中包含K个非零元素,信号s经过公式(1)变换得到N*1维变量x,再经过公式(2)得到M*1维测量信号y,压缩感知的目的就是通过测量信号y重构出信号s。
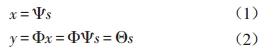
其中,Ψ为N*N维稀疏变换矩阵,Φ为M*N维测量矩阵(也称为投影矩阵或随机采样矩阵),Ψ、Φ的设计会严重影响压缩感知技术的性能,K
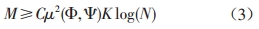
其中,μ2(Φ,Ψ)表示矩阵Ψ、Φ的相关性。
信号重构是压缩感知技术的核心,是一个在获得观测值y的条件下,寻求最稀疏解s的过程,这里需要引入矩阵理论中的范数概念来描述压缩感知理论的信号重构问题。
定义向量Z={z1,z2,…,zN}的P-范数为:
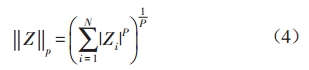
当p=0时得到向量Z的0-范数,表示Z中非零元素的个数。
通常情况下,对于一个非稀疏的信号x在经过稀疏化变换得到s的情况下,压缩感知理论中信号恢复问题,转化为线性约束下的最小0-范数的问题,可以用公式(5)表达:
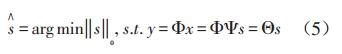
对上述0-范数的优化问题,是一个非凸优化问题,也就是在多项式内无法求解,更不能验证解的有效性,因此需要转换成其他范数,比如1-范数或2-范数,研究证明对于公式(5)最小0-范数问题可以通过求解一个更加简单的1-范数最优化问题得到与0-范数同等的解。因此,压缩感知理论通常用公式(6)描述:
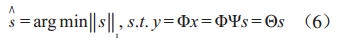
针对公式(6)的求解可以用线性规划算法等最优化理论实现,实际实现时也可以使用其他快速优化算法。
2 应用分析
压缩感知应用特征包括:
(1)观测信号不具有稀疏性,例如OFDM系统频域信道响应或线性阵列响应。
(2)通过对观测信号的基坐标变换,在另外一组基底下,信号变得稀疏,例如频域信道响应通过DFT变换之后,在时域具有稀疏性。
(3)稀疏性(稀疏位置)具有不可知与变化的特性,这是应用压缩感知的必要条件,如果稀疏位置具有可知性或恒定性。
外场测试表明,大部分无线信道在时域上一般都是多径稀疏的,根据压缩感知理论,这种稀疏性意味着可以大幅度地降低用户专有导频开销。
另外,随着基站侧天线数目增加,无线信道在空域上也同样体现出稀疏性,这意味着通过压缩感知技术可以有效减少小区公有导频的开销。
2.1 用户专有导频设计
根据压缩感知理论,再根据公式(6)可知,具有稀疏性的时域无线信道系数可以由在频域中少量分布的导频观测信号通过压缩感知技术恢复出来。
在未来移动通信系统的用户专有导频设计中,基于压缩感知技术,需要考虑的问题有:
(1)导频数目:估计信道的稀疏度K,然后利用公式(3)大概算一下需要的导频符号的数目m。
(2)导频位置:由测量矩阵决定,设计时一定要保证其随机性,可以根据小区标识、帧号、子帧号、资源位置作为随机矩阵生成因子,获取足够稀疏的导频位置,或者在标准化时预定义若干组随机导频位置,调度时根据系统参数确定使用哪一组随机导频位置,这与现有的LTE系统是明显不同的,现有系统中导频是均匀分布的,其间隔主要考虑了相关带宽。
(3)变换矩阵:优先考虑离散傅里叶变换矩阵。
(4)信号重构:接收方按照图1所示的流程,利用少量的频域导频信道值y,恢复时域信道h,其中目标函数最优化可以使用实现复杂度较低的Stomp算法。

图1 压缩感知技术的信号重构流程

图2 基于压缩感知技术导频设计仿真性能
图2给出了基于压缩感知技术进行用户专有导频设计后与传统的LTE导频相比的性能,图2为在扩展城市环境信道模型(ETU)场景、10MHz、16QAM下的符号差错率(SER)比较,其中LS-Ⅰ-6代表LTE标准导频模式,时域不做基于CP的截断处理,子载波间隔为6的仿真参数设置下的仿真结果;LS-Π-6代表LTE标准导频模式,时域做基于CP的截断处理,子载波间隔为6的仿真参数设置下的仿真结果;CS-Ⅰ-6代表压缩感知导频模式,时域不做基于CP的截断处理,子载波开销与LTE导频开销相同的仿真参数设置下的仿真结果;CS-Π-6代表压缩感知导频模式,时域做基于CP的截断处理,子载波开销与LTE导频开销相同的仿真参数设置下的仿真结果;CS-Ⅰ-12代表压缩感知导频模式,时域不做基于CP的截断处理,子载波开销是LTE导频开销一半的仿真参数设置下的仿真结果;CS-Π-12代表压缩感知导频模式,时域做基于CP的截断处理,子载波开销是LTE导频开销一半的仿真参数设置下的仿真结果。图2(a)给出了在LTE标准相同导频开销的条件下压缩感知技术的导频设计的性能,图2(b)给出了在只有LTE标准导频开销一半的条件下压缩感知技术的导频设计的性能。从仿真结果可以看出,基于压缩感知技术设计的导频可以有效降低系统开销,并提升接收方的解码能力。
2.2 小区公有导频设计
在大规模天线阵列系统中,基站侧天线数目增加,带来了小区公有导频开销的增加,会严重影响未来移动通信系统的性能,因此寻求一种基于低导频密度的信道估计方法变得非常必要。
随着基站侧天线数目增加,信道在空域上是否存在稀疏性是需要首先验证的问题。
图3给出了对基站配置128根天线形成的瞬时信道进行离散傅立叶变换(DFT)后得到的角度域功率谱分布情况,可以看出,变换后得到的变量是具有稀疏性的,因此可以通过压缩感知技术设计未来移动通信系统中的小区公有导频。

图3 128根天线信道的角度域功率谱分布
小区间公有导频设计导频数目、导频位置、信号重构可参考用户专有导频设计的思路,变换矩阵设计有两种方式:
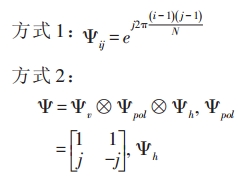
式中Ψ是DFT矩阵。
基于方式1和方式2进行小区间公有导频设计的仿真结果如图4所示。图4为累计分布函数,不考虑干扰/噪声。

图4 不同变换矩阵空域压缩感知性能分析
可以看出,两种方式都可以比较好地通过压缩感知技术重建空域信道,当随机采样点数目比较多时,两种变换矩阵重建信道时性能差别不大,但是当随机采样点数比较少时,方式2可以更好地重建信道,主要原因在于方式2提供的变换矩阵更好地体现了天线之间的相关性。
3 结束语
通过理论分析及大量仿真,证明了压缩感知技术可以有效地降低系统导频开销,提升系统性能。
后续也可以考虑将压缩感知技术与未来移动通信系统中可能使用的认知无线电技术结合起来用于发现空闲频谱比较多的频段内的空闲资源,有效降低系统硬件实现成本,或者是将压缩感知技术与其他天线降维技术结合起来,提升未来移动通信系统的用户体验。

 举报
举报

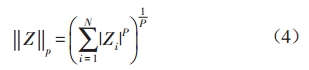



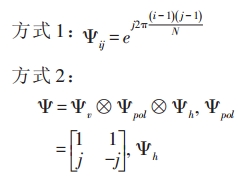


 举报
举报

