引言
无线传感器网络是由密集型、低成本、随机分布的节点组成,集成了传感器技术、计算机技术和通信技术,能够协同地实时监测、感知并采集各种环境的数据,适用于战场通信、抢险救灾和公共集会等突发性、临时性场合。保持节点之间时间上的同步在无线传感器网络中非常重要,它是保证可靠的数据传输、精确的节点定位、可靠的数据融合、准确的目标跟踪与检测的前提。如利用波的到达时间差测距,就需要高精度的时间同步。无线传感器网络中,由于频率漂移,各个节点之间必然会产生一定的时钟偏移,因此有效的时间同步技术对保证各个节点之间的时钟同步非常重要。
2002年,Elson等人在影响未来网络研究发展方向的国际权威学术会议HotNets上,首次提出无线传感器网络时间同步的研究课题,至今已有相当多的典型时间同步算法。基于发送者接收者的双向同步算法中,比较典型的如TPSN(Timingsync Protocol for Sensor Networks)算法。TPSN算法分成两个阶段,第一阶段为层次发现阶段,第二阶段为同步阶段。在同步阶段采用发送者接收者的双向成对同步算法, MAC层采用加入时间戳的技术,进而估算出节点之间的传输延迟与时钟偏移。该作者在Mica 节点上测试过,TPSN平均单跳误差为17.61 μs。基于发送者接收者的单向时间同步算法中,比较典型的如FTSP(Flooding Time Synchronization Protocol)算法、DMTS(Delay Measurement Time Synchronization)算法。基于接收者接收者的同步算法,典型的有RBS(Reference Broadcast Synchronization)算法。近几年,也有作者提出了协作同步机制。协作同步的核心思想仍然是属于集中式协议,要求整个网络中节点密度较高。作者提出了分步式同步机制,整个网络无需构造由根节点发起的生成树,只需要每个节点之间使用分布式广播同步机制。
传统的同步机制只是简单地修正节点之间的时钟偏移,传感器节点时钟由晶体振荡器驱动。晶体振荡器的实际频率通常与它标定的频率之间存在一定的偏移,即存在时钟频率的漂移。传统的同步算法为了提高同步精度,节点就必须频繁地重复时间同步算法,以消除时钟偏移的影响。频繁地交换消息,必然给功耗受限的节点带来额外的负担,因此考虑节点之间的时钟漂移也是非常重要的。
1 CDCO时钟同步算法设计
1.1 时钟模型
本同步算法采用的是发送者接收者的双向同步算法,同时考虑了时钟漂移与偏移对同步精度的影响。在无线传感器网络的节点中,如果采用的是时钟速率恒定模型,那么节点的硬件时钟Ci(t)与真实时间Ck(t)的关系可以表示为Ci(t)=aik·Ck(t)+mik。式中,aik为节点之间的相对漂移量,mik为节点之间的相对偏移量。如果两个节点之间完全同步,则相对漂移量aik为1,相对偏移量mik为0。
1.2 单跳同步原理
如图1所示,hi(t1)、hi(t4)、hi(t5)用来记录参考节点的本地时间, hk(t2)、hk(t3)、hk(t6)用来记录同步节点的本地时间。同步过程采用类似TPSN算法的双向同步过程,假设同步节点与参考节点的时钟关系采用时钟恒定模型(这在现实中也是合理的),则hk(t)=ρki·hi(t)+mki。式中,hk(t)、hi(t)分别为同步节点与参考节点在本地时刻t的时钟,ρki、mki分别为时钟漂移量与偏移量。
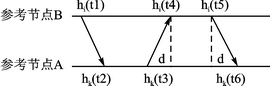
图1 双向同步原理图
假设传播延迟为dki,因为在极短的时间内来回传播延迟与节点时偏可假设相同。假设漂移量
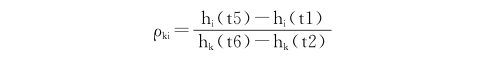
则在理想情况下,ρki为1,即线段hi(t1)hk(t2)平行于线段hi(t5)hk(t6),此时不存在时钟漂移[10]。如图1所示,根据双向同步原理与时钟恒定模型可以得到:
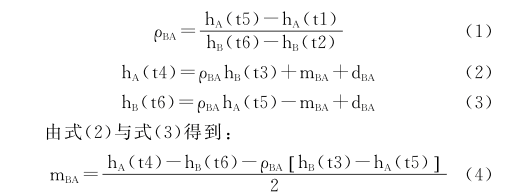
则根据得到的ρBA、mBA修改同步节点的本地时钟,就能实现与同步节点的时钟同步。
1.3 多跳同步原理
假设节点A与其下一跳节点B已经实现了时间同步,则可以得到:
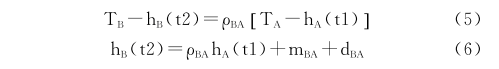
由式(5)与式(6)可以得到:
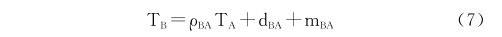
同样,假设节点B与下一跳节点C已经实现了时间同步,同理可以得到:
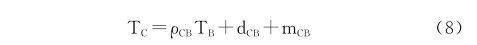
显然将式(7)带入式(8)可以得到节点A与C之间的同步。
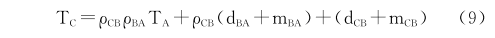
采用同样的方法逐级迭代下去,就可以实现全网的时间同步。
1.4 理论误差来源分析
由1.2节的分析可知,两节点之间的时钟关系为hk(t)=ρki·hi(t)+mki。如果两个节点不存在时钟频偏的情况,ρki为1,即hi(t1)hk(t2)平行于边hi(t5)hk(t6),则频率偏移误差:
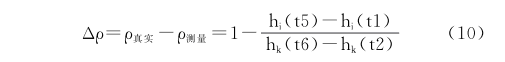
假设不存在频率偏移的情况下,即ρki为1,我们来计算时钟偏移的误差来源。根据图1所示的发送接收双向消息同步过程,可以得到:
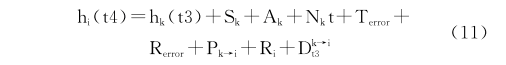
式中, hk(t3)、hi(t4)分别是t3、t4所对应的同步节点和本地节点所测出的本地时间,Sk代表节点k的报文发送时间,Ak是发送报文的访问时间,Pk→i是节点k传播到节点i的时间,Ri是节点i的报文接收处理时间,Nkt是传输Nk个比特的总时间,Terror指传输比特的误差,Rerror为打时标过程存在的误差,Dk→it3代表节点k与节点i在hk(t3)时刻的时偏。因为在实验中采用了MAC层的打时标方法,这样就可以消除发送时间与访问时间对误差的影响。于是式(11)就可以简写为:
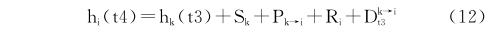
式中,Dk→it3=Dk→it6+RDk→it3→t6。同理可以得到hk(t6):

由以上各式可以得到时偏:
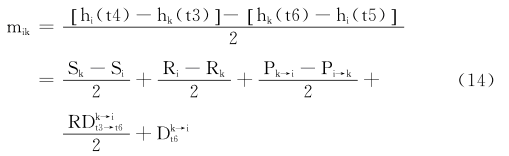
式中,RDk→it3→t6代表从hk(t3)到hk(t6)时段内,节点k相对于节点i增加的时偏;Dk→it6是hk(t6)时刻节点k与节点i之间的时偏。可以算出时钟偏差为:
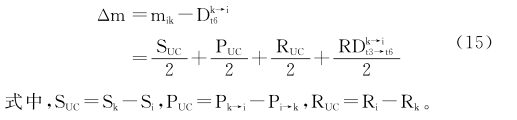
2 算法性能分析
无线传感器节点采用的是晶体振荡器来计时节点的本地时钟,由于成本的限制,只能采用一些低成本的晶振。硬件设备厂商一般都会给出晶振频率变化范围,一般时钟漂移为[10,100]ppm。同步周期取20 s,在一个周期内采样4次,得到的结果如表1所列。相同情况下的多跳同步误差如表2所列。

从表1中可以看出,在同一个周期内,相比TPSN算法,CDCO算法误差随采样间隔的增长明显比TPSN慢,在相同的采样间隔,误差也明显低于TPSN算法。因为相比于TPSN算法,本文考虑了时钟漂移,因此可以在较长的时间内保持同步。从表2可以看出,随跳数增加,CDCO算法精度较高于TPSN算法。在相同的跳数内,CDCO算法的误差明显低于TPSN算法,且随着跳数增加,CDCO算法的同步误差增加明显低于TPSN算法。相对于TPSN算法,CDCO算法可以减小误差多跳累加的影响。
结语
本文基于发送方接收方双向同步算法的原理,设计了一种同时考虑时钟偏移与漂移的同步补偿机制(CDCO算法)。实验结果表明,相比传统的发送方接收方双向同步算法,CDCO算法因为采用了时钟漂移补偿技术,在同一个同步周期内,同步误差随时间增加变化较小;而传统的算法因为存在时钟漂移,在同一个周期内误差随时间增大而变得越来越大。相对于TPSN算法,CDCO算法可以减小误差多跳累加的影响。
引言
无线传感器网络是由密集型、低成本、随机分布的节点组成,集成了传感器技术、计算机技术和通信技术,能够协同地实时监测、感知并采集各种环境的数据,适用于战场通信、抢险救灾和公共集会等突发性、临时性场合。保持节点之间时间上的同步在无线传感器网络中非常重要,它是保证可靠的数据传输、精确的节点定位、可靠的数据融合、准确的目标跟踪与检测的前提。如利用波的到达时间差测距,就需要高精度的时间同步。无线传感器网络中,由于频率漂移,各个节点之间必然会产生一定的时钟偏移,因此有效的时间同步技术对保证各个节点之间的时钟同步非常重要。
2002年,Elson等人在影响未来网络研究发展方向的国际权威学术会议HotNets上,首次提出无线传感器网络时间同步的研究课题,至今已有相当多的典型时间同步算法。基于发送者接收者的双向同步算法中,比较典型的如TPSN(Timingsync Protocol for Sensor Networks)算法。TPSN算法分成两个阶段,第一阶段为层次发现阶段,第二阶段为同步阶段。在同步阶段采用发送者接收者的双向成对同步算法, MAC层采用加入时间戳的技术,进而估算出节点之间的传输延迟与时钟偏移。该作者在Mica 节点上测试过,TPSN平均单跳误差为17.61 μs。基于发送者接收者的单向时间同步算法中,比较典型的如FTSP(Flooding Time Synchronization Protocol)算法、DMTS(Delay Measurement Time Synchronization)算法。基于接收者接收者的同步算法,典型的有RBS(Reference Broadcast Synchronization)算法。近几年,也有作者提出了协作同步机制。协作同步的核心思想仍然是属于集中式协议,要求整个网络中节点密度较高。作者提出了分步式同步机制,整个网络无需构造由根节点发起的生成树,只需要每个节点之间使用分布式广播同步机制。
传统的同步机制只是简单地修正节点之间的时钟偏移,传感器节点时钟由晶体振荡器驱动。晶体振荡器的实际频率通常与它标定的频率之间存在一定的偏移,即存在时钟频率的漂移。传统的同步算法为了提高同步精度,节点就必须频繁地重复时间同步算法,以消除时钟偏移的影响。频繁地交换消息,必然给功耗受限的节点带来额外的负担,因此考虑节点之间的时钟漂移也是非常重要的。
1 CDCO时钟同步算法设计
1.1 时钟模型
本同步算法采用的是发送者接收者的双向同步算法,同时考虑了时钟漂移与偏移对同步精度的影响。在无线传感器网络的节点中,如果采用的是时钟速率恒定模型,那么节点的硬件时钟Ci(t)与真实时间Ck(t)的关系可以表示为Ci(t)=aik·Ck(t)+mik。式中,aik为节点之间的相对漂移量,mik为节点之间的相对偏移量。如果两个节点之间完全同步,则相对漂移量aik为1,相对偏移量mik为0。
1.2 单跳同步原理
如图1所示,hi(t1)、hi(t4)、hi(t5)用来记录参考节点的本地时间, hk(t2)、hk(t3)、hk(t6)用来记录同步节点的本地时间。同步过程采用类似TPSN算法的双向同步过程,假设同步节点与参考节点的时钟关系采用时钟恒定模型(这在现实中也是合理的),则hk(t)=ρki·hi(t)+mki。式中,hk(t)、hi(t)分别为同步节点与参考节点在本地时刻t的时钟,ρki、mki分别为时钟漂移量与偏移量。

图1 双向同步原理图
假设传播延迟为dki,因为在极短的时间内来回传播延迟与节点时偏可假设相同。假设漂移量
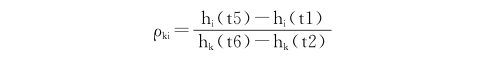
则在理想情况下,ρki为1,即线段hi(t1)hk(t2)平行于线段hi(t5)hk(t6),此时不存在时钟漂移[10]。如图1所示,根据双向同步原理与时钟恒定模型可以得到:
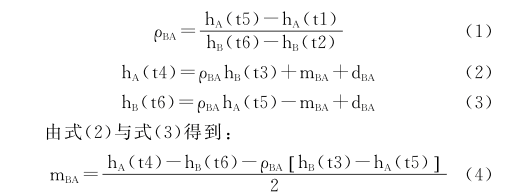
则根据得到的ρBA、mBA修改同步节点的本地时钟,就能实现与同步节点的时钟同步。
1.3 多跳同步原理
假设节点A与其下一跳节点B已经实现了时间同步,则可以得到:
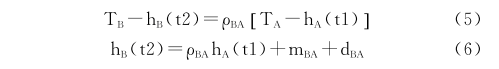
由式(5)与式(6)可以得到:
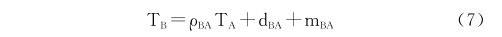
同样,假设节点B与下一跳节点C已经实现了时间同步,同理可以得到:
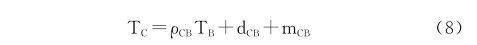
显然将式(7)带入式(8)可以得到节点A与C之间的同步。
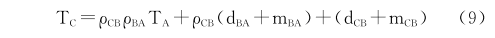
采用同样的方法逐级迭代下去,就可以实现全网的时间同步。
1.4 理论误差来源分析
由1.2节的分析可知,两节点之间的时钟关系为hk(t)=ρki·hi(t)+mki。如果两个节点不存在时钟频偏的情况,ρki为1,即hi(t1)hk(t2)平行于边hi(t5)hk(t6),则频率偏移误差:
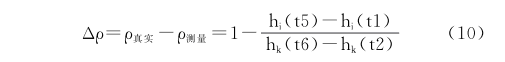
假设不存在频率偏移的情况下,即ρki为1,我们来计算时钟偏移的误差来源。根据图1所示的发送接收双向消息同步过程,可以得到:
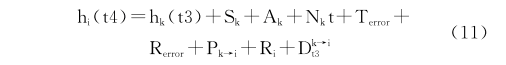
式中, hk(t3)、hi(t4)分别是t3、t4所对应的同步节点和本地节点所测出的本地时间,Sk代表节点k的报文发送时间,Ak是发送报文的访问时间,Pk→i是节点k传播到节点i的时间,Ri是节点i的报文接收处理时间,Nkt是传输Nk个比特的总时间,Terror指传输比特的误差,Rerror为打时标过程存在的误差,Dk→it3代表节点k与节点i在hk(t3)时刻的时偏。因为在实验中采用了MAC层的打时标方法,这样就可以消除发送时间与访问时间对误差的影响。于是式(11)就可以简写为:
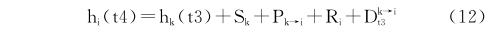
式中,Dk→it3=Dk→it6+RDk→it3→t6。同理可以得到hk(t6):

由以上各式可以得到时偏:
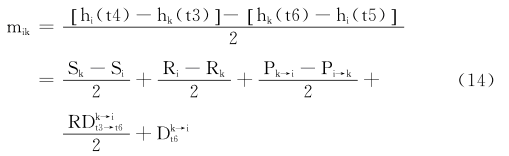
式中,RDk→it3→t6代表从hk(t3)到hk(t6)时段内,节点k相对于节点i增加的时偏;Dk→it6是hk(t6)时刻节点k与节点i之间的时偏。可以算出时钟偏差为:
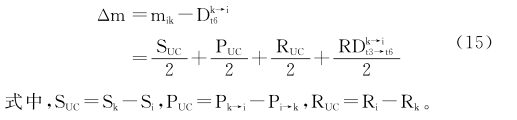
2 算法性能分析
无线传感器节点采用的是晶体振荡器来计时节点的本地时钟,由于成本的限制,只能采用一些低成本的晶振。硬件设备厂商一般都会给出晶振频率变化范围,一般时钟漂移为[10,100]ppm。同步周期取20 s,在一个周期内采样4次,得到的结果如表1所列。相同情况下的多跳同步误差如表2所列。

从表1中可以看出,在同一个周期内,相比TPSN算法,CDCO算法误差随采样间隔的增长明显比TPSN慢,在相同的采样间隔,误差也明显低于TPSN算法。因为相比于TPSN算法,本文考虑了时钟漂移,因此可以在较长的时间内保持同步。从表2可以看出,随跳数增加,CDCO算法精度较高于TPSN算法。在相同的跳数内,CDCO算法的误差明显低于TPSN算法,且随着跳数增加,CDCO算法的同步误差增加明显低于TPSN算法。相对于TPSN算法,CDCO算法可以减小误差多跳累加的影响。
结语
本文基于发送方接收方双向同步算法的原理,设计了一种同时考虑时钟偏移与漂移的同步补偿机制(CDCO算法)。实验结果表明,相比传统的发送方接收方双向同步算法,CDCO算法因为采用了时钟漂移补偿技术,在同一个同步周期内,同步误差随时间增加变化较小;而传统的算法因为存在时钟漂移,在同一个周期内误差随时间增大而变得越来越大。相对于TPSN算法,CDCO算法可以减小误差多跳累加的影响。

 举报
举报


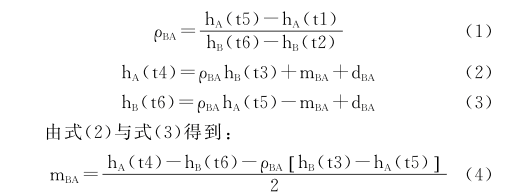
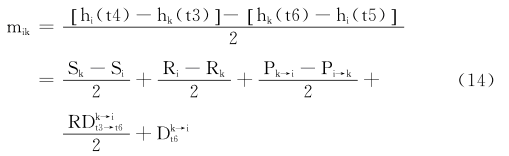
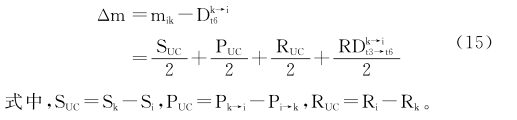


 举报
举报

