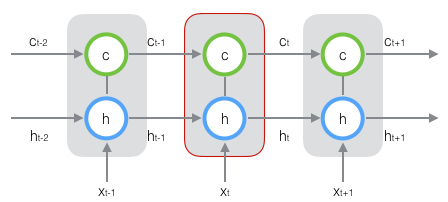
长短时记忆网络的前向计算
我们引入“门(gate)”的概念。门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。假设W是门的权重向量,bb是偏置项,那么门可以表示为:σg(x)=σ(Wx+b)g(x)=σ(Wx+b)
门的输出是0到1之间的实数向量,用门向量的输出向量按元素乘以我们需要控制的那个向量,当门输出为0时,任何向量与之相乘都会得到0向量,这就相当于啥都不能通过;输出为1时,任何向量与之相乘都不会有任何改变,这就相当于啥都可以通过。因为σσ(也就是sigmoid函数)的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c的内容,一个是遗忘门,它决定了上一时刻的单元状态ct−1ct−1有多少保留到当前时刻ctct;另外一个是输出门,他决定了当前时刻网络的输入xtxt有多少保存到单元状态ctct。LSTM用输出门来控制单元状态ctct有多少输出到LSTM的当前输出值htht。LSTM用输出门来控制单元状态ctct有多少输出到LSTM的当前输出值htht。
遗忘门的表达式是:
athbfft=σ(Wf⋅[ht−1,xt]+bf)(式1)athbfft=σ(Wf⋅[ht−1,xt]+bf)(式1)
上式中,WfWf是遗忘门的权重矩阵,ht−1,xtht−1,xt表示把两个向量连接成一个更长的向量,bfbf是遗忘门的偏置项,σ是sigmoid函数。如果输入的维度是dx,隐藏层的维度是dh,单元状态的维度是dc(d_c=d_h),则遗忘门的权重矩阵Wf维度是dcx(dh+dx)。事实上,权重矩阵Wf都是两个矩阵拼接而成的:一个是Wfh,它对应着输入项ht−1,其维度为dcxdh;一个是Wfx,它对应着输入项xt,其维度为dcxdx。Wf可以写为:
[Wf][ht−1xt]=[WfhWfx][ht−1xt]=Wfhht−1+Wfxxt(1)(2)
下图显示了遗忘门的计算:

接下来看看输入门:
it=σ(Wi⋅[ht−1,xt]+bi)(式2)
上式中,Wi是输入门的权重矩阵,$b_i$是输入门的偏置项。下图表示了输入门的计算:

接下来,我们计算用于描述当前输入的单元状态c~t,它是根据上一次的输出和本次输入来计算的:
c~t=tanh(Wc⋅[ht−1,xt]+bc)(式3)
下图是c~t的计算:
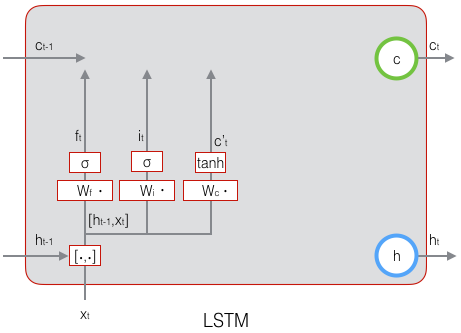
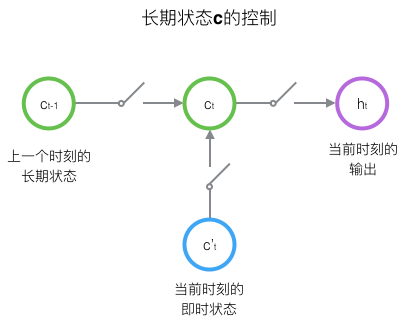
现在,我们计算当前时刻的单元状态ct。它是由上一次的单元状态ct−1按元素乘以遗忘门ft,再用当前输入的单元状态c~t按元素乘以输入门it,再将两个积加和产生的:
ct=ft∘ct−1+it∘c~t(式4)
符号O表示按元素乘。下图是ct的计算:
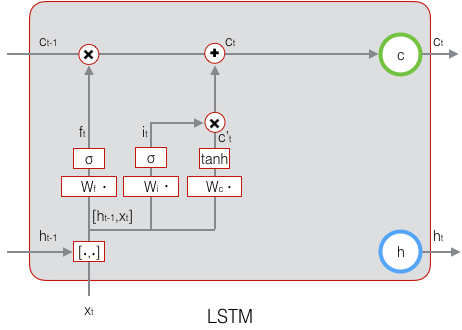
这样,我们就把LSTM关于当前的记忆c~t和长期的记忆ct−1组合在一起,形成了新的单元状态ct。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容进入记忆。下面,我们要看看输出门,它控制了长期记忆对当前输出的影响:
ot=σ(Wo⋅[ht−1,xt]+bo)(式5)
下面表示输出门的计算:
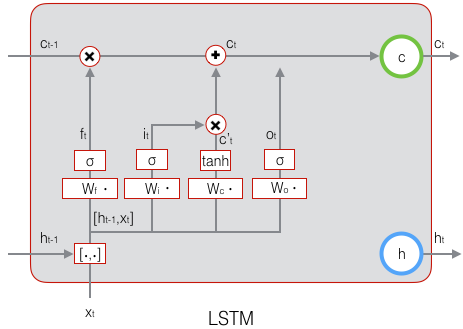
LSTM最终的输出,是由输出门和单元状态共同确定的:
ht=ot∘tanh(ct)(式6)
下图表示LSTM最终输出的计算:

式1到式6就是LSTM前向计算的全部公式。至此,我们就把LSTM前向计算讲完了。
长短时记忆网络的前向计算
我们引入“门(gate)”的概念。门实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量。假设W是门的权重向量,bb是偏置项,那么门可以表示为:σg(x)=σ(Wx+b)g(x)=σ(Wx+b)
门的输出是0到1之间的实数向量,用门向量的输出向量按元素乘以我们需要控制的那个向量,当门输出为0时,任何向量与之相乘都会得到0向量,这就相当于啥都不能通过;输出为1时,任何向量与之相乘都不会有任何改变,这就相当于啥都可以通过。因为σσ(也就是sigmoid函数)的值域是(0,1),所以门的状态都是半开半闭的。
LSTM用两个门来控制单元状态c的内容,一个是遗忘门,它决定了上一时刻的单元状态ct−1ct−1有多少保留到当前时刻ctct;另外一个是输出门,他决定了当前时刻网络的输入xtxt有多少保存到单元状态ctct。LSTM用输出门来控制单元状态ctct有多少输出到LSTM的当前输出值htht。LSTM用输出门来控制单元状态ctct有多少输出到LSTM的当前输出值htht。
遗忘门的表达式是:
athbfft=σ(Wf⋅[ht−1,xt]+bf)(式1)athbfft=σ(Wf⋅[ht−1,xt]+bf)(式1)
上式中,WfWf是遗忘门的权重矩阵,ht−1,xtht−1,xt表示把两个向量连接成一个更长的向量,bfbf是遗忘门的偏置项,σ是sigmoid函数。如果输入的维度是dx,隐藏层的维度是dh,单元状态的维度是dc(d_c=d_h),则遗忘门的权重矩阵Wf维度是dcx(dh+dx)。事实上,权重矩阵Wf都是两个矩阵拼接而成的:一个是Wfh,它对应着输入项ht−1,其维度为dcxdh;一个是Wfx,它对应着输入项xt,其维度为dcxdx。Wf可以写为:
[Wf][ht−1xt]=[WfhWfx][ht−1xt]=Wfhht−1+Wfxxt(1)(2)
下图显示了遗忘门的计算:

接下来看看输入门:
it=σ(Wi⋅[ht−1,xt]+bi)(式2)
上式中,Wi是输入门的权重矩阵,$b_i$是输入门的偏置项。下图表示了输入门的计算:

接下来,我们计算用于描述当前输入的单元状态c~t,它是根据上一次的输出和本次输入来计算的:
c~t=tanh(Wc⋅[ht−1,xt]+bc)(式3)
下图是c~t的计算:

现在,我们计算当前时刻的单元状态ct。它是由上一次的单元状态ct−1按元素乘以遗忘门ft,再用当前输入的单元状态c~t按元素乘以输入门it,再将两个积加和产生的:
ct=ft∘ct−1+it∘c~t(式4)
符号O表示按元素乘。下图是ct的计算:

这样,我们就把LSTM关于当前的记忆c~t和长期的记忆ct−1组合在一起,形成了新的单元状态ct。由于遗忘门的控制,它可以保存很久很久之前的信息,由于输入门的控制,它又可以避免当前无关紧要的内容进入记忆。下面,我们要看看输出门,它控制了长期记忆对当前输出的影响:
ot=σ(Wo⋅[ht−1,xt]+bo)(式5)
下面表示输出门的计算:

LSTM最终的输出,是由输出门和单元状态共同确定的:
ht=ot∘tanh(ct)(式6)
下图表示LSTM最终输出的计算:

式1到式6就是LSTM前向计算的全部公式。至此,我们就把LSTM前向计算讲完了。

 举报
举报


 举报
举报







 举报
举报

 举报
举报

