示波器的采样率和示波器存储深度

0

示波器的采样率和示波器存储深度

示波器的采样率和存储深度

在选择示波器时，工程师首先需要确定测量所需的带宽。然而当示波器的带宽确定后，影响实际测量的恰恰是相互作用、相互制约的采样率和存储深度。图1是数字示波器的工作原理简图。

ticle/UploadPic/2009-8/2009824235823534.jpg"/>

图1 数字存储示波器的原理组成框图

输入的电压信号首先进入示波器的前端放大器，放大器将信号放大或者衰减以调整信号的动态范围，其输出的信号由采样/保持电路进行采样，并由A/D转换器数字化。经过A/D转换后，信号变成数字形式存入存储器中，微处理器对存储器中的数字化信号波形进行相应的处理，并显示在显示屏上。这就是数字存储示波器简单的工作过程。

采样、采样速率
由于计算机只能处理离散的数字信号，模拟电压信号进入示波器后面临的首要问题就是连续信号的数字化（模/数转化）问题。

通过测量等时间间隔波形的电压幅值，并把该电压转化为用8位二进制代码表示的数字信息，这就是DSO的采样（见图2）。每两次采样之间的时间间隔越小，那么重建出来的波形就越接近原始信号。采样率（Sampling Rate）就是采样时间间隔的倒数。例如，如果示波器的采样率是每秒10G次（10GSa/s），则意味着每100ps进行一次采样。 

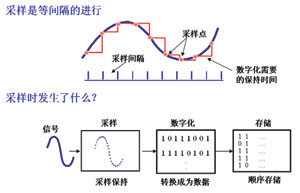
  图2 示波器的采样

根据Nyquist采样定理，对于正弦波，每个周期至少需要两次以上的采样才能保证数字化后的脉冲序列能较为准确的还原原始波形。如果采样率低于Nyquist采样率则会导致混叠（Aliasing）现象。

由Nyquist定理知道对于最大采样率为10GSa/s的示波器，可以测量最高频率为5GHz的信号，即采样率的一半，这就是示波器的数字带宽，而这个带宽是DSO的上限频率，实际带宽是不可能达到这个值的，数字带宽是从理论上推导出来的，是DSO带宽的理论值。与我们经常提到的示波器带宽（模拟带宽）是完全不同的两个概念。

那么在实际的测量中，对确定的示波器带宽，采样率到底选取多大？通常还与示波器所采用的采样模式有关。  

采样模式
采样技术大体上分为两类：实时模式和等效时间模式。

实时采样（Real-Time Sampling）模式用来捕获非重复性或单次信号，使用固定的时间间隔进行采样。触发一次后，示波器对电压进行连续采样，然后根据采样点重建信号波形。

等效时间采样（Equivalent-Time Sampling），是对周期性波形在不同的周期中进行采样，然后将采样点拼接起来重建波形，为了得到足够多的采样点，需要多次触发。等效时间采样又包括顺序采样和随机重复采样两种。使用等效时间采样模式必须满足两个前提条件：1.波形必须是重复的；2.必须能稳定触发。

示波器绝大部分时间工作在实时采样模式下，此时示波器的带宽取决于ADC的最高采样速率和所采用的内插算法。因此示波器的实时带宽与DSO采用的内插算法有关。

通常用有效存储带宽（BWa）来表征DSO的实际带宽,其定义为：BWa=最高采样速率/K。对于单次信号，最高采样速率是指最高实时采样速率，即A/D转化器的最高速率；对于重复信号，是指最高等效采样速率。K称为带宽因子，取决于DSO采用的内插算法。DSO采用的内插算法一般有线性（linear）插值和正弦（sinx/x）插值两种。K在用线性插值时约为10，用正弦内插约为2.5，而K=2.5只适用于重现正弦波，对于脉冲波，一般取K=4,此时，具有1GSa/s采样率的DSO的有效存储带宽为250MHz。这也解释了示波器用于实时采样时，为什么最大采样率通常是其额定模拟带宽的四倍或以上。一般来说，采样率总是越高越好。

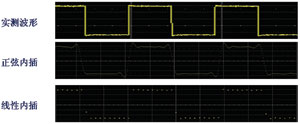
图3 不同插值方式的波形显示

存储、存储深度
在示波器中，把经过A/D数字化后的八位二进制波形信息存储到示波器的高速CMOS存储器中，就是示波器的存储。存储器的容量（存储深度）是很重要的。在存储深度一定的情况下，存储速度越快，存储时间就越短，它们之间是反比关系。所以：
存储深度＝采样率×采样时间

由此可见，提高示波器的存储深度可以间接提高其采样率：当要捕获较长的波形时，由于存储深度是固定的，所以只能降低采样率，但这样势必造成波形质量的下降；如果增大存储深度，则可以使用更高的采样率，以获取不失真的波形。

因此，存储深度决定了DSO同时分析高频和低频现象的能力，包括低速信号的高频噪声和高速信号的低频调制。

了解了采样率和存储深度后，就非常容易理解这两个参数对于实际测量的影响。

1 电源测量中长存储的重要性
在常见的开关电源的测试中，开关频率一般为200kHz左右或者更快，由于开关信号中经常存在工频调制，工程师需要捕获工频信号的四分之一周期或者半周期，甚至是多个周期。开关信号的典型上升时间约为100ns，为保证精确的重建波形需要在信号的上升沿上有5个以上的采样点，即采样率至少为5/100ns=50MSa/s，也就是两个采样点之间的时间间隔要小于100/5=20ns，对于至少捕获一个工频周期的要求，意味着需要捕获一段20ms长的波形，这样可以计算出来示波器每通道所需的存储深度=20ms/20ns=1M。同样，在分析电源上电的软启动过程中功率器件承受的电压应力的最大值则需要捕获整个上电过程（十几毫秒），所需要的示波器采样率和存储深度甚至更高。

2 存储深度对FFT结果的影响
在DSO中，通过快速傅立叶变换（FFT）可以得到信号的频谱，进而在频域对一个信号进行分析。如电源谐波的测量需要用FFT来观察频谱，在高速串行数据的测量中也经常用FFT来分析导致系统失效的噪声和干扰。

对于FFT运算，存储深度将同时决定可观察信号成分的最大范围（奈奎斯特频率）和频率分辨率△f。如果奈奎斯特频率为500MHz，分辨率为10kHz，若要获得10kHz的分辨率，则采集时间至少为：  
T=1/△f=1/10kHz=100ms

5