实现七位半DMM的要求到底有多高？

许多仪器仪表应用要求高准确度，例如数字万用表(DMM)、三相标准表、现场仪表校准器、高准确度DAQ系统、电子秤/实验室天平、地震物探仪以及自动测试设备(ATE)中的源表(SMU)/功率测量单元(PMU)等。这些应用需要以非常高的准确度测量直流或低频交流信号，大多数情况下，实现应用选择的相关元器件需具备低INL、高分辨率、良好的稳定性和可重复性。在所有这些应用中，DMM是最具代表性的应用。

为了构建七位半或更高准确度的DMM，业界通常采用基于分立元器件搭建的多斜率积分ADC。虽然此类ADC能够保证合理的测量准确度，但其设计和调试颇为复杂，因此许多工程师采用商用ADC IC来完成设计。在过去的十多年里，市场上的24位Σ-Δ ADC被广泛应用于六位半DMM的设计中。 要想实现七位半准确度和线性度，就必须使用更高性能的ADC。 另一个挑战来自基准电压源，深埋型齐纳二极管基准电压源需要复杂的外部信号调理电路才能实现超低温度漂移。

本文将介绍由低INL SAR ADC、全集成式超低温漂精密基准电压源、四通道匹配电阻网络和零漂移低噪声放大器构建的高准确度信号链解决方案。文中进行了准确度的理论分析和计算，可作为实际电路设计和测试的参考和指导。

高准确度DMM的主要直流指标参数

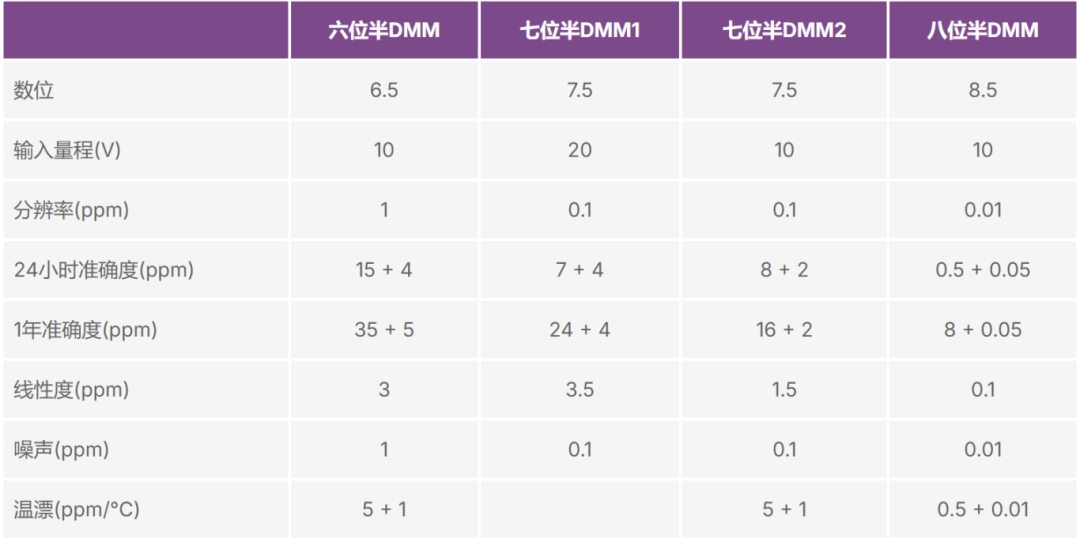
表1-1列出了市场上典型高准确度DMM的主要直流电压测量指标参数。主要的指标参数包括：

• 输入量程： 定义允许的输入信号范围。DMM的各项规格参数和输入量程有关，输入量程有1000 V、100 V、10 V、1 V或100 mV等。10 V为典型输入量程，此时DMM的各项参数性能较优。表1-1为10 V量程对应的各项指标参数。对于其他量程，可使用高准确度电阻将1000 V或100 V信号衰减至10 V量程，或者使用匹配良好的电阻阵列将1 V或100 mV信号放大至10 V量程。
• 分辨率或位数： 分辨率通常以百分比、ppm、或位数来表示。
• DMM的分辨率大多根据所显示的数字位数(数位)来指定。通常，这可能是由一个整数和0.5组成的数字，例如六位半。半位可以显示0或1。
• 典型的六位半表在1 V测量量程最高可以显示1.199999。典型的七位半仪表在10 V测量量程最高可以显示11.999999。
• 对于某些产品，例如ADC，分辨率通常以位数来表示。例如，24位ADC会提供2^24个不同的值，即16777216个值。分辨率用数位表示为lg(16777216) = 7.2。请注意，24位ADC的有效分辨率通常小于24位，这意味着其有效数位小于7.2。
• 准确度： 准确度用于衡量测量结果与真实值之间的一致程度。
• 许多因素都会影响准确度，例如噪声、失调误差、增益误差和线性度等。就模拟信号链而言，信号链上的每个元器件都有这些误差，并且可能影响整个系统的误差或准确度。
• 准确度指标可能随温度和时间而变化。24小时准确度、1年准确度和温漂可用于描述随时间和温度变化的准确度性能。这些参数决定了设备的稳定性和可重复性，即测量值是否随时间变化以及多次测量值是否一致。
• 表1-1中的准确度是在100 PLC或10 PLC (5 Hz)的读取速率下测试的，其中，PLC是工频周期，100 PLC表示一个测量周期为100/50 Hz，即2秒。
• 线性度： 用于衡量设备的输入和输出的线性关系。线性度可能会影响系统的准确度。
• 噪声： 系统噪声决定了DMM设备的最低有效数位。通常，此参数在100 PLC或10 PLC下进行测试。
• 对于表1-1中所示的七位半DMM2，10 V输入量程0.1 ppm，则噪声为1 μVrms。这意味着，当输入端短路时，最低数位(1 μV)读数可能会发生变化，读数值为00.00000X（X会变化）。

对于高准确度信号链，信号链上的转换器、基准电压源、精密放大器和匹配电阻网络都会影响系统噪声和准确度。更多细节将在后续章节中讨论。

表1-1. 市场上的高准确度DMM

ADC

ADC用于将模拟信号转换为数字码，是模拟域和数字域之间的桥梁。

表1-2列出了10 V输入量程下不同DMM的ADC有效分辨率要求。请注意，市场上大多数DMM的实际分辨率数位均小于理想分辨率数位。例如，七位半DMM2的实际分辨率为7.1数位（DMM显示范围为12000000），ADC有效分辨率至少需要为24.5位（考虑到信号有正负，2的24.5次幂= 23726566，接近24000000），10 V输入量程的噪声应小于1 μV rms。

表1-2. DMM 对ADC有效分辨率的要求

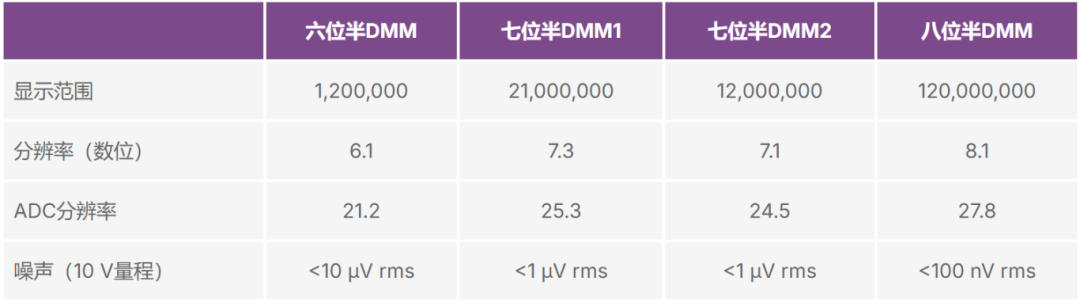
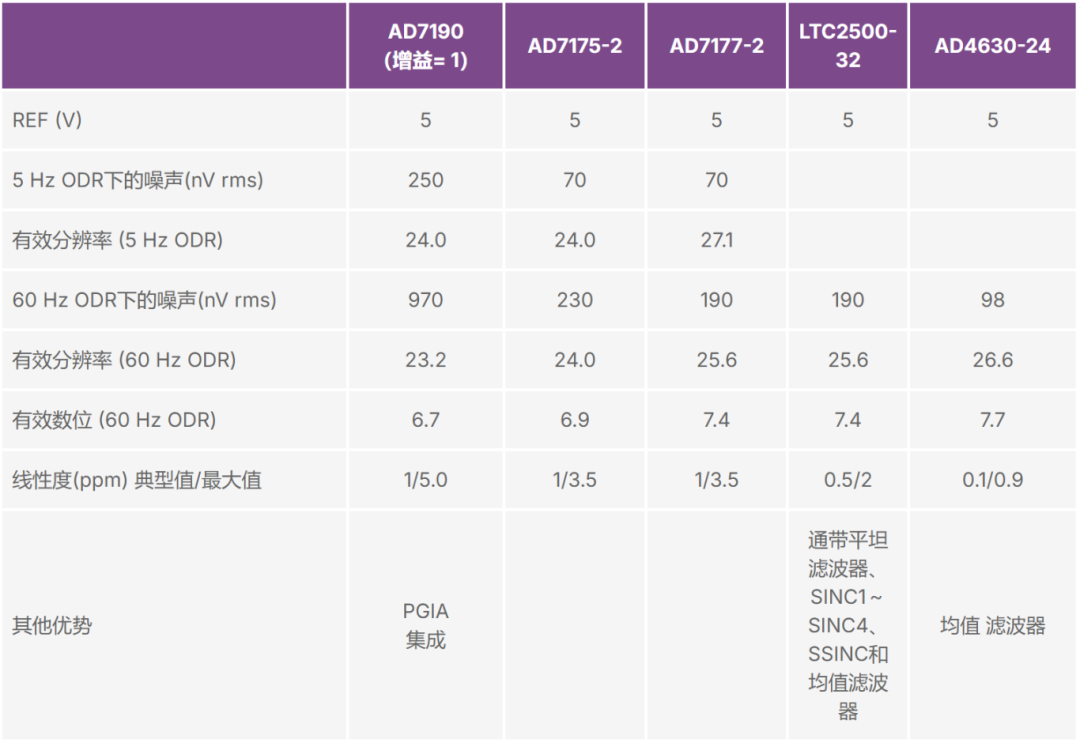
表1-3列出了ADI公司高分辨率ADC的噪声指标和有效分辨率。

• 对于六位半应用， AD7190 和 AD7175-2是很好的ADC选择。
• 对于七位半应用， AD7177-2 和LTC2500-32是很好的ADC选择。
• AD4630-24的INL为±0.1 ppm典型值（±0.9 ppm最大值），显著优于其他ADC。双通道、同步采样、2 MSPS SAR ADC AD4630-24同时具有低噪声、低零漂和低增益温漂特性，是七位半信号链解决方案的最佳选择。
• AD4030-24是单通道2 MSPS ADC， AD4632-24是双通道500 kSPS ADC， AD4032-24是单通道500 kSPS ADC。所有这些器件的INL性能都相似，单通道器件的噪声性能更优。

表1-3. ADI高分辨率ADC的噪声和分辨率指标

基准电压源

基准电压源决定了系统准确度。温漂(TC)、时漂(LTD)、噪声和初始准确度是基准电压源的主要指标参数。

LTZ1000和LM399具有良好的温漂和时漂指标参数，已经被广泛应用于高数位DMM。支持高准确度的基准电压源还有很多选择：

• ADR1399的噪声和负载调整指标优于LM399。
• ADR1001是一款完全集成、超低温漂、深埋型齐纳二极管精密 基准电压源。ADR1001将LTZ1000所需的整个信号调理电路集成到单个芯片中，使得整体解决方案面积显著减小，这简化了设计流程。
• ADR4550D输出电压为5V，初始准确度高。D级的温漂和时漂指标参数优于A/B/C级。

所有这些基准电压源都是高准确度信号链的出色选择。

表1-4. 基准电压源指标比较表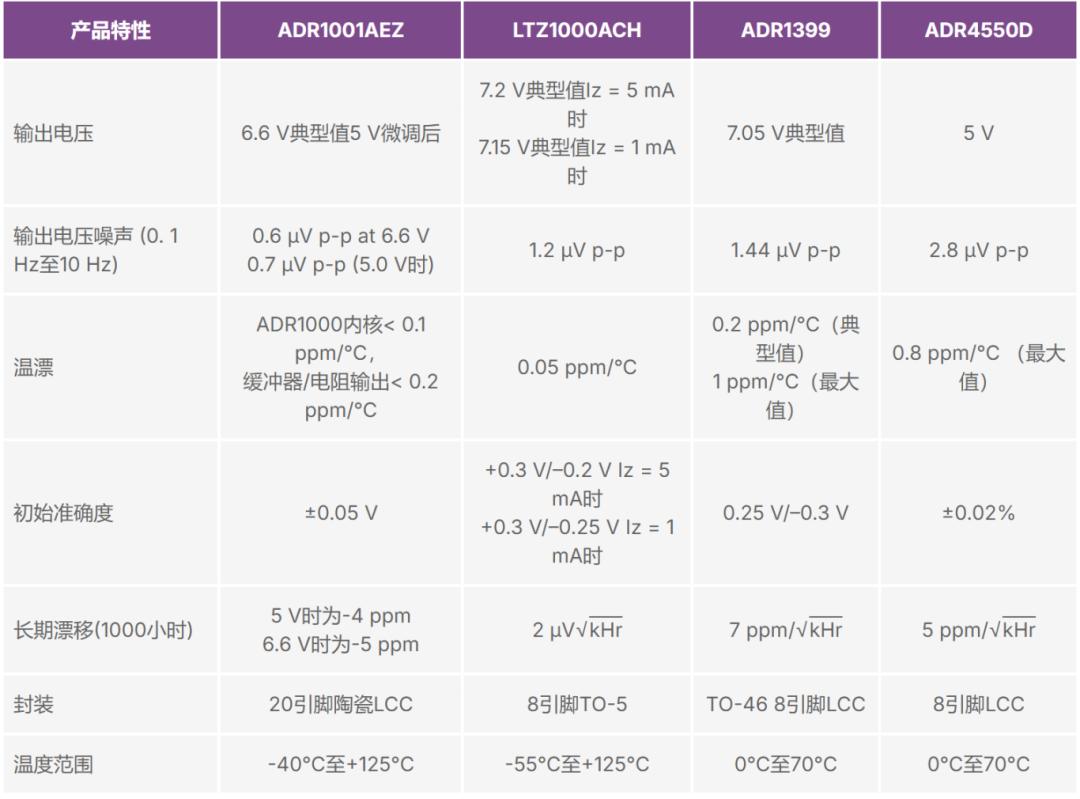

放大器

许多运算放大器的某些误差指标在ppm量级，但没有一个运算放大器的所有误差指标都能达到ppm量级。例如，斩波放大器可提供ppm级的失调电压、DC线性度和低频噪声，但其输入偏置电流和线性度随频率误差较大。双极性放大器具有低宽带噪声和良好的线性度，但其输入电流仍可能导致内部电路误差。MOS放大器具有出色的偏置电流，但通常在低频噪声和线性度方面存在缺陷。

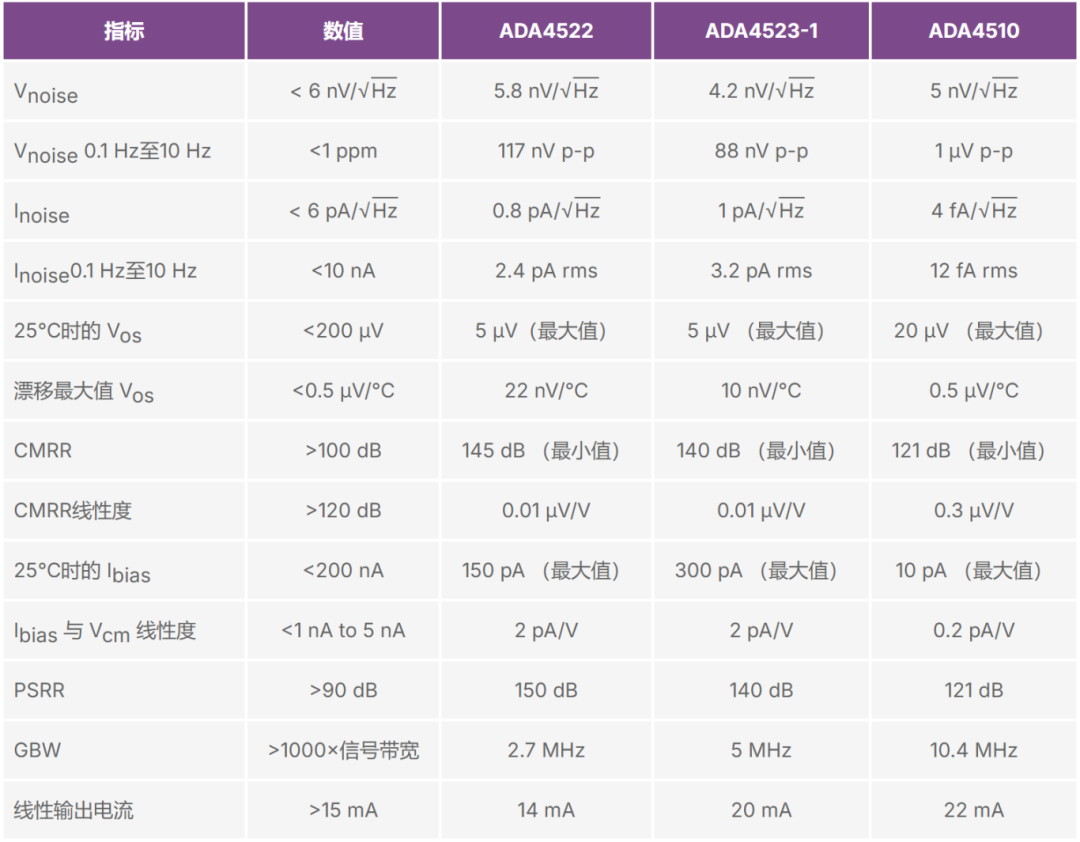
在实际电平搬移、衰减/放大和有源滤波器电路中，要满足±5 V信号、适用于1 kΩ环境并达到1 ppm线性度，运算放大器需满足一些基本要求，如表1-5第二列所示。

除了表1-5列出的参数外，温漂和时漂也非常重要。ADA4522-2和ADA4523-1采用自校准电路，具有低温漂（最大0.01 µV/°C）以及低 时漂。

对于目标信号频率接近斩波放大器开关频率的应用，ADA4510-2可能是个好的选择，其大多数指标都足够好，可以用在信号链的任何位置。

表1-5. ppm准确度所需的运算放大器指标及数值列表

匹配电阻网络

匹配电阻网络 LT5400和 LT5401具有非常低的匹配温漂和时漂指标，可与放大器配合使用，根据不同应用的要求配置模拟前端的增益。表1-6为ADI公司的匹配电阻网络产品。对于LT5400，表中列出的是B级指标。LT5400 A级的绝对电阻匹配比更优，其匹配温漂和时漂与LT5400B相同。

表1-6. 匹配电阻网络

AFE电路（增益固定）

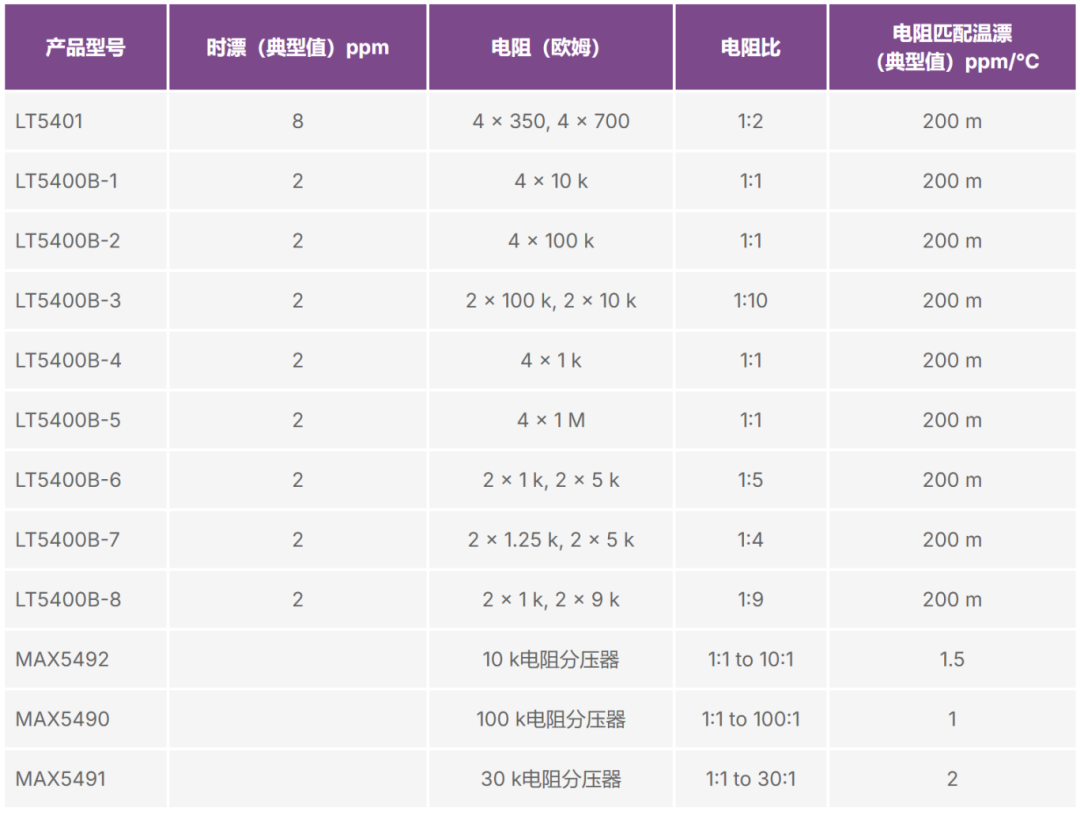
图1-1是 LTspice® AFE电路，将±10 V信号转换为ADC容许输入范围内的2.5 V ± 2.5 V差模信号。

• U1和U3是缓冲器，用于增加AFE电路的输入阻抗。
• VCOM提供2.5 V电压，将AFE输出偏置为正信号。
• LT5400-7（2×1.25k、2×5k）将信号衰减1/4，以使信号处于ADC输入范围内。
• 放大器配置为环路内补偿电路，以驱动SAR ADC。
• 蓝色曲线（±10 V输入）和红色曲线（±5 V差分输出）是LTspice的仿真结果。

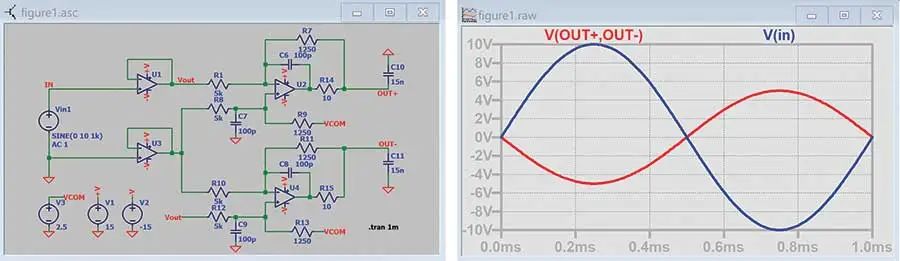
图1-1. LTspice AFE电路

0.1 Hz至～10 Hz时，AFE电路的噪声仿真结果为32 nV rms，大概是98 nV rms ADC噪声的1/3。

24小时准确度分析(Ta = 23 ± 1°C)

影响准确度的主要因素是两类误差：失调误差和增益误差。失调误差决定量程的不确定度，增益误差决定读数的不确定度。元器件贡献的绝对误差可以在系统级进行校准，而与温度和时间相关的误差则难以校准。

24小时准确度主要由元器件的温度相关误差决定，通常规定为±（读数的百分比+量程的百分比）或±（读数的ppm+量程的ppm）。

失调误差

失调误差造成的不确定性与信号无关。例如，假设输入信号为0，最终的输出读数可能因放大器的失调漂移误差而有所不同。这意味着放大器的失调漂移误差会引起量程的不确定性。除了放大器的失调漂移之外，还需要考虑和分析电阻网络的温漂、ADC的零点漂移以及ADC的INL。（请注意，ADC INL被认为是失调不确定性，因为其非线性峰值未知）。

图1-2用于仿真LT5400-7的误差贡献：

• 理论上，当输入为0 V时，AFE电路的输出也应为0 V。
• 假设R8/R9和R1/R7之间的匹配度为1 ppm，则输出将为-0.5 μV，即-0.1 ppm误差。
• 假设R13/R12和R11/R10之间的匹配度为1 ppm，则输出将为-1.0 μV，即-0.2 ppm误差。
• LT5400-7的最大电阻匹配比温漂为±1 ppm/°C，因此其失调误差贡献为±0.2 ppm/°C。

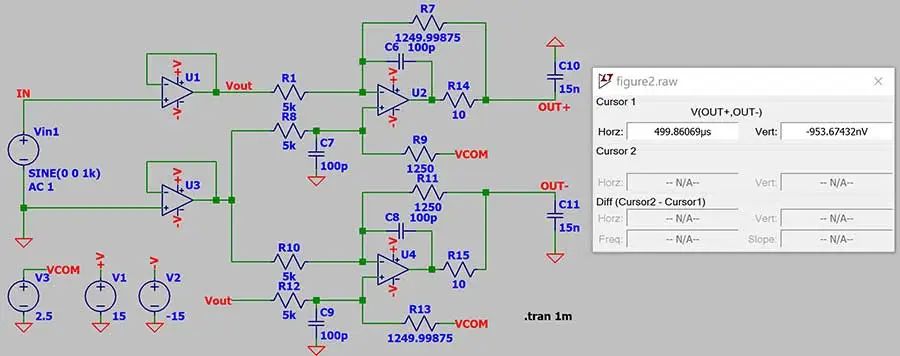
图1-2. 仿真LT5400-7匹配温漂带来的失调误差

表1-7总结了不同误差源带来的失调误差。

• 总温漂误差 = √0.0022 + 0.0052 + 0.22 + 0.0072 ≈ 0.2 ppm/°C.
• 考虑到温度不确定度为±1°C，故总温漂误差为0.2 ppm。
• 加上0.9 ppm ADC INL误差，总失调误差 = √0.22 + 0.92 ≈ 1 ppm.

表1-7. 失调误差源分析

增益误差

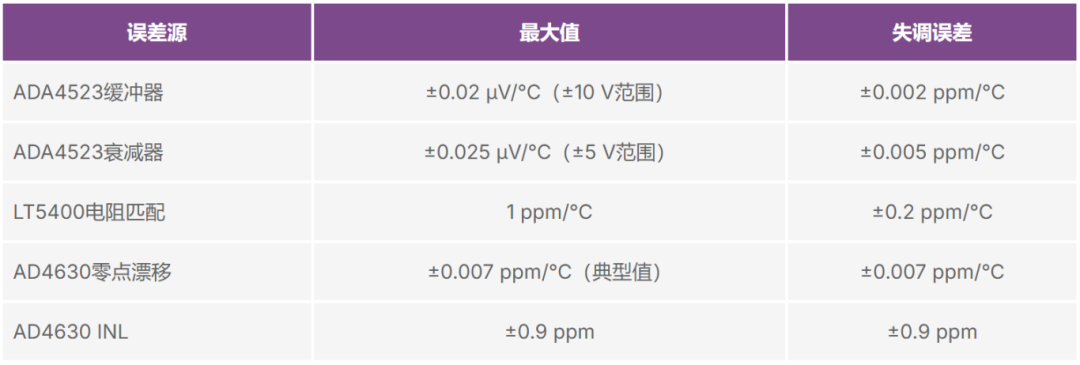
增益误差造成的不确定性与信号大小有关。例如，假设输入信号为0，最终输出读数可能不会因基准电压源失调漂移误差而有所不同。这意味着基准电压源的失调漂移误差会引起读数的不确定性。除了基准电压源的失调漂移之外，还需要考虑和分析电阻网络的温漂、ADC的增益误差漂移、基准电压源的滞回误差以及放大器的CMRR。

图1-3用于仿真LT5400-7贡献的增益误差：

• 理论上，当输入为10 V时，AFE电路的输出(OUT+OUT-)应为-5 V。
• 假设R8/R9与R1/R7之间的匹配度为1 ppm，R13/R12与R11/R10之间的 匹配度为1 ppm，则输出为–3.5 µV，若扣除–1 μV失调误差，则增益误差为–2.5 μV。
• LT5400-7的最大电阻匹配比温漂为±1 ppm/°C，因此增益误差贡献为±0.5 ppm/°C。

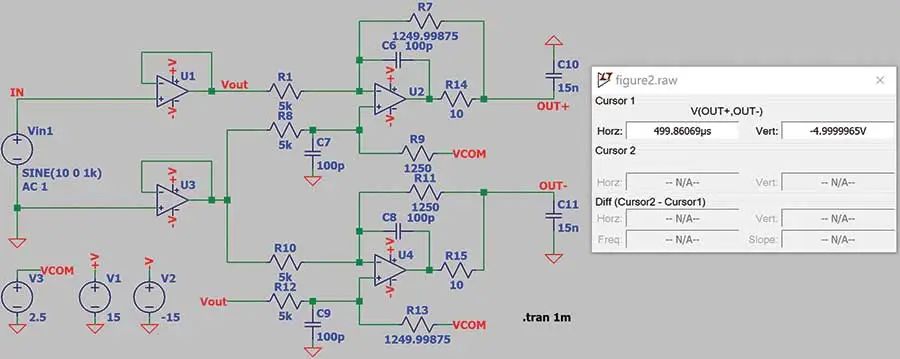
图1-3. 仿真LT5400-7匹配温漂带来的增益误差

ADA4523-1的CMRR最小值为140 dB，在±10 V输入下，缓冲器的Vcm变 化为±10 V，U4的Vcm变化为0 V至～4 V，有限的CMRR可能会随着输入变化而引起额外的增益误差。

温度变化为±1°C，因此可以忽略基准电压源的温度滞回误差。在工作温度范围较宽的其他应用中，需要考虑基准电压源滞回误差。

表1-8总结了不同误差源带来的增益误差。

• 总温漂误差 = √0.52 + 0.22 + 0.072 ≈ 0.54 ppm/°C.
• 考虑到温度不确定度为±1°C，故总温漂误差为0.54 ppm。
• 加上放大器CMRR误差和基准电压源温度滞回误差，总增益误 差 = √0.542 + 0.12 + 0.12 ≈ 0.6 ppm.

表1-8. 增益误差源及分析

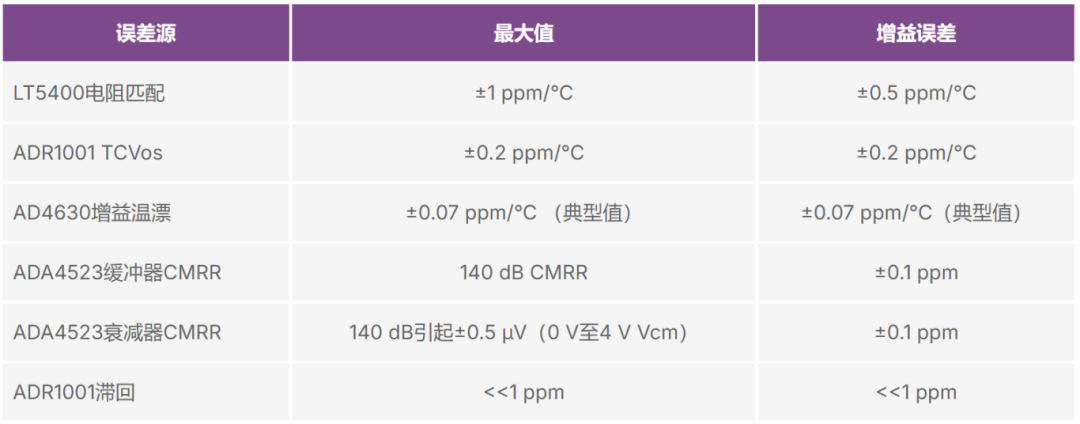
根据分析，对于由ADA4523-1 + LT5400-7 + AD4630-24 + ADR1001组成的 信号链，估计24小时准确度 (Ta = 23 ± 1°C) 为 ±(0.6 ppm + 1.0 ppm)。从表1-7和表1-8可以得出如下结论：放大器的温漂、基准电压源的温漂、电阻匹配温漂和ADC INL对于整个系统的准确度都很重要。

1年准确度(Ta = 23 ± 5°C)

对于仪表来说，准确度会随着时间的推移而降低。这是因为元器件参数会随时间而变化，不确定性会按照时间的平方根增加。仪表准确度与时间的指标非常重要。通常将其规定为±（读数的百分比+量程的的百分比）或±（读数的ppm+量程的ppm），时间可以为30天、90天、1年，工作环境温度为23 ± 5°C。

温度引起的失调误差和增益误差

参考表1-7，

• 总温漂误差 = √0.0022 + 0.0052 + 0.22 + 0.0072 ≈ 0.2 ppm/°C.
• 考虑到温度不确定度为±5°C，故总温漂误差为1 ppm。
• 加上0.9 ppm ADC INL误差，总失调误差 = √12 + 0.92 ≈ 1.35 ppm.

参考表1-8，

• 总温漂误差 = √0.52 + 0.22 + 0.072 ≈ 0.54 ppm/°C.
• 考虑到温度不确定度为±5°C，故总温漂误差为2.7 ppm。
• 加上放大器CMRR误差和基准电压源温度滞回误差，总增益误 差 = √2.72 + 0.12 + 0.12 ≈ 2.70 ppm.

根据分析，对于由ADA4523-1 + LT5400-7 + AD4630-24 + ADR1001组成的 信号链，估计准确度(Ta = 23 ± 5°C)为± (2.70 ppm ± 1.35 ppm)。

失调误差和增益误差随时间的变化

不同元器件对时漂指标的测试条件不同。假设全年的工作温度为28°C，则可以使用Arrhenius方程推导出28°C下的加速因子。加速因子计算公式如下

E~ a~ a为0.68 eV；k ~ B~ 为玻尔兹曼常数8.62×10-5eV/K；T~ op~ 和 T~stress ~分别为工作温度和应力测试温度，单位为K。

以LT5400为例，数据手册显示2000小时、35°C下，其电阻匹配比的时漂指标参数为< 2 ppm，可使用式1来计算其1年在28°C下的漂移值。加速因子：

这意味着28°C时，2000×1.81 = 3629小时的漂移指标参数为< 2 ppm，那么 1年（8760小时）后，LT5400可能会漂移 √8760/3629 × 2 ppm = 3.1 ppm。

同理，ADR1001在1000小时、25°C下的时漂指标参数为4 ppm，1年后 ADR1001可能会漂移13 ppm。ADR1399在1000小时、25°C下的时漂指标参数为7 ppm，1年后ADR1399可能会漂移23 ppm。

ADA4523-1的平均时漂<0.03 μV。

表1-9显示，28°C时1年后的估计准确度为± (13.1 ppm + 0.62 ppm)。

综合温度带来的不确定性± (2.70 ppm + 1.35 ppm) (Ta = 23 ± 5°C)，最终 1年准确度为：± (13.4 ppm + 1.5 ppm)。

表1-9. 1年后误差分析

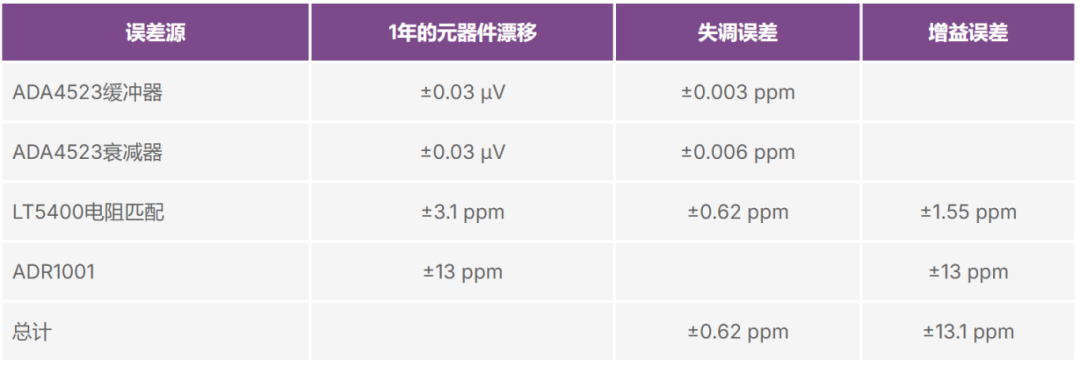
表1-10总结了ADA4523-1 + LT5400-7 + AD4630-24 + ADR1001的理论准确度指标参数，与市场上的典型七位半DMM的指标参数相近。

表1-10. 比较典型DMM与本解决方案的指标参数

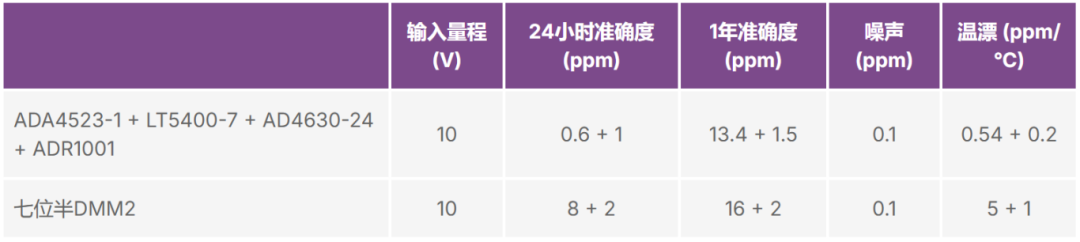
我们的理论分析和计算说明，利用0.1 ppm INL 2 MSPS SAR ADC AD4630、全集成超低温漂ADR1001、低噪声零漂移ADA4523-1和1 ppm/°C LT5400等器件构建的信号链可以实现出色的准确度性能。