请问一下关于Matlab要学习哪些知识呢

1.指数 对数 开方：exp log sqrt

• 
  
  

(1)字符串拼接：str = [str1,str2]
(2)字符串读取：str(3) %第三个字符 str(5:10) %第5到10的字符
(3)字符串变ASCLL：a = abs(str)
(4)ASCLL变字符串：char(a)
(5)字符串的执行：将字符串作为一个表达式来实现，直接在命令窗口输入函数
>> for n = 3:5eval(['M',num2str(n),'= magic(n)']) %eval函数用于将括号内的字符串视为语句并运行end (6)字符串的比较
比较两个字符串是否相等：strcmp(str1,str2)
比较两个字符串某一个字符是否相等：strncmp(str1,str2,9) %第9个是否相等
>> str1 = 'this is a matlab language'str1 =    'this is a matlab language'>> str2 = 'this is not the matlab language'str2 =    'this is not the matlab language'>> strcmp(str1,str2)ans =  logical   0>> strcmp(str1,str2,5)错误使用 strcmp输入参数太多。 >> strncmp(str1,str2,5)ans =  logical   1>> strncmp(str1,str2,9)ans =  logical   0 大小比较：str1 >= str2 若为真，全为0
>> str1 = 'matlab'str1 =    'matlab'>> str2 = 'MATLAB'str2 =    'MATLAB'>> str1 >= str2ans =  1×6 logical 数组   1   1   1   1   1   1 (7)寻找字符：strfind(str,‘a’) %字符串中a的位置是哪些，会标出位置
>> str = 'this is the matlab language'str =    'this is the matlab language'>> strfind(str,'a')ans =    14    17    21    25 3.多项式的生成
（1）直接输入法
>> p = [2 3 4 5 6 0 7]p =     2     3     4     5     6     0     7>> poly2sym(p) ans = 2*x^6 + 3*x^5 + 4*x^4 + 5*x^3 + 6*x^2 + 7 （2）特征值多项式输入法
>> a = [1 2 3 4 ;5 6 7 8; 9 8 7 6; 5 4 3 2]a =     1     2     3     4     5     6     7     8     9     8     7     6     5     4     3     2>> poly(a)  %特征多项式的系数ans =    1.0000  -16.0000  -80.0000    0.0000   -0.0000>> poly2sym(poly(a))  %系数数组转换为符号多项式 ans = x^4 - 16*x^3 - 80*x^2 + (499577829638779*x)/39614081257132168796771975168 - 5489766622375285/89202980794122492566142873090593446023921664  （3）由多项式的根逆推多项式
>> root=[-4 -2+2i -2-2i 5]root =  -4.0000 + 0.0000i  -2.0000 + 2.0000i  -2.0000 - 2.0000i   5.0000 + 0.0000i>> p = poly(root)  %poly函数是用于求以向量为解的方程或方阵的特征多项式,可以直接传递多项式方程的系数矩阵进行使用p =     1     3   -16   -88  -160>> diap(poly2sym(p))未定义函数或变量 'diap'。 是不是想输入:>> disp(poly2sym(p))x^4 + 3*x^3 - 16*x^2 - 88*x - 160 4.多项式求值
polyvalm:对矩阵的计算求值
polyval：对数组的计算求值
>> p = [1 -20 -16 480 98]  %多项式系数p =     1   -20   -16   480    98>> x = 4   %未知数x的值x =     4>> polyval(p,x)  %带入得到函数值ans =   738 5.求解多项式的根（求解多项式为0的值）：利用roots（p） %系数按降序
6.多项式的四则运算
（1）加
>> a = [8 2 2 8]a =     8     2     2     8>> b = [6 1 6 1]b =     6     1     6     1>> a + bans =    14     3     8     9>> y1 = poly2stm(a)未定义函数或变量 'poly2stm'。 是不是想输入:>> y1 = poly2sym(a) y1 = 8*x^3 + 2*x^2 + 2*x + 8 >> y2 = poly3sym(b)未定义函数或变量 'poly3sym'。 是不是想输入:>> y2 = poly2sym(b) y2 = 6*x^3 + x^2 + 6*x + 1 >> poly3sym(a + b)未定义函数或变量 'poly3sym'。 是不是想输入:>> poly2sym(a + b) ans = 14*x^3 + 3*x^2 + 8*x + 9 （2）乘
>> v1 = [1 2 3]v1 =     1     2     3>> v2 = [2 3 4]v2 =     2     3     4>> y1 = poly2sym(v1) y1 = x^2 + 2*x + 3 >> y2 = poly2sym(v2) y2 = 2*x^2 + 3*x + 4 >> v = conv(v1,v2)  %两个向量相乘的值v =     2     7    16    17    12>> Y = poly2sym(v) Y = 2*x^4 + 7*x^3 + 16*x^2 + 17*x + 12  (3)除 deconv ,和乘法相似
7.符号表达式的化简
（1）collect函数化简
>> syms x>> f = (x - 1)*(x - 2)*(x - 3) f = (x - 1)*(x - 2)*(x - 3) >> collect(f) ans = x^3 - 6*x^2 + 11*x - 6
（2）expand函数展开
>> syms x y z>> f1 = (x+y)^3 f1 = (x + y)^3 >> expand(f1) ans = x^3 + 3*x^2*y + 3*x*y^2 + y^3>> f2 =( x +y + z)^3 f2 = (x + y + z)^3 >> expand(f2) ans = x^3 + 3*x^2*y + 3*x^2*z + 3*x*y^2 + 6*x*y*z + 3*x*z^2 + y^3 + 3*y^2*z + 3*y*z^2 + z^3>> h1 = cos(x - y) h1 = cos(x - y) >> expand(h1) ans = cos(x)*cos(y) + sin(x)*sin(y)
（3）horner函数：嵌套式
>> f = x^3 -6 * x^2+11*x f = x^3 - 6*x^2 + 11*x >> horner(f) ans = x*(x*(x - 6) + 11)
（4）factor函数：实现多项式的因式分解
>> syms x y>> factor(x^3 - y^3) ans = [ x - y, x^2 + x*y + y^2] 8.符号与数值之间的转换：digits函数与vpa函数
9.复合函数的运算：compose函数
>> syms x y z t u>> f = 1/(1+x^2) f = 1/(x^2 + 1) >> g = sin(y) g = sin(y) >> h = x^t h = x^t >> p = exp(-y/u) p = exp(-y/u) >> compose(f,g) ans = 1/(sin(y)^2 + 1) >> compose(f,g,t) ans = 1/(sin(t)^2 + 1)
10.反函数的运算：finverse函数
>> syms x y   %定义一些符号变量,用来进行符号运算用的>> f = x^2 + y f = x^2 + y >> finverse(f,y) ans = - x^2 + y >> finverse(f) ans = (x - y)^(1/2)
11.表达式的微分和求导
>> syms x>> diff(x^3+3*x^2+2*x +5)  %对表达式求导 ans = 3*x^2 + 6*x + 2 >> diff(sin(x^3),6)   %对表达式求6阶导 ans = 7290*x^9*cos(x^3) - 9720*x^3*cos(x^3) - 360*sin(x^3) + 17820*x^6*sin(x^3) - 729*x^12*sin(x^3) >> syms x y>> diff(x*y + y^2 +sin(x) + cos(y),y)   %对表达式求y的偏导 ans = x + 2*y - sin(y)>> diff(x*y + y^2 +sin(x) + cos(y),x)  %对x求导 ans = y + cos(x) >> diff(x*y + y^2 +sin(x) + cos(y),y,3)  %对y求3阶导 ans = sin(y)
12.符号表达式的极限
>> syms h n x>> result = limit((sin(x + h) - sin(x))/h,h,0)  %求极限 result = cos(x) >> limit(sin(x)/x,x,0)   %求极限 ans = 1 >> limit(sin(x)/x,x,0,'right')  %求右极限 ans = 1 >> limit(sin(x)/x,x,0,'left')  %求左极限 ans = 1
13.符号表达式的积分：利用int函数
>> int(-2 *x/(1 + x^2)^2) %不定积分 ans = 1/(x^2 + 1) >> syms l z>> int (besselj(l,z),0,l) %besselj函数是避免溢出和精度损失，范围在0~1 ans = (1/2^l*l^(l + 1)*hypergeom(l/2 + 1/2, [l/2 + 3/2, l + 1], -l^2/4))/gamma(l + 2) >> syms x k>> f = exp(-(k * x)^2) f = exp(-k^2*x^2) >> int(f,-inf,inf)  %定积分 ans = piecewise(k^2 < 0, (Inf*1i)/(sign(k)^2)^(1/2), k ~= 0 & angle(k^2) in Dom::Interval([-pi/2], [pi/2]) | 0 <= real(k^2), pi^(1/2)/(k^2)^(1/2), ~k^2 < 0 & real(k^2) < 0 & ~angle(k^2) in Dom::Interval([-pi/2], [pi/2]), int(exp(-x^2*k^2), x, -Inf, Inf))
14.符号表达式的级数求和：symsum函数
symsum(fun,var,a,b):其中fun是通项表bai达式，var为求和变量，a为求和起点，b为求和终点
>> syms x k>> s1 = symsum(1/k^2,1,inf) s1 = pi^2/6 >> s2 = symsum(x^k,k,0,inf) s2 = piecewise(1 <= x, Inf, abs(x) < 1, -1/(x - 1))
15.泰勒级数：taylor函数
>> syms x>> f = 1/(2+cos(x)) f = 1/(cos(x) + 2) >> r = taylor(f,8) 16.Fourier变换
(1)直接通过调用fourier和ifourier命令来实现函数的正变换和反变换
>> syms t w>> ft = Heaviside(t)找不到 'Heaviside' 的完全匹配项(区分大小写)。最接近的匹配项为: heaviside(在 D:matlabmulutoolboxsymbolicsymbolicheaviside.m 中) 是不是想输入:>> ft = heaviside(t)  %heaviside( )表示的就是阶跃函数啊，阶跃函数定义就是当x>0时，值为1；x<0时，值为0 ft = heaviside(t) >> Fw = fourier(ft) Fw = pi*dirac(w) - 1i/w >> ft = ifourier(Fw) ft = (pi + pi*sign(x))/(2*pi) (2)根据Fourier变换的定义，利用积分指令int来实现上述功能
17.Laplace变换(拉普拉斯变换)
>> syms s t w x y>> ilaplace(1/(s - 1)) ans = exp(t) >> ilaplace(1/(t^2 + 1)) ans = sin(x)
18.常微分方程求解
19.matlab绘图基础
[tr]函数名功能描述[/tr]

plot	在X轴和Y轴上都按线性比例绘制二维函数图形
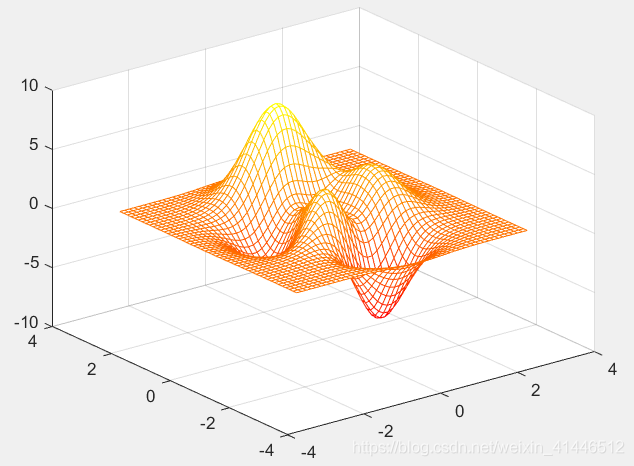
plot3	在X轴，Y轴和Z轴上都按线性比例绘制三维函数图形
loglog	在X轴和Y轴上都按对数比例绘制二维函数图形
semilogx	在x轴按对数比例，在y轴上按线性比例绘制二维函数图形
semilogy	在y轴按对数比例，在x轴上按线性比例绘制二维函数图形
plotty	绘制双y轴函数图形

• 
  
  

(1)二维线性颜色及线形
>> x = 0:0.01*pi:2*pi;>> y1 = sin(x);>> y2 = sin(x-0.25*pi);>> y3 = sin(x-0.5*pi);>> plot(x,y1,y2,y3)>> plot(x,y1,x,y2,x,y3)>> >> plot(x,y1,'-,b',x,y2,'--,r',x,y3,'-,gh')错误使用 plotcolor/linetype 参数出错。 >> plot(x,y1,'-.b',x,y2,'--r',x,y3,'-.gh')
（2）分段函数绘制（注意：绘制一个图形后，不要把图形窗口叉掉，不然下一个图形仍不会有此次绘制的图形）
hold on:保持图形
>> x = 0:0.1:1;>> y = x;>> plot(x,y)>> hold on>> x = 1:0.1:2;>> y = 0.5*x.^4+0.5;>> plot(x,y)>> hold on>> x = 2:0.1:5;>> y = -x.^2+9*x-5.5;>> plot(x,y)
21.三维图形处理
网格的命令
>> [x,y] = meshgrid(-2:0.1:2,-2:0.1:2);>> z = x.*exp(-x.*2-y.^2);>> plot3(x,y,z)>> >> [x,y,z] = peaks(30);>> mesh(x,y,z);
22.surf函数（三维色图）
>> [x,y] = meshgrid([-4:0.5:4]);>> z = sqrt(x.^2 + y.^2);>> surf(z)
23.瀑布流水型
>> [x,y,z] = peaks(30);>> waterfall(z)
24.特殊的三维图形
（1）柱状图
>> y = [5 2 1; 3 1 4;1 5 9; 5 5 5; 4 3 2];>> yy =     5     2     1     3     1     4     1     5     9     5     5     5     4     3     2>> bar3(y)  %3表示三维>> cylinder  %立体三维柱状图 高，直径均为1>> t = 0:pi/10:2*pi;>> [x,y,z] = cylinder(2+cos(t));>> surf(x,y,z) （2）绘制球体
>> [m,n,p] = sphere(50);  %球体半径>> t = abs(p);>> surf(m,n,p,t)
（3）饼图
>> x = [2,4,6,8];>> pie3(x,[0,0,1,0])
（4）柱状图转为直角坐标里面的图
>> theta = 0:pi/20:2*pi;>> rho = sin(theta);>> [t,r] = meshgrid(theta,rho);  %生成绘制3D图形所需的网格数据>> z = r.*t;>> [x,y,z] = pol2cart(t,r,z);>> mesh(x,y,z)
（5）球体转为直角坐标里面的图
>> theta = 0:pi/20:2*pi;>> rho = sin(theta);>> [t,r] = meshgrid(theta,rho);>> z = r.*t;>> [x,y,z] = sph2cart(t,r,z);>> mesh(x,y,z) 25.坐标轴标签及注释
>> x = 0:0.1*pi:2*pi;>> y = sin(x);>> plot(x,y)>> xlabel('x(0-2*pi)','fontweight','bold');>> ylabel('f = sin(x)','fontweight','bold')>> text(pi,sin(pi),'leftarrowsin(t) = 0','fontsize',16)>> text(5*pi/4,sin(5*pi/4),'leftarrowsin(t) = -0.707','fontsize',16)




26.图例标注（不同曲线代表含义）
>> x = pi:pi/20:pi;>> plot(x,cos(x),'-ro',x,sin(x),'-.b')>> plot(x,cos(x),'-ro',x,sin(x),'-.b')>> h = legend('cos','sin',2)
27.改变坐标轴控制更好观察曲线
>> x = 0:0.025*pi:pi/2;>> plot(x,tan(x),'-ro')>> axis([0 pi/2 0 5])   %x的范围在0——pi/2    y在0——5
28.对数据进行截取（点击图形任意一点，列出其横纵坐标）：利用ginput函数
>> x = 0:0.025:2*pi;>> y = sin(x);>> plot(x,y)>> [m,n] = ginput(1)   %是数字1
29.图形图像的色彩控制
（1）colormap函数
>> [x,y,z] = peaks;>> mesh(x,y,z)  %mesh()用于绘制不是特别精细的三维曲面网格图,同一层面的线条用相同的颜色表示>> colormap(autumn(128))




（2）brighten函数
>> brighten(-0.9)>> brighten(0.9)









(3)colorbar函数:为峰值函数图形添加色标
>> surf(peaks(30))   %surf是绘制三维曲面>> colorbar    >> caxis([-2,2])    %改变色标范围为[-2,2]




(4) flat faceted interp的差别
>> subplot(3,1,1)   %将多个图画到一个平面上的工具>> sphere(16)>> axis square    %将图形改为方形>>> shading flat




>> subplot(3,1,2)>> sphere(16)>> axis square>> shading faceted




>> subplot(3,1,3)>> sphere(16)>> axis square>> shading interp




在一个窗口展现





30.改变图形的视角
>> x = 0:0.1:2*pi;>> z = sin(x);>> y = zeros(size(x));>> colordef white>> subplot(2,2,1)>> plot3(x,y,z)>> grid;>> view(-37.5,30)>> subplot(2,2,2)>> plot3(x,y,z)>> grid;>> view(-37.5+90,30)>> subplot(2,2,3)>> plot3(x,y,z)>> grid;>> view(0,90)




31.光源的改变
>> h = surf(peaks);>> light('Position',[1 0 0 1]);错误使用 light值必须为包含 3 个元素的数值向量 >> light('Position',[1 0 0]); 32.执行函数
[tr]执行函数名称功能描述[/tr]

assignin	在MATLAB工作区间中分配变量
builtin	外部加在调用内置函数
eval	字符串调用函数
evalc	执行MATLAB的表达式
evalim	计算工作区间中的表达式
feval	字符串调用M文件
run	运行脚本文件

33.Simulink对图形化模型的仿真
（1）模型的编译阶段
（2）连接阶段
（3）仿真阶段
34.ployfit函数：进行曲线拟合
35.矩形积分：cumsum函数
梯形积分：trapz函数
一元函数积分：quad函数
二元积分：dblquad函数
三元积分：triplequad函数
36.复数的生成
>> re = rand(3,2)re =    0.8147    0.9134    0.9058    0.6324    0.1270    0.0975>> im = rand(3,2)im =    0.2785    0.9649    0.5469    0.1576    0.9575    0.9706>> com = re + i * imcom =   0.8147 + 0.2785i   0.9134 + 0.9649i   0.9058 + 0.5469i   0.6324 + 0.1576i   0.1270 + 0.9575i   0.0975 + 0.9706i
37.求实部、虚部、共轭复数
>> a = 1/(3 + 2i)    %一个复数式子a =   0.2308 - 0.1538i>> real(a)   %求实部ans =    0.2308>> imag(a)   %求虚部ans =   -0.1538>> conj(a)    %求共轭复数ans =   0.2308 + 0.1538i
38.打开图像
>> a = imread('aaa','jpg');>> imshow(a); 修改尺寸
>> x1 = imresize(a,2,'nearest')  %放大两倍>> imshow(x1) ‘nearest’ （默认值）最近邻插值
‘bilinear’ 双线性插值
‘bicubic’ 双三次插值