一、前言
之前在STM32F407上现实了直播声卡,实现的经典Schroeder混响模型和Moorer混响模型,得到不错效果。后来得知卷积混响最为真实地表现空间的特性,所以也就尝试在MCU上实现一个高精度的卷积混响(卷积点数为32768),目前MCU出来的混响效果算得上一流水准,本人也在计划在ADI的21489或者SC584上更高精度的卷积混响。
二、卷积方式
1、conv1是使用MATLAB自带卷积函数conv
2、conv2和conv3是改进后卷积过程,具有减少运算量特点,方便嵌入式移植
clear;
%get reverb ir
[rir,fs] = audioread(“inputs/Room 3.wav”);
rir = mean(rir, 2);
%set ir num
ir_num = 30000;
%plot ir data
rir = rir(1:ir_num,1);
rir_y = zeros(1, ir_num);
for n = 1:1:ir_num
rir_y(n) = n/fs;
end
rir_y = rir_y‘;
figure(1);
plot(rir_y,rir);
title(’Reverb IR‘);
xlabel(’time(s)‘);
% LOAD ANECHOIC SOUND
[input,Fs] = audioread(’inputs/TEST MONO GUITAR 48kHZ 24bits 4S.wav‘);
%conv 1
ir_conv1 = rir;
y_conv1 = conv(input,ir_conv1);
y_conv1_w = y_conv1 / max(abs(y_conv1));
audiowrite(’outputs/ir_conv1-reverb.wav‘, y_conv1_w, fs)
%conv 2
y_conv2 = my_conv2(input,rir);
y_dirr = (y_conv1 - y_conv2);
figure(2);
plot(y_dirr);
title(’conv1 and conv2 error‘);
axis([0, length(y_dirr),-0.001, 0.001]);
y_conv2_w = y_conv2 / max(abs(y_conv2));
audiowrite(’outputs/ir_conv2-reverb.wav‘, y_conv2_w, fs)
%conv 3
y = my_conv3(input,rir,ir_num);
y_conv3 = y’;
y_conv3 = y_conv3(1:length(y_conv1),1);
y_dirr = (y_conv1 - y_conv3);
figure(3);
plot(y_dirr);
title(‘conv1 and conv3 error’);
axis([0, length(y_dirr),-0.001, 0.001]);
y_conv3_w = y_conv3 / max(abs(y_conv3));
audiowrite(‘outputs/ir_conv3-reverb.wav’, y_conv3_w, fs)
以下是仿真结果
figure1是使用ROOM的脉冲响应(IR)文件,长度大约在0.7S
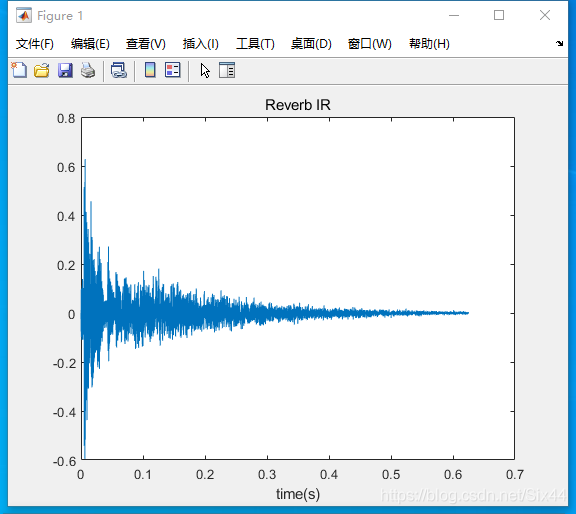
figure2是分别使用conv1和conv2卷积后的结果差值,可以看到两种方式差值基本为0

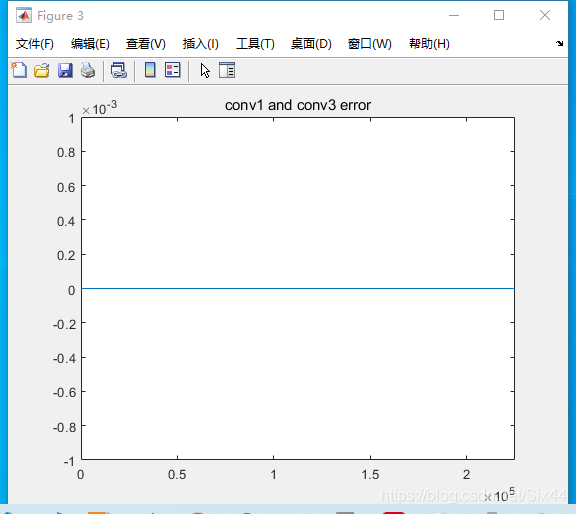
figure3是分别使用conv1和conv3卷积后的结果差值,可以看到两种方式差值基本为0
三、声音对比
一、前言
之前在STM32F407上现实了直播声卡,实现的经典Schroeder混响模型和Moorer混响模型,得到不错效果。后来得知卷积混响最为真实地表现空间的特性,所以也就尝试在MCU上实现一个高精度的卷积混响(卷积点数为32768),目前MCU出来的混响效果算得上一流水准,本人也在计划在ADI的21489或者SC584上更高精度的卷积混响。
二、卷积方式
1、conv1是使用MATLAB自带卷积函数conv
2、conv2和conv3是改进后卷积过程,具有减少运算量特点,方便嵌入式移植
clear;
%get reverb ir
[rir,fs] = audioread(“inputs/Room 3.wav”);
rir = mean(rir, 2);
%set ir num
ir_num = 30000;
%plot ir data
rir = rir(1:ir_num,1);
rir_y = zeros(1, ir_num);
for n = 1:1:ir_num
rir_y(n) = n/fs;
end
rir_y = rir_y‘;
figure(1);
plot(rir_y,rir);
title(’Reverb IR‘);
xlabel(’time(s)‘);
% LOAD ANECHOIC SOUND
[input,Fs] = audioread(’inputs/TEST MONO GUITAR 48kHZ 24bits 4S.wav‘);
%conv 1
ir_conv1 = rir;
y_conv1 = conv(input,ir_conv1);
y_conv1_w = y_conv1 / max(abs(y_conv1));
audiowrite(’outputs/ir_conv1-reverb.wav‘, y_conv1_w, fs)
%conv 2
y_conv2 = my_conv2(input,rir);
y_dirr = (y_conv1 - y_conv2);
figure(2);
plot(y_dirr);
title(’conv1 and conv2 error‘);
axis([0, length(y_dirr),-0.001, 0.001]);
y_conv2_w = y_conv2 / max(abs(y_conv2));
audiowrite(’outputs/ir_conv2-reverb.wav‘, y_conv2_w, fs)
%conv 3
y = my_conv3(input,rir,ir_num);
y_conv3 = y’;
y_conv3 = y_conv3(1:length(y_conv1),1);
y_dirr = (y_conv1 - y_conv3);
figure(3);
plot(y_dirr);
title(‘conv1 and conv3 error’);
axis([0, length(y_dirr),-0.001, 0.001]);
y_conv3_w = y_conv3 / max(abs(y_conv3));
audiowrite(‘outputs/ir_conv3-reverb.wav’, y_conv3_w, fs)
以下是仿真结果
figure1是使用ROOM的脉冲响应(IR)文件,长度大约在0.7S

figure2是分别使用conv1和conv2卷积后的结果差值,可以看到两种方式差值基本为0

figure3是分别使用conv1和conv3卷积后的结果差值,可以看到两种方式差值基本为0

三、声音对比

 举报
举报





 举报
举报

