传感器使用前要进行标定, 标定时必定需要进行曲线拟合。若用计算机处理很简单, 但实际中用微控制器中标定时, 只能进行一般的代数运算,无矩阵运算, 处理就显得非常不方便。最小二乘法推导了二次多项式曲线拟合待定系数的代数计算公式, 应用这些公式来处理数据非常方便。
设有一组实测数据(x i , yi)i =1 , 2 , … , n , 其拟合函数为

一、MATLAB中验证
假定一种传感器的标准输入与输出曲线如图1(红色曲线)所示,由于环境以及外部干扰原因导致传感器输入与输出曲线发生偏移,如图1(蓝色曲线)。如果要得到传感器正确的数据就需要一条矫正曲线,将输入带有误差的曲线矫正成红色的标准曲线。首先我们要先确认误差曲线,如图2所示。红色为平滑后的曲线。
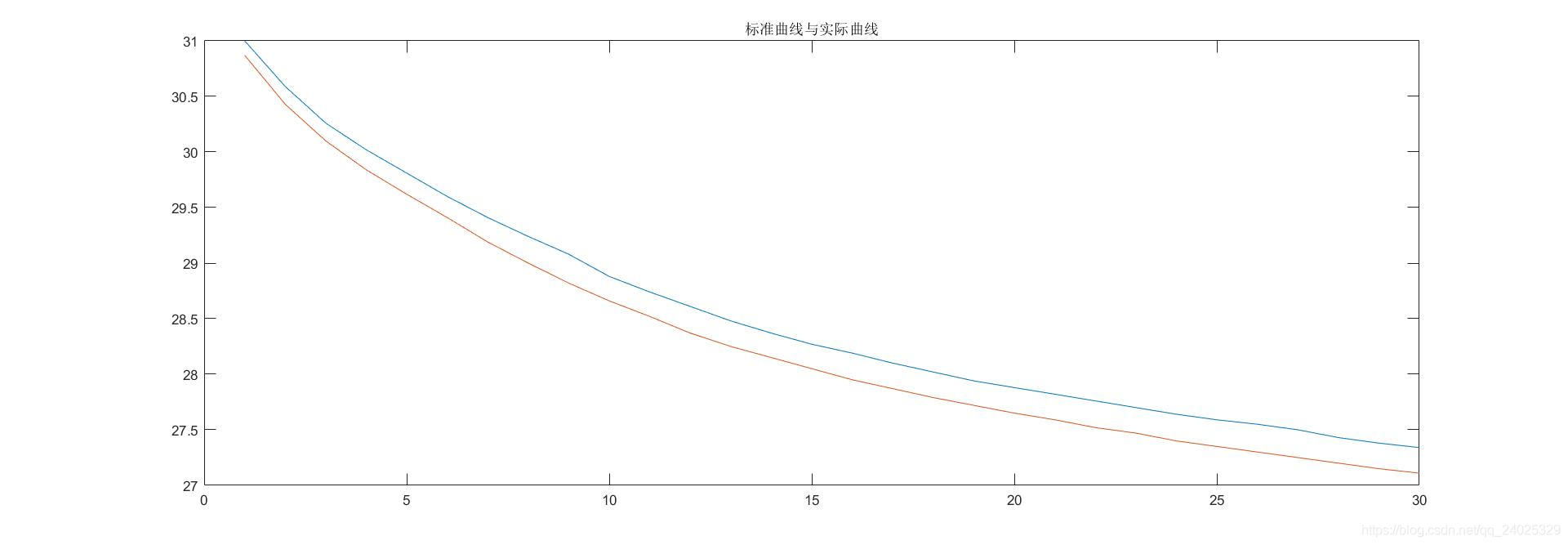
图1:标准曲线与实际曲线
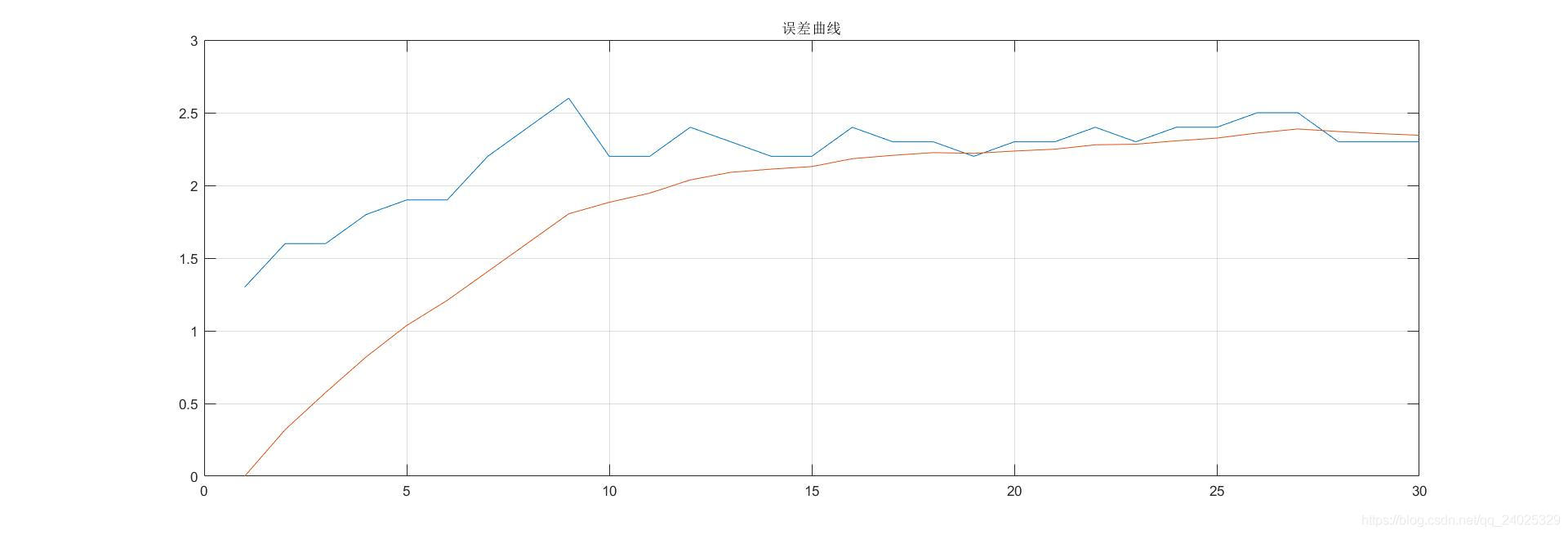
图2:误差曲线
MATLAB矫正过程简述如下:
将标准曲线导入MATLAB
将现场采集到的误差曲线导入MATLAB
取标准曲线和带有误差的曲线个7个数据
计算误差(拟合曲线的输出)
利用最小二乘法集合误差曲线
F(标准输出) = F(现场输入)-F(误差)
拟合后的曲线如图3所示:
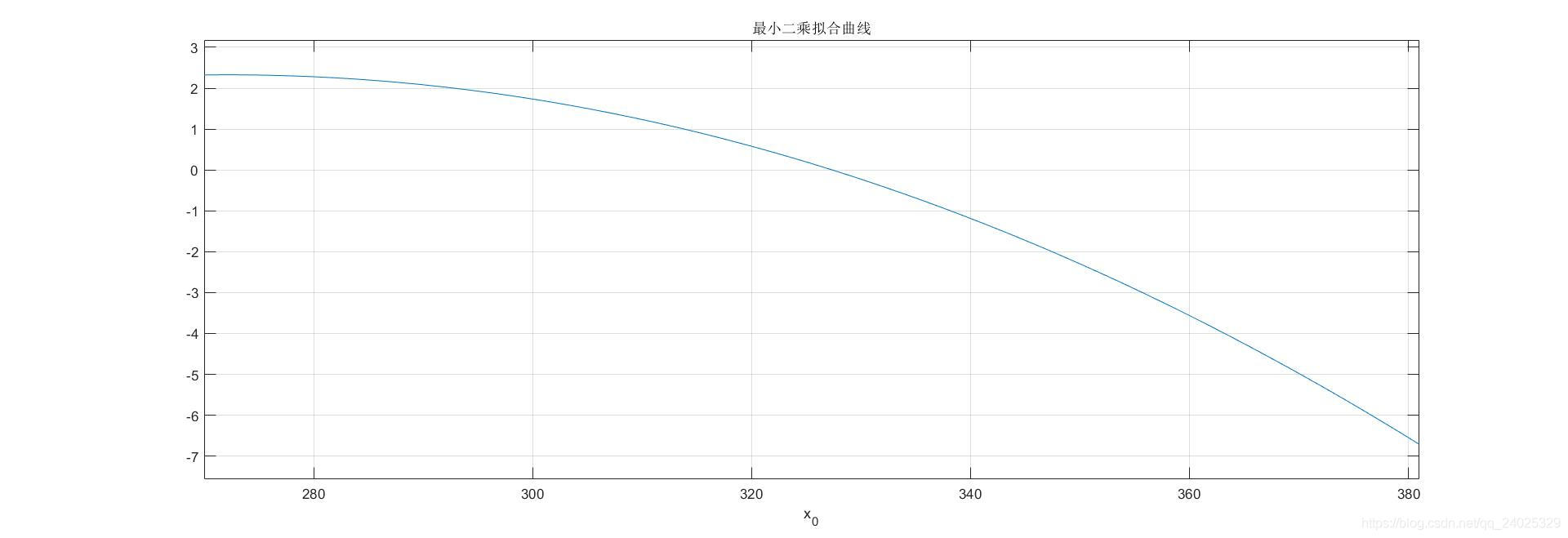
拟合曲线
MATLAB代码如下(可直接运行):
%==============定义标准====================%
a = [310.0 305.9 302.6 300.2 298.1 296.0 294.1 292.4 290.8 288.8 287.4 286.1 284.8 283.7 282.7 281.9 281.0 280.2 279.4 278.8 278.2 277.6 277.0 276.4 275.9 275.5 275.0 274.3 273.8 273.4];
a = a/10.0;
%==============定义实际输入====================%
b = [308.7 304.3 301.0 298.4 296.2 294.1 291.9 290.0 288.2 286.6 285.2 283.7 282.5 281.5 280.5 279.5 278.7 277.9 277.2 276.5 275.9 275.2 274.7 274.0 273.5 273.0 272.5 272.0 271.5 271.1];
b = b/10.0;
bb = [b(1),b(5),b(10),b(15),b(20),b(25),b(30)];%需要拟合的数据,取输入的其中7个数据
%=============定义标准输出(为误差)=================%
out = [a(1)-b(1),a(5)-b(5),a(10)-b(10),a(15)-b(15),a(20)-b(20),a(25)-b(25),a(30)-b(30)];
%=================一下为计算参数===================%
b1 = sum(bb);
b2 = sum(bb.^2);
b3 = sum(bb.^3);
b4 = sum(bb.^4);
c1 = sum(out);
c2 = sum(out.*bb);
c3 = sum(out.*bb.^2);
n=7;%拟合数据长度为 7
k = n*b2*b4 + 2*b1*b2*b3 - n*b3^2 - b1^2*b4 - b2^3;%%计算K
a0 = ((b2*b4-b3^2)*c1 + (b2*b3-b1*b4)*c2 + (b1*b3-b2^2)*c3 )/k;
a1 = ((b2*b3-b1*b4)*c1 + (n*b4-b2^2)*c2 + (b1*b2-n*b3)*c3 )/k;
a2 = ((b1*b3-b2^2)*c1 + (b1*b2-n*b3)*c2 + (n*b2-b1^2)*c3 )/k;
%%拟合函数%%%%%
syms funb x0
funb = a0 + a1*x0 + a2*x0*x0;%%函数
%================误差曲线和平滑后的曲线============%
error = a-b;%得出数据误差
t = 1:1:30;%定义横坐标
error_p = zeros(1,30);%定义空向量
for i=2:30
error_p(i) = error_p(i-1)*0.8 + error(i)*(1-0.8);%一阶低通滤波
end
plot(t,error);%画误差曲线
hold on;
plot(t,error_p);%画平滑误差曲线
figure;
ezplot(funb,[27,38]);%画出拟合曲线
二、在STM32中实现
自STM32F4系列推出之后,STM32已经带有DSP运算单元了,即使需要实时的曲线拟合,STM32也可以完全的胜任了。
计算代码如下:
/*
显示函数
误差曲线拟合
其中 n 为需要拟合数据长度
其中g_dData 为待拟合的曲线数据(x)
其中g_dOut 为拟合曲线的输出(Y)
*/
void disposeHMI()
{
double b1=0;
double b2=0;
double b3=0;
double b4=0;
double c1=0;
double c2=0;
double c3=0;
double n=0;
double k=0;
unsigned char i;
unsigned int j;
if(g_cUartData == 0xfe)//如果下发测量指令
{
g_cUartData = 0;//清空
Bi = 0;
delay_ms(200);
Bi = 1;
//=============================一下为拟合==========================//
//=========================拟合数据为 1 5 10 15 20 25 30 ====7个数======//
{
n=7;
//================一下计算BCk系数
for(i=0;i《7;i++)
{
b1 += g_dData[i];
}
for(i=0;i《7;i++)
{
b2 += pow(g_dData[i],2);
}
for(i=0;i《7;i++)
{
b3 += pow(g_dData[i],3);
}
for(i=0;i《7;i++)
{
b4 += pow(g_dData[i],4);
}
for(i=0;i《7;i++)
{
c1 += g_dOut[i];
}
for(i=0;i《7;i++)
{
c2 += g_dOut[i]*g_dData[i];
}
for(i=0;i《7;i++)
{
c3 += g_dOut[i]*pow(g_dData,2);
}
k = n*b2*b4 + 2*b1*b2*b3 - n*b3*b3 - b1*b1*b4 - b2*b2*b2;
//==============一下为计算系数============================//
a0 = ((b2*b4-b3*b3)*c1 + (b2*b3-b1*b4)*c2 + (b1*b3-b2*b2)*c3 )/k;
a1 = ((b2*b3-b1*b4)*c1 + (n*b4-b2*b2)*c2 + (b1*b2-n*b3)*c3 )/k;
a2 = ((b1*b3-b2*b2)*c1 + (b1*b2-n*b3)*c2 + (n*b2-b1*b1)*c3 )/k;
}
}
}
三、总结
利用本文推导的二次项式曲线拟合待定系数的代数计算公式求待定系数比较方便, 然后, 再进行曲线拟合, 其拟合准确度也很高, 尤其用单片机进行标定时优点更为显著。笔者能力有限,如有错误望提示更正。
传感器使用前要进行标定, 标定时必定需要进行曲线拟合。若用计算机处理很简单, 但实际中用微控制器中标定时, 只能进行一般的代数运算,无矩阵运算, 处理就显得非常不方便。最小二乘法推导了二次多项式曲线拟合待定系数的代数计算公式, 应用这些公式来处理数据非常方便。
设有一组实测数据(x i , yi)i =1 , 2 , … , n , 其拟合函数为

一、MATLAB中验证
假定一种传感器的标准输入与输出曲线如图1(红色曲线)所示,由于环境以及外部干扰原因导致传感器输入与输出曲线发生偏移,如图1(蓝色曲线)。如果要得到传感器正确的数据就需要一条矫正曲线,将输入带有误差的曲线矫正成红色的标准曲线。首先我们要先确认误差曲线,如图2所示。红色为平滑后的曲线。

图1:标准曲线与实际曲线

图2:误差曲线
MATLAB矫正过程简述如下:
将标准曲线导入MATLAB
将现场采集到的误差曲线导入MATLAB
取标准曲线和带有误差的曲线个7个数据
计算误差(拟合曲线的输出)
利用最小二乘法集合误差曲线
F(标准输出) = F(现场输入)-F(误差)
拟合后的曲线如图3所示:

拟合曲线
MATLAB代码如下(可直接运行):
%==============定义标准====================%
a = [310.0 305.9 302.6 300.2 298.1 296.0 294.1 292.4 290.8 288.8 287.4 286.1 284.8 283.7 282.7 281.9 281.0 280.2 279.4 278.8 278.2 277.6 277.0 276.4 275.9 275.5 275.0 274.3 273.8 273.4];
a = a/10.0;
%==============定义实际输入====================%
b = [308.7 304.3 301.0 298.4 296.2 294.1 291.9 290.0 288.2 286.6 285.2 283.7 282.5 281.5 280.5 279.5 278.7 277.9 277.2 276.5 275.9 275.2 274.7 274.0 273.5 273.0 272.5 272.0 271.5 271.1];
b = b/10.0;
bb = [b(1),b(5),b(10),b(15),b(20),b(25),b(30)];%需要拟合的数据,取输入的其中7个数据
%=============定义标准输出(为误差)=================%
out = [a(1)-b(1),a(5)-b(5),a(10)-b(10),a(15)-b(15),a(20)-b(20),a(25)-b(25),a(30)-b(30)];
%=================一下为计算参数===================%
b1 = sum(bb);
b2 = sum(bb.^2);
b3 = sum(bb.^3);
b4 = sum(bb.^4);
c1 = sum(out);
c2 = sum(out.*bb);
c3 = sum(out.*bb.^2);
n=7;%拟合数据长度为 7
k = n*b2*b4 + 2*b1*b2*b3 - n*b3^2 - b1^2*b4 - b2^3;%%计算K
a0 = ((b2*b4-b3^2)*c1 + (b2*b3-b1*b4)*c2 + (b1*b3-b2^2)*c3 )/k;
a1 = ((b2*b3-b1*b4)*c1 + (n*b4-b2^2)*c2 + (b1*b2-n*b3)*c3 )/k;
a2 = ((b1*b3-b2^2)*c1 + (b1*b2-n*b3)*c2 + (n*b2-b1^2)*c3 )/k;
%%拟合函数%%%%%
syms funb x0
funb = a0 + a1*x0 + a2*x0*x0;%%函数
%================误差曲线和平滑后的曲线============%
error = a-b;%得出数据误差
t = 1:1:30;%定义横坐标
error_p = zeros(1,30);%定义空向量
for i=2:30
error_p(i) = error_p(i-1)*0.8 + error(i)*(1-0.8);%一阶低通滤波
end
plot(t,error);%画误差曲线
hold on;
plot(t,error_p);%画平滑误差曲线
figure;
ezplot(funb,[27,38]);%画出拟合曲线
二、在STM32中实现
自STM32F4系列推出之后,STM32已经带有DSP运算单元了,即使需要实时的曲线拟合,STM32也可以完全的胜任了。
计算代码如下:
/*
显示函数
误差曲线拟合
其中 n 为需要拟合数据长度
其中g_dData 为待拟合的曲线数据(x)
其中g_dOut 为拟合曲线的输出(Y)
*/
void disposeHMI()
{
double b1=0;
double b2=0;
double b3=0;
double b4=0;
double c1=0;
double c2=0;
double c3=0;
double n=0;
double k=0;
unsigned char i;
unsigned int j;
if(g_cUartData == 0xfe)//如果下发测量指令
{
g_cUartData = 0;//清空
Bi = 0;
delay_ms(200);
Bi = 1;
//=============================一下为拟合==========================//
//=========================拟合数据为 1 5 10 15 20 25 30 ====7个数======//
{
n=7;
//================一下计算BCk系数
for(i=0;i《7;i++)
{
b1 += g_dData[i];
}
for(i=0;i《7;i++)
{
b2 += pow(g_dData[i],2);
}
for(i=0;i《7;i++)
{
b3 += pow(g_dData[i],3);
}
for(i=0;i《7;i++)
{
b4 += pow(g_dData[i],4);
}
for(i=0;i《7;i++)
{
c1 += g_dOut[i];
}
for(i=0;i《7;i++)
{
c2 += g_dOut[i]*g_dData[i];
}
for(i=0;i《7;i++)
{
c3 += g_dOut[i]*pow(g_dData,2);
}
k = n*b2*b4 + 2*b1*b2*b3 - n*b3*b3 - b1*b1*b4 - b2*b2*b2;
//==============一下为计算系数============================//
a0 = ((b2*b4-b3*b3)*c1 + (b2*b3-b1*b4)*c2 + (b1*b3-b2*b2)*c3 )/k;
a1 = ((b2*b3-b1*b4)*c1 + (n*b4-b2*b2)*c2 + (b1*b2-n*b3)*c3 )/k;
a2 = ((b1*b3-b2*b2)*c1 + (b1*b2-n*b3)*c2 + (n*b2-b1*b1)*c3 )/k;
}
}
}
三、总结
利用本文推导的二次项式曲线拟合待定系数的代数计算公式求待定系数比较方便, 然后, 再进行曲线拟合, 其拟合准确度也很高, 尤其用单片机进行标定时优点更为显著。笔者能力有限,如有错误望提示更正。

 举报
举报





 举报
举报

