很多童鞋学编程、学通讯都不清楚硬件底层时如何传输数据的,刚好最近整理了些概念和原理,方便大家参阅。如有不妥,欢迎指正!
模拟信号与数字信号
“模拟信号”(analog signal)是“模拟数据”的电平信号表示形式,其信号电平是一个随时间连续变化的(中间没有跳跃)函数曲线(每个周期的曲线是一样的)
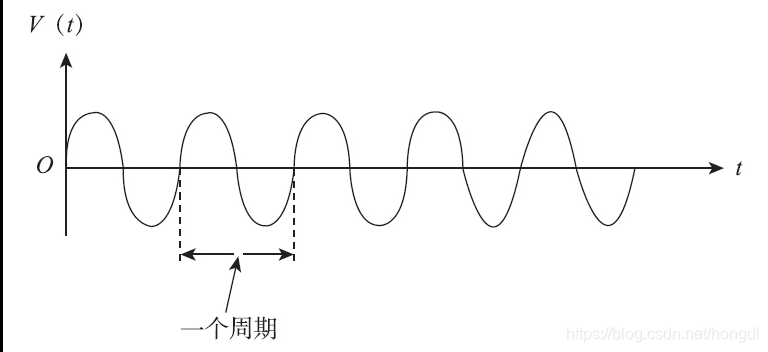
而“数字信号”(digital signal)是“数字数据”的信号电平表示形式(由一个个“码元”组成,一个“码元”就包括一个脉冲周期),用两种不同的电平表示二进制的0和1信号所对应的电压脉冲,是离散(非连续变化)的。
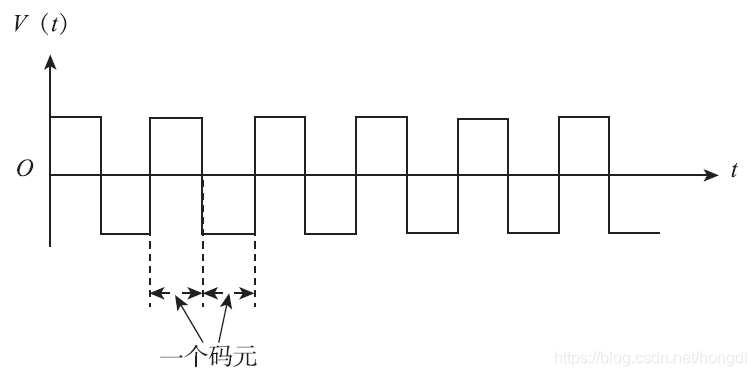
基带、频带与宽带
信源信号(也就是信号源发送的信号)经过信源编码之后成为离散的二进制数字信号。我们用一些离散的波形来代替这些数字信号。这些离散的信号可以直接进行传输,或者调制到载波上进行传输。这样就形成了两种最基本的数字信号的传输类型——基带传输和频带传输。在频带传输基础上,通过信道的复用又诞生了一种称为宽带传输的数据传输类型。
基带是指信源发出的,没有经过调制(进行频谱搬移和变换)的原始电信号所固有的频带(频率带宽),也称为基本频带。
而频带是指对基带信号调制后所占用的频率带宽(一个信号所占有的从最高的频率到最低的频率之差)。
所谓“宽带”(Broadband)就是采用比音频(4kHz)更宽的频带,该频带包括了大部分电磁波频谱,是相对前面的“频带”来说的,因为“频带”只具有有限的频率宽度。使用这种宽频带进行的数据传输就称为宽带传输。宽带传输其实与频带传输具有相同的特点,它也需要对信源发出的原始信号进行调制,但它将一个信道分成多个子信道,分别传送音频、视频和数字信号,而且宽带传输中的所有子信道都可以同时发送信号。
基带信号与频带信号
信源发出的没有经过调制的原始电信号(原汁原味)就称为基带信号。基带信号的特点是频率较低,信号频谱是从零频率的直流成分开始的。如果一个信号包含了频率达到无穷大的交流成分和可能的直流成分,则这个信号就是基带信号。
经过调制后的基带信号称为频带信号。频带信号的频率被限制在一个特定的频带中。如果一个信号只包含了一种频率的交流成分,或者有限几种频率的交流成分,我们就称这种信号为频带信号。
根据原始电信号的特征,基带(或频带)信号可分为数字基带(或频带)信号和模拟基带(或频带)信号(相应的,信源也分为数字信源和模拟信源),具体由其信源类型确定。数字基带信号往往包含丰富的低频分量,甚至直流分量。在某些具有低通特性的有线信道中,特别是传输距离不太远的情况下,数字基带信号可以直接传输。
在基带传输中,由于不调制,所以整个信道只传输一种信号,通信信道利用率低。在基带传输中,需要在信源端对数字信号进行编码,在信宿端对编码的数据进行解码恢复,这分别是由编码器和解码器完成的。由于在近距离传输范围内基带信号的衰减不大,从而信号内容不会发生变化。因此在传输距离较近时,计算机网络都采用基带传输类型。大多数的局域网使用基带传输,如以太网、令牌环网等。
而频带传输广泛应用于广域网中,因为在这种网络通信中,往往需要同时发送多种信号(如数据信号、路由信号,以及各种网络控制信号),这时就可以利用高频率的信号来调制低频率信号,以实现同步传输,也提高了信道利用率。由于频带传输中所用的传输频率通常比较高,所以也适用于远距离的广域网通信
“串行传输”和“并行传输”
计算机网络数据通信的数据传输方式可分“串行传输”和“并行传输”两种。
“串行传输”指的是数据流以串行方式一位位地在一条信道上传输。

很显然,串行传输只需要一条传输信道(当然在一个接口中可以有多条这样的串行传输信道),传输速度比较慢,但易于实现、费用低,是目前主要采用的一种传输方式。另外,串行传输存在一个收、发双方如何保持码组或者说字符同步(也就是如果识别一个字符包括哪几个比特位)的问题。这个问题不解决,接收方就不能从接收到的数据流中正确地区分出一个个字符来,因而传输将失去意义。如何解决码组或字符同步的问题,就涉及异步传输方式和同步传输方式了。
采用串行传输方式的典型代表有计算机串行接口(简称串口,对应RS-232C标准),还有如USB接口、SATA(串行ATA)磁盘接口等,
“并行传输”指的是数据以一组或者整个字符的方式在多条并行信道上同时传输。
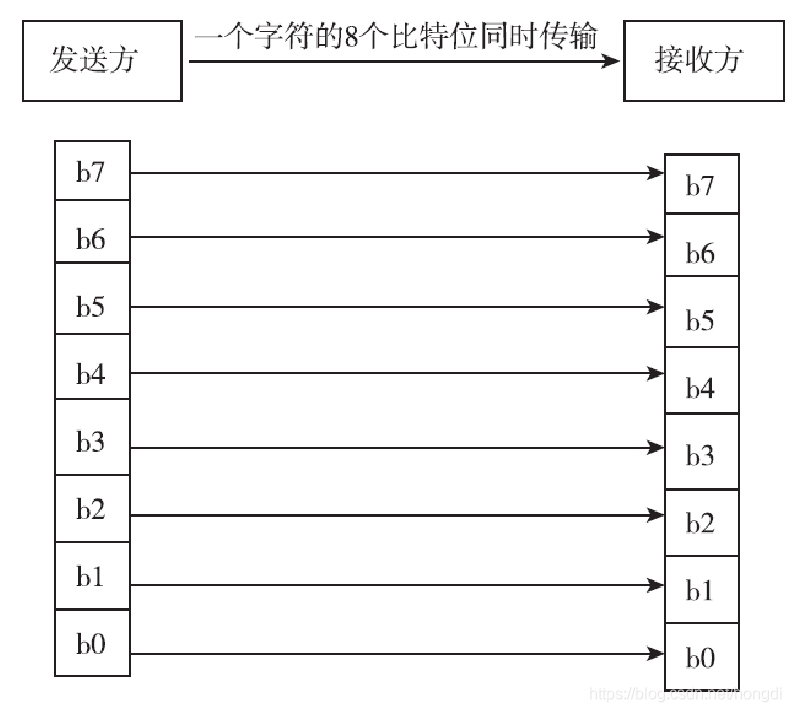
采用并行传输方式的典型代表有计算机上连接打印机的并口、磁盘ATA(或者IDE)接口等,计算机主板上CPU与其他芯片的数据传输也是采用并行传输方式。
同步传输与异步传输
串行传输接收端存在一个如何从串行数据比特流中正确地划分出发送的一个个字符的问题,也就是字符同步的问题。在串行数据通信中同步问题十分关键。发送端一位一位地把信息通过介质发往接收端,接收端必须识别信息的开始和结束,而且必须知道每一位的持续时间。只有这样,接收端才能从传输线路上正确地取出被传送的数据。根据实现字符同步的方式不同,有同步传输(Synchronous Transmission)和异步传输(Asynchronous Transmission)两种方式。
同步就是指通信双方在传输过程中是同步进行的(也就是接收端与发送端同时开始工作,并且接收端按数据的发送顺序进行接收),同步的依据就是双方有相同的时钟参考,能同时开始数据的发送和接收。通常这个时钟参考是同步时钟线或同一个时钟源。
同步传输是一种以数据块为传输单位(通常是以“帧”为单位的),以相同的时钟参考进行数据传输的模式,因此又称为区块传输。在该传输模式下,每一比特数据的持续传输时间都是相等的,而且在每个字符的传输过程中,两个字符间传输所需等待的时间也是相同的。
另外,在同步传输中的数据块的开始和结尾部分都有一个用于数据帧同步的特殊字符、特定的字节或特定的帧,这具体要视所采用的同步方法而定。同步传输分为面向字符的同步传输、面向比特的同步传输和面向字节的同步传输等几种。

采用同步传输的技术代表有SDH(Synchronous Digital Hierarchy,同步数字系列)、STM(Synchronous Transfer Module,同步传输模块)和HDLC(High level Data Link Control,高级数据链路控制)等。
与下面将要介绍的“异步传输”方式比较,“同步传输”在技术上较复杂,但不需要对每个字符加单独的“起始”和“停止”比特,接收方不必对每个字符进行开始和停止的操作,只需要在检测到帧同步字符时接收它们即可。而且同步传输是以帧为传输单位(异步传输是以字符为传输单位的,一个帧通常有500字节,4000比特)进行传输的,只需在一个数据帧的前后加上标志字符即可,因此传输效率高,常用于较高速的数据传输。
异步传输是指通信双方没有相同的时钟参考(也就是发送端和接收端不同时开始工作),但双方在数据传输速率上是同步的。即指每个字符之间是异步的,但一个字符内的每一位还是同步的。
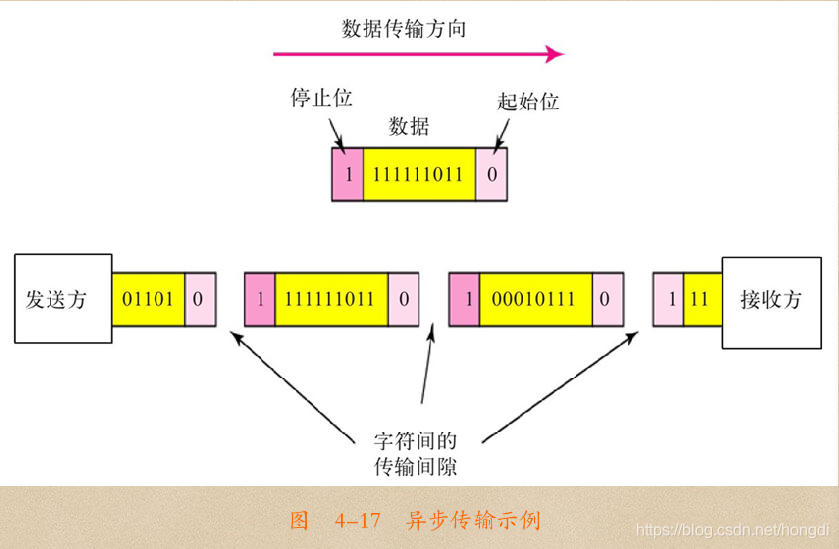
异步传输是以字符为单位进行数据传输的。在发送每一字符代码的前面均加上一个“起始位”信号(长度为1比特,极性为0),用以标记一个字符的开始;在一个字符代码的最后加上一个“停止位”信号(长度为1或2比特,极性为1),用以标记一个字符的结束。字符位占5~8位,具体取决于数据所采用的字符集,如电报码字符为5位,ASCII码字符为7位。
异步传输的典型代表就是ATM(异步传输模式)技术,目前仍是城域网和广域网中主流的交换技术之一。早期还有一种B-ISDN(宽带ISDN)技术,也是异步传输技术的代表。
在“异步传输”中,发送方可以在任何时刻发送这些比特组,而接收方从不知道它们会在什么时候到达,故不需要同时开始接收。被发送的比特组需进行排除等候。最典型的一个异步传输实例就是我们访问互联网上的网站,点击一个网站,网站服务器一般不会马上响应,而是等它有资源响应时才响应,所以网站打开时往往有些延时。
异步传输的优点是字符同步实现简单,收发双方的时钟信号不需要严格同步。缺点是对每一字符都需加入“起、止”码元,使传输效率降低。例如假设每次传送7比特的信息,每个字符需要另外加一个起始位和一个停止位。另外,异步通信主要处理ASCII编码的信息,这意味着增加了第3个控制位,即奇偶校验位,这样每个字符附加3位控制位,传输效率只有70%。
比特率与波特率
比特率通常又称信息传输速率,是指单位时间内传输的二进制代码的有效位(bit)数,用Rb(注意这里是小写的b)表示。比特率是用来描述可直接在计算机网络数字线路上传输的数字数据的传输速率,常用的单位有bit/s(b/s或bps,每秒比特数)、kbit/s(kb/s或kbps,每秒千比特数)或Mbit/s(Mb/s或Mbps,每秒兆比特数)。但要注意,此处的k和M分别为1000和1 000 000,而不是涉及计算机存储器容量时的1024和1048576。
波特率(Baud rate)是指一个数字信号在被调制后,数字信号对载波的调制速率,也即单位时间内载波参数(如频率、相位等)变化的次数,单位为B。如果是非调制的二进制数字信号,波特率与比特率数值上是相等的,所以波特率通常是针对经过调制后的数字信号传输速率。
波特率的单位为Baud,用RB(注意这里是大写的B)表示。一个数字脉冲,或者直接说是一个二进制位称为一个码元,波特率也可以理解为在单位时间内传输的码元数。这里的码元可以是二进制的,也可以是多进制的。如二进制的字母A的ASCII码是01000001,可用7个脉冲来表示(最高位为校验位,不计入码元中),所以A可认为是由7个码元组成的。若1s内传2400个码元,则波特率为2400B。
对于数字数据,比特率与波特率的关系与数据所采用的进制有关。因为每个码元或符号通常都含有一定比特数的信息量,所以比特率(Rb)与波特率(RB)有如下关系:
Rb=RB×log2M(b/s)
式中的M为符号的进制数,如二进制、八进制、十六进制。例如码元速率为1200B,采用八进制(M=8)时,则可计算出对应的信息速率Rb=1200×log28=3600(b/s);如果采用的是二进制(M=2),则信息速率为Rb=1200×log22=1200(b/s),可见,二进制的波特率和比特率在数值上是相等的。
在采用了数字调制技术的数字通信中,比特率与波特率的关系还与所采用的调制技术有关。
两相调制(单个调制状态对应1个二进制位)的比特率的数值等于波特率的数值;四相调制(单个调制状态对应2个二进制位)的比特率的数值为波特率的数值的2倍;八相调制(单个调制状态对应3个二进制位)的比特率的数值为波特率的数值的3倍;依此类推。
“带宽”是指信道中每秒传输的最大信息量,也就是一个信道的最大数据传输速率,单位也是“位/秒”(b/s或bps)。带宽是一种理想状态(不受任何干扰,没有任何衰减)下的信道传输速率,而上面介绍的“数据传输速率”是指当前实际的数据传输速率,通常情况下“数据传输速率”永远小于或等于“带宽”值(事实上一般不可能等于带宽的,因为传输过程中不可能完全不受干扰,线路性能一般也不可能完全达到理想状态)。
数字信号不失真传输的最大传输速率限制
物理层的任何一个信道,它所能承受的信号频率(或者说是信道带宽)是有限的,就像任何一条河流只能承受一定峰值的水流量一样。在信道中,超出限定的频率范围的信号都将被直接滤出,不能通过信道,就像河流中任何超出它流速限制的水流量最终不能形成实际速率的水流量一样。
在计算数字信道中最大传输速率方面,有两个非常有名的准则或定理,那就是奈奎斯特准则(简称奈氏准则)和香农公式。
由于数字信号(这里特指没有被调制的原始数字信号,也就是上面所说的数字基带信号)的频带(这里是指信号的频率带宽)可以非常宽(从直流一直到无限高的频率),但其主要能量集中在低频段,而且数据通信中的电缆传输信道只允许比较低的频率成分通过理想低通信道,高频成分将被滤去,这就造成了输出波形的失真。失真的输出波形顶部变圆,底部变宽(称为波形拖尾),使得一个码元的波形展宽到其他码元位置,影响到其他码元,这种影响称为码间干扰。
理想“低通信道”是指只要信号频率不超过某个上限值都能够不失真地通过此信道;而频率超过该上限值的所有高频分量都不能通过该信道。与之相对的还有一种称为理想“带通矩形信道”,它是指仅允许在上下限之间的信号频率成分不失真地通过,其他频率成分不能通过。
要使信道中传输的数字信号不失真,信道中的数据传输速率必须限制在某个范围之内,这又与信道类型有关。1924年,美国著名物理学家奈奎斯特(Nyquist),经过多次实验证明,为了确保数字信号不失真传输,在理想低通信道(基带传输中的信道)下实际的最高码元传输速率(即无码间干扰的最高波特率)必须在下式计算结果之内:
最高码元传输速率(MaxRB)=2W
式中W是理想低通信道的带宽,单位为赫(Hz),MaxRB为最高码元传输速率,单位为Raud(波特)。这就是著名的奈奎斯特第一准则,其指出了在理想低通信道(也就是4.2.4节中介绍的基带传输中的信道)中,为了确保数字信号的不失真传输,信道带宽和最大码元传输速率之间的关系。
以上奈奎斯特第一准则描述了有限带宽、无噪声信道的最大数据传输速率与信道带宽的关系。美国的另一位著名物理学家——克劳德·香农(Claude Elwood Shannon)也在数据通信领域有权威的发现,那就是“香农公式”。这个公式描述了有限信道带宽、有随机热噪声信道(更接近真实环境)的最大传输速率与信道带宽、信噪比(信号平均功率与噪声功率之比)之间的关系。香农公式指出:在有随机热噪声的信道上传输数据信
号时,最大数据传输速率Rmax与信道带宽B、信噪比S/N的关系如下所示:
Rmax=B×log2(1+S/N)
式中Rmax的单位为bps,信道带宽B的单位为Hz,信噪比S/N通常用dB(分贝)表示,可用10×log10(S/N)公式来计算信噪比的分贝数。若已知S/N=1000,则根据公式可很快得出用分贝数表示的信噪比为30dB。如果再已知信道带宽B=3000Hz,则Rmax≈30kbps。它表示对于带宽只有3000Hz的通信信道,信噪比在30dB时,无论数据采用二进制或更多的离散电平值表示,都不能用越过30kbps的数据传输速率。
模拟信号不失真还原的最小采样频率限制
在计算机设备中只能接收数字信号,如果在信道中传输的是模拟信号(通过公共交换电话网络进行的远程网络连接的电话线路中传输的都是模拟信号),在接收端必须进行模/数转换,生成数字信号;同样如果将在一个计算机设备中的数字信号还原到某条模拟线路中进行传输,则又要进行数/模转换,还原成原来的模拟信号。这里最关键的是由模拟信号转换成数字信号,因为在这个转换过程中要确保数据不失真。
因为模拟信号是随时间连续变化的,而数字信号则是离散的,所以在模/数转换过程中,就需要离散地在模拟信号上抽取一定的信号样本,形成数字信号样本,以便可以不失真地代表原始数据本身,也使得抽取的数字信号样本在需要时能还原为原始的模拟信号。这就涉及一个“采样频率”(简单地说就是每隔多少时间提取一次信号波)的问题。
要确保信号不失真的恢复,最低的采样率需要达到多少呢?采样过程所应遵循的规律称为采样定理,又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。
只要这些采样点的时间间隔Δt≤1/2F,便可根据各采样值完全恢复原来的信号f(t)。简单地讲就是,在进行模拟/数字信号的转换过程中,当采样频率fs,max大于或等于信号中最高频率fmax的2倍时(fs,max≥2fmax),采样之后的数字信号就可完整地保留原始信号中的信息,原来的连续信号就可以从采样样本中完全重建出来,否则采
样信号后的频率将会混叠。一般实际应用中保证采样频率为信号最高频率的5~10倍。
由以上定理可以得知,如果已知信号的最高频率fH,就可以得出保证完全重建信号的最低采样频率是2fH。相反,如果已知采样频率,则可以得出保证信号完全重建所允许的最高信号频率。但要注意的是,这里有一个条件,那就是被采样的信号必须是带限的,也就是是有限带宽的,信号中高于某一给定频率的成分必须是0,或者至少非常接近0。只有这样,在重建信号时这些频率成分的影响才可以忽略不计。如果被采样的信号不是带限的,采样后信号的频率就会产生重叠,即高于采样频率一半的成分将被重建成低于采样频率一半的信号,最终导致信号不能被完全恢复。
数字基带信号编码
数字基带传输模式中传输的信号是要经过编码的原始数字信号。但数字基带信号的类型有很多,常见的有矩形脉冲、三角波、高斯脉冲和余弦脉冲等。其中最常用的是矩形脉冲,因为矩形脉冲易于形成和变换。
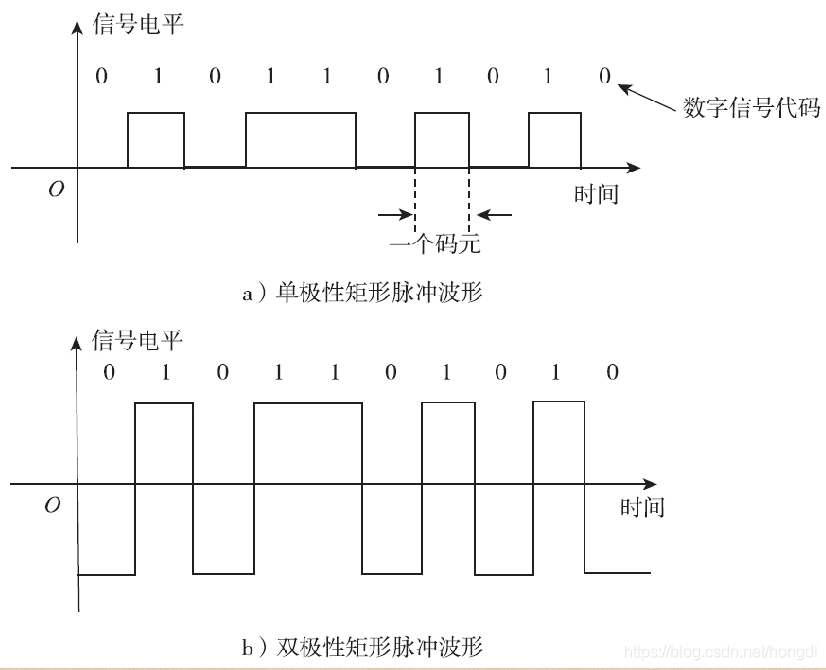
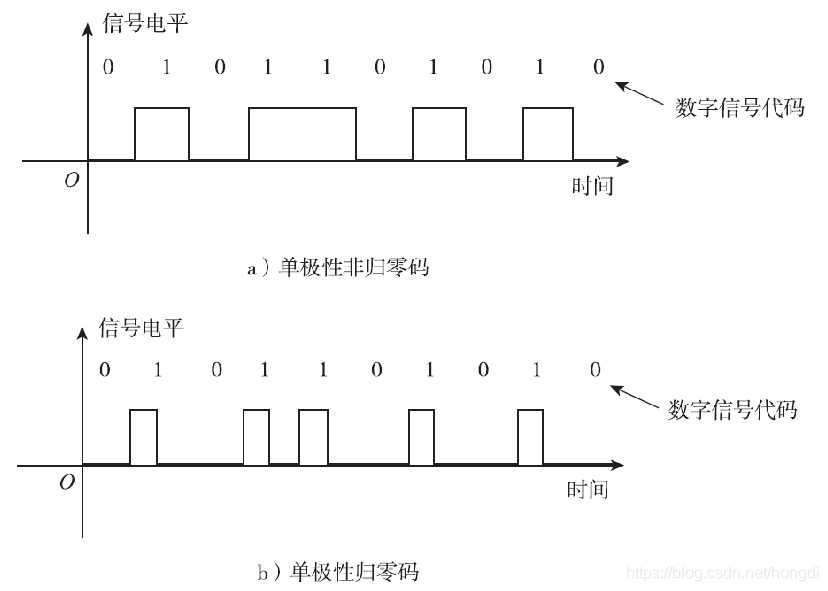
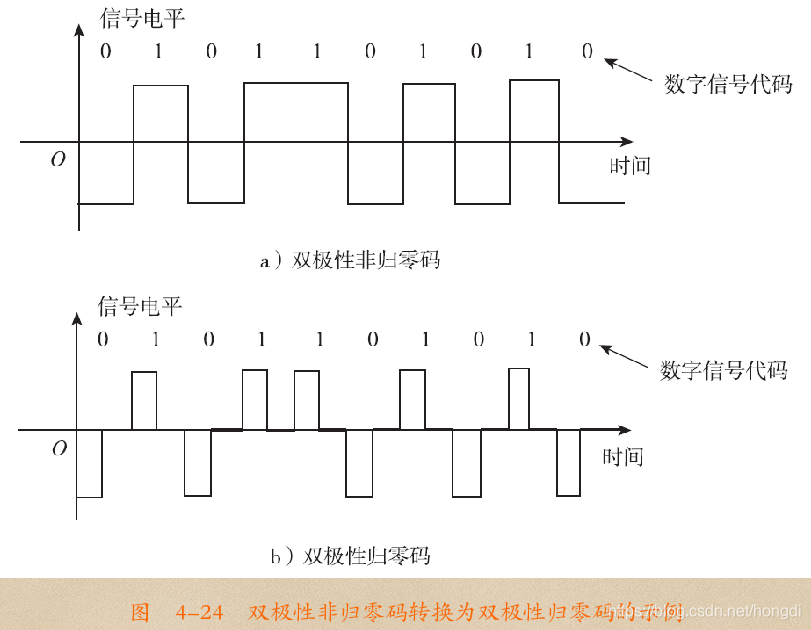
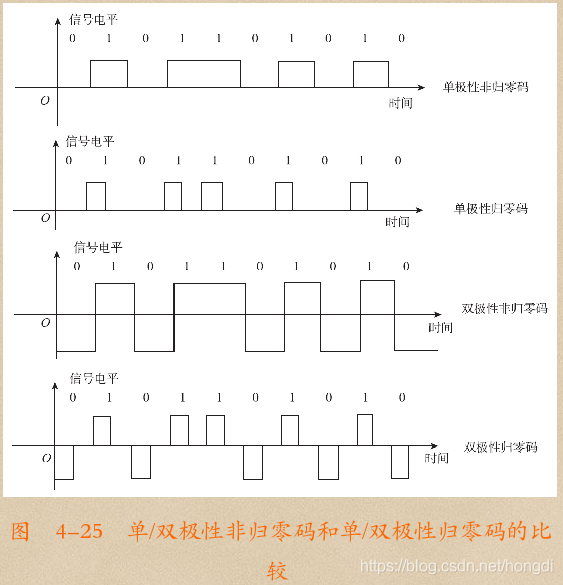
在矩形脉冲数字信号中主要有以下四种波形:单极性不归零波形、单极性归零波形、双极性不归零波形、双极性归零波形。

信道编码
在实际的基带传输系统中,并不是所有编码类型的电信号波形都能在信道中传输。例如上节介绍的含有直流分量和较丰富低频分量的单极性基带波形就不适宜在低频传输特性差的信道中传输,因为其功率较弱,在传输过程中有可能造成信号严重畸变。另外,当信息代码中包含有长串的连续“1”或“0”时,非归零波形呈现出连续的固定电平,会出现无法获取同步的问题。单极性归零码在传送连续“0”信息代码时也会存在同样的问题。因此,信息码在进行传输之前,必须经过码型变换,变换为适用于信道传输的码型,这就是通常所说的传输码,也称线路码或信道编码。
传输码型的选择原则:
一是要能从基带信号中提取定时信息(位同步脉冲信息),所以要求传输码型应含有(或者经变换后含有)时钟频率分量(不能出现0电平),且编码转换后不能出现过多的连续“0”码或“1”码,否则提取的时钟信号就会很不稳定,引起同步偏移;
二是要无直流分量、低频成分少,否则影响信号在信道中的传输;
三是信号中高频分量要尽量少,以节省传输频带并减少码间串扰。
常见的传输码型有:传号反转交替码(AMI码)、三阶高密度双极性码(HDB3码)、传号反转码(CMI码)、数字双相码(曼彻斯特码)和差分曼彻斯特码。
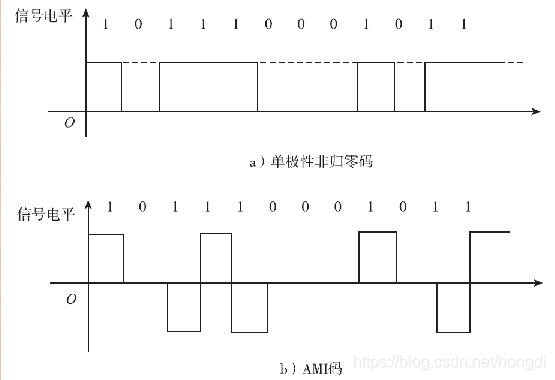
AMI码的优点是:由于“1”码元采用了正、负电平交替,所以AMI码的有信号部分的频谱中不含直流成分,高频和低频成分也很少。另外,AMI码的编译码电路简单,便于利用传号极性交替规律观察误码情况。鉴于这些优点,AMI码是CCITT建议采用的传输码型之一。
AMI码的不足是:当原二进制信号代码出现连续的“0”码时,信号电平会长时间不变,造成提取定时信号的困难(也就是同步比较困难),解决连续“0”码问题的有效方法之一是采用后面要介绍的HDB3码,它是AMI码的改进码型。
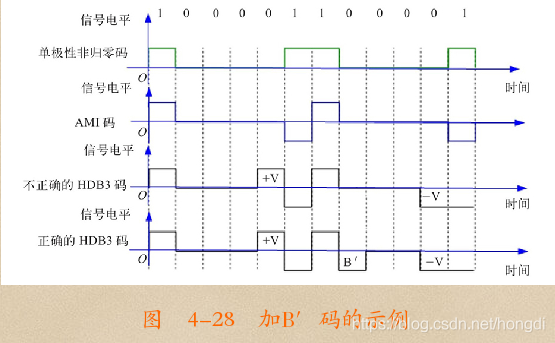
HDB3码除保持了前面介绍的AMI码的优点外,同时还将连续“0”码限制在3个以内,更有利于位定时信号的提取。HDB3码是应用最为广泛的码型,已成为CCITT协会推荐使用的基带传输码型之一。
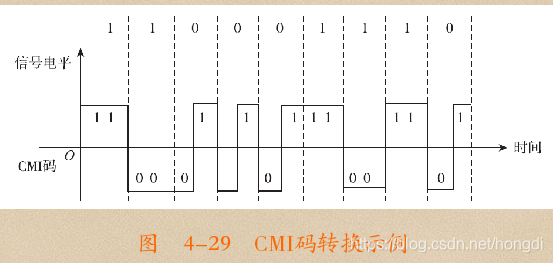
CMI码具有一定的检测错误的能力,因为“1”码交替地用“11”和“00”来表示,而“0”又固定用“01”表示,所以正常情况下,转换后的编码“10”是不可能在信道中出现的,连续的“00”或“11”也是不可能出现的,这样一来就可以用来检测因信道传输而产生的错误。但是CMI码不能纠错。CMI码也没有直流分量(没有零电平,只有正、页电平),且有频繁出现的波形跳变,便于恢复定时信号(也就是便于同步)。
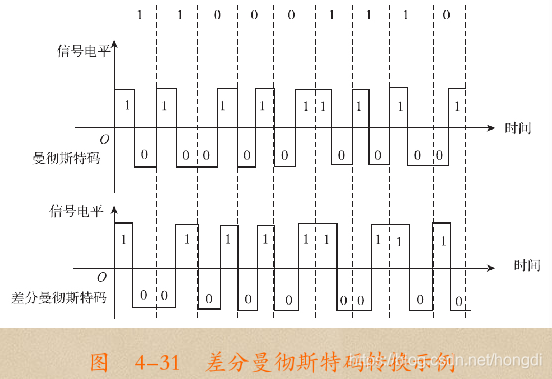
曼彻斯特码的优点也是无直流分量(全部转换为双极性电平,无零电平),最长连续“0”码或连续“l”码的个数仅为2,非常容易实现同步,编译码电路简单。因为如果原来基带信号是连续的“1”码,转换后都为“10”两个码了,不会出现连续的“1”码,如果原来基带信号是连续的“0”码,转换后都为“01”两个码了,不会出现连续的“1”码或“0”码。仅当原来基带信号是连续的“01”码时,才可能出现转换后的连续“0”码;仅当原来基带信号是连续的“10”码时,才可能出现转换后的连续“1”码,而且最多仅2个连续的“0”码或“1”码。
当极性反转时曼彻斯特码会引起译码错误,为解决此问题,又引入了它的衍生码型——差分曼彻斯特码(Differential Manchester Encoding)。差分曼彻斯特编码是曼彻斯特编码的一种修改形式,也是每一码元的1/2码元位置必须进行极性跳变,其不同之处在于不同位置的码元转换方式有些不一样。
对于二进制信号中的第一个码元,与曼彻斯特码的转换方式一样,都是在1/2码元时进行电平极性跳变,即把0码转换成01,把1码转换成10。
在差分曼彻斯特编码中,每一码元中间的跳变也只用来作为同步的时钟信号,所以它也是一种自同步编码。但它的时钟和数据是分离的,便于数据提取。差分曼彻斯特编码主要用于令牌环网。
信号调制与解调
大多数信道不适宜进行基带信号的传输,因为这样的低频信号在传输中会产生很大的衰减和失真。在数字基带传输中,我们知道可以通过数字编码后在信道中直接传输数字信号,但这也仅适用于近距离传输(如在同一局域网中),在复杂网络环境中(如存在不同传输介质和信道类型的网络中),同样不能直接这样传输。因此,需要将基带信号进行调制,变换为适合信道传输的形式,调制是让基带信号去控制载波的某个(或某些)参数,使该参数按照信息的规律进行变化,这就是“调制”过程。“解调”是“调制”的逆过程,即从调制后的信号中恢复原来的调制信号的过程。
调制最通俗的解释就是用一种“能量大”的信号承载(可简单地理解为“背上”)另一种“能量小”的信号进行传播、传输。承载另一种信号的信号我们称为载波或者载波信号,而被承载信号才是我们真正要传播或者传输的信号。
但是,调制不是仅把被承载信号附加在载波信号上就万事大吉了,因为在传输系统中真正发挥作用,需要的还是被承载信号,载波信号只是一个载体,总得让真正有用的被承载信号发挥作用。这时就得通过被承载信号的有关特性来决定载波信号的幅度、频率或者相位。
调制信号通常是低频信号,可以是模拟信号,也可以是数字信号,所以也就有对应的模拟信号调制(或模拟调制)和数字信号调制(或数字调制)。数字调制与模拟调制在本质上没有什么区别,都属于正弦波调制,只是源信号不同。数字调制中的源信号为离散型的脉冲数字信号,而模拟调制中的源信号为连续型的正弦波信号。在此仅介绍数字信号调制技术。
载波就是用来载送有用低频调制信号的信号波,通常是一种高频信号。通过调制技术就可以把调制信号和载波信号进行叠加,使载波信号的某些参数特性(如信号幅度、信号频率或信号相位等)按调制信号变化。具体是载波的哪个参数会随着调制信号发生变化,要视具体的调制类型而定,如果被控制的参数为幅度,则把这种调制称为调幅;如果被控制的参数为频率,则把这种调制称为调频;如果被控制的参数为相位,则把这种调制称为调相。到达接收端后,通过解调技术从已调信号中分离出有用的数据即可。
那为什么要用载波进行调制?因为通常我们要发送的数字信号的频率是比较低的,如果按照本身的频率来传输,信号的衰减比较严重,不利于远距离传输。
之所以要先经过调制过程,就是为了便于低频信号在信道中的远距离、高效传输。
在对数字信号进行载波调制时,我们所采用的也是模拟载波调制中的调幅、调频和调相这三种调制技术。但它们对应已有了另外的名字:ASK(Amplitude Shift Keying,幅度键控)、FSK(Frequency Shift Keying,频率键控)和PSK(Phase Shift Keying,相位键控)。这里之所以都称之为“键控”,是指在这些调制技术中都是用电键进行控制的,这是借用了电报传输中的术语。它们分别对应于利用载波(正弦波)的幅度、频率或相位来承载数字基带信号,可以看做是模拟线性调制和角度调制的特殊情况。
很多童鞋学编程、学通讯都不清楚硬件底层时如何传输数据的,刚好最近整理了些概念和原理,方便大家参阅。如有不妥,欢迎指正!
模拟信号与数字信号
“模拟信号”(analog signal)是“模拟数据”的电平信号表示形式,其信号电平是一个随时间连续变化的(中间没有跳跃)函数曲线(每个周期的曲线是一样的)

而“数字信号”(digital signal)是“数字数据”的信号电平表示形式(由一个个“码元”组成,一个“码元”就包括一个脉冲周期),用两种不同的电平表示二进制的0和1信号所对应的电压脉冲,是离散(非连续变化)的。

基带、频带与宽带
信源信号(也就是信号源发送的信号)经过信源编码之后成为离散的二进制数字信号。我们用一些离散的波形来代替这些数字信号。这些离散的信号可以直接进行传输,或者调制到载波上进行传输。这样就形成了两种最基本的数字信号的传输类型——基带传输和频带传输。在频带传输基础上,通过信道的复用又诞生了一种称为宽带传输的数据传输类型。
基带是指信源发出的,没有经过调制(进行频谱搬移和变换)的原始电信号所固有的频带(频率带宽),也称为基本频带。
而频带是指对基带信号调制后所占用的频率带宽(一个信号所占有的从最高的频率到最低的频率之差)。
所谓“宽带”(Broadband)就是采用比音频(4kHz)更宽的频带,该频带包括了大部分电磁波频谱,是相对前面的“频带”来说的,因为“频带”只具有有限的频率宽度。使用这种宽频带进行的数据传输就称为宽带传输。宽带传输其实与频带传输具有相同的特点,它也需要对信源发出的原始信号进行调制,但它将一个信道分成多个子信道,分别传送音频、视频和数字信号,而且宽带传输中的所有子信道都可以同时发送信号。
基带信号与频带信号
信源发出的没有经过调制的原始电信号(原汁原味)就称为基带信号。基带信号的特点是频率较低,信号频谱是从零频率的直流成分开始的。如果一个信号包含了频率达到无穷大的交流成分和可能的直流成分,则这个信号就是基带信号。
经过调制后的基带信号称为频带信号。频带信号的频率被限制在一个特定的频带中。如果一个信号只包含了一种频率的交流成分,或者有限几种频率的交流成分,我们就称这种信号为频带信号。
根据原始电信号的特征,基带(或频带)信号可分为数字基带(或频带)信号和模拟基带(或频带)信号(相应的,信源也分为数字信源和模拟信源),具体由其信源类型确定。数字基带信号往往包含丰富的低频分量,甚至直流分量。在某些具有低通特性的有线信道中,特别是传输距离不太远的情况下,数字基带信号可以直接传输。
在基带传输中,由于不调制,所以整个信道只传输一种信号,通信信道利用率低。在基带传输中,需要在信源端对数字信号进行编码,在信宿端对编码的数据进行解码恢复,这分别是由编码器和解码器完成的。由于在近距离传输范围内基带信号的衰减不大,从而信号内容不会发生变化。因此在传输距离较近时,计算机网络都采用基带传输类型。大多数的局域网使用基带传输,如以太网、令牌环网等。
而频带传输广泛应用于广域网中,因为在这种网络通信中,往往需要同时发送多种信号(如数据信号、路由信号,以及各种网络控制信号),这时就可以利用高频率的信号来调制低频率信号,以实现同步传输,也提高了信道利用率。由于频带传输中所用的传输频率通常比较高,所以也适用于远距离的广域网通信
“串行传输”和“并行传输”
计算机网络数据通信的数据传输方式可分“串行传输”和“并行传输”两种。
“串行传输”指的是数据流以串行方式一位位地在一条信道上传输。

很显然,串行传输只需要一条传输信道(当然在一个接口中可以有多条这样的串行传输信道),传输速度比较慢,但易于实现、费用低,是目前主要采用的一种传输方式。另外,串行传输存在一个收、发双方如何保持码组或者说字符同步(也就是如果识别一个字符包括哪几个比特位)的问题。这个问题不解决,接收方就不能从接收到的数据流中正确地区分出一个个字符来,因而传输将失去意义。如何解决码组或字符同步的问题,就涉及异步传输方式和同步传输方式了。
采用串行传输方式的典型代表有计算机串行接口(简称串口,对应RS-232C标准),还有如USB接口、SATA(串行ATA)磁盘接口等,
“并行传输”指的是数据以一组或者整个字符的方式在多条并行信道上同时传输。

采用并行传输方式的典型代表有计算机上连接打印机的并口、磁盘ATA(或者IDE)接口等,计算机主板上CPU与其他芯片的数据传输也是采用并行传输方式。
同步传输与异步传输
串行传输接收端存在一个如何从串行数据比特流中正确地划分出发送的一个个字符的问题,也就是字符同步的问题。在串行数据通信中同步问题十分关键。发送端一位一位地把信息通过介质发往接收端,接收端必须识别信息的开始和结束,而且必须知道每一位的持续时间。只有这样,接收端才能从传输线路上正确地取出被传送的数据。根据实现字符同步的方式不同,有同步传输(Synchronous Transmission)和异步传输(Asynchronous Transmission)两种方式。
同步就是指通信双方在传输过程中是同步进行的(也就是接收端与发送端同时开始工作,并且接收端按数据的发送顺序进行接收),同步的依据就是双方有相同的时钟参考,能同时开始数据的发送和接收。通常这个时钟参考是同步时钟线或同一个时钟源。
同步传输是一种以数据块为传输单位(通常是以“帧”为单位的),以相同的时钟参考进行数据传输的模式,因此又称为区块传输。在该传输模式下,每一比特数据的持续传输时间都是相等的,而且在每个字符的传输过程中,两个字符间传输所需等待的时间也是相同的。
另外,在同步传输中的数据块的开始和结尾部分都有一个用于数据帧同步的特殊字符、特定的字节或特定的帧,这具体要视所采用的同步方法而定。同步传输分为面向字符的同步传输、面向比特的同步传输和面向字节的同步传输等几种。

采用同步传输的技术代表有SDH(Synchronous Digital Hierarchy,同步数字系列)、STM(Synchronous Transfer Module,同步传输模块)和HDLC(High level Data Link Control,高级数据链路控制)等。
与下面将要介绍的“异步传输”方式比较,“同步传输”在技术上较复杂,但不需要对每个字符加单独的“起始”和“停止”比特,接收方不必对每个字符进行开始和停止的操作,只需要在检测到帧同步字符时接收它们即可。而且同步传输是以帧为传输单位(异步传输是以字符为传输单位的,一个帧通常有500字节,4000比特)进行传输的,只需在一个数据帧的前后加上标志字符即可,因此传输效率高,常用于较高速的数据传输。
异步传输是指通信双方没有相同的时钟参考(也就是发送端和接收端不同时开始工作),但双方在数据传输速率上是同步的。即指每个字符之间是异步的,但一个字符内的每一位还是同步的。
异步传输是以字符为单位进行数据传输的。在发送每一字符代码的前面均加上一个“起始位”信号(长度为1比特,极性为0),用以标记一个字符的开始;在一个字符代码的最后加上一个“停止位”信号(长度为1或2比特,极性为1),用以标记一个字符的结束。字符位占5~8位,具体取决于数据所采用的字符集,如电报码字符为5位,ASCII码字符为7位。


异步传输的典型代表就是ATM(异步传输模式)技术,目前仍是城域网和广域网中主流的交换技术之一。早期还有一种B-ISDN(宽带ISDN)技术,也是异步传输技术的代表。
在“异步传输”中,发送方可以在任何时刻发送这些比特组,而接收方从不知道它们会在什么时候到达,故不需要同时开始接收。被发送的比特组需进行排除等候。最典型的一个异步传输实例就是我们访问互联网上的网站,点击一个网站,网站服务器一般不会马上响应,而是等它有资源响应时才响应,所以网站打开时往往有些延时。
异步传输的优点是字符同步实现简单,收发双方的时钟信号不需要严格同步。缺点是对每一字符都需加入“起、止”码元,使传输效率降低。例如假设每次传送7比特的信息,每个字符需要另外加一个起始位和一个停止位。另外,异步通信主要处理ASCII编码的信息,这意味着增加了第3个控制位,即奇偶校验位,这样每个字符附加3位控制位,传输效率只有70%。
比特率与波特率
比特率通常又称信息传输速率,是指单位时间内传输的二进制代码的有效位(bit)数,用Rb(注意这里是小写的b)表示。比特率是用来描述可直接在计算机网络数字线路上传输的数字数据的传输速率,常用的单位有bit/s(b/s或bps,每秒比特数)、kbit/s(kb/s或kbps,每秒千比特数)或Mbit/s(Mb/s或Mbps,每秒兆比特数)。但要注意,此处的k和M分别为1000和1 000 000,而不是涉及计算机存储器容量时的1024和1048576。
波特率(Baud rate)是指一个数字信号在被调制后,数字信号对载波的调制速率,也即单位时间内载波参数(如频率、相位等)变化的次数,单位为B。如果是非调制的二进制数字信号,波特率与比特率数值上是相等的,所以波特率通常是针对经过调制后的数字信号传输速率。
波特率的单位为Baud,用RB(注意这里是大写的B)表示。一个数字脉冲,或者直接说是一个二进制位称为一个码元,波特率也可以理解为在单位时间内传输的码元数。这里的码元可以是二进制的,也可以是多进制的。如二进制的字母A的ASCII码是01000001,可用7个脉冲来表示(最高位为校验位,不计入码元中),所以A可认为是由7个码元组成的。若1s内传2400个码元,则波特率为2400B。
对于数字数据,比特率与波特率的关系与数据所采用的进制有关。因为每个码元或符号通常都含有一定比特数的信息量,所以比特率(Rb)与波特率(RB)有如下关系:
Rb=RB×log2M(b/s)
式中的M为符号的进制数,如二进制、八进制、十六进制。例如码元速率为1200B,采用八进制(M=8)时,则可计算出对应的信息速率Rb=1200×log28=3600(b/s);如果采用的是二进制(M=2),则信息速率为Rb=1200×log22=1200(b/s),可见,二进制的波特率和比特率在数值上是相等的。
在采用了数字调制技术的数字通信中,比特率与波特率的关系还与所采用的调制技术有关。
两相调制(单个调制状态对应1个二进制位)的比特率的数值等于波特率的数值;四相调制(单个调制状态对应2个二进制位)的比特率的数值为波特率的数值的2倍;八相调制(单个调制状态对应3个二进制位)的比特率的数值为波特率的数值的3倍;依此类推。
“带宽”是指信道中每秒传输的最大信息量,也就是一个信道的最大数据传输速率,单位也是“位/秒”(b/s或bps)。带宽是一种理想状态(不受任何干扰,没有任何衰减)下的信道传输速率,而上面介绍的“数据传输速率”是指当前实际的数据传输速率,通常情况下“数据传输速率”永远小于或等于“带宽”值(事实上一般不可能等于带宽的,因为传输过程中不可能完全不受干扰,线路性能一般也不可能完全达到理想状态)。
数字信号不失真传输的最大传输速率限制
物理层的任何一个信道,它所能承受的信号频率(或者说是信道带宽)是有限的,就像任何一条河流只能承受一定峰值的水流量一样。在信道中,超出限定的频率范围的信号都将被直接滤出,不能通过信道,就像河流中任何超出它流速限制的水流量最终不能形成实际速率的水流量一样。
在计算数字信道中最大传输速率方面,有两个非常有名的准则或定理,那就是奈奎斯特准则(简称奈氏准则)和香农公式。
由于数字信号(这里特指没有被调制的原始数字信号,也就是上面所说的数字基带信号)的频带(这里是指信号的频率带宽)可以非常宽(从直流一直到无限高的频率),但其主要能量集中在低频段,而且数据通信中的电缆传输信道只允许比较低的频率成分通过理想低通信道,高频成分将被滤去,这就造成了输出波形的失真。失真的输出波形顶部变圆,底部变宽(称为波形拖尾),使得一个码元的波形展宽到其他码元位置,影响到其他码元,这种影响称为码间干扰。
理想“低通信道”是指只要信号频率不超过某个上限值都能够不失真地通过此信道;而频率超过该上限值的所有高频分量都不能通过该信道。与之相对的还有一种称为理想“带通矩形信道”,它是指仅允许在上下限之间的信号频率成分不失真地通过,其他频率成分不能通过。
要使信道中传输的数字信号不失真,信道中的数据传输速率必须限制在某个范围之内,这又与信道类型有关。1924年,美国著名物理学家奈奎斯特(Nyquist),经过多次实验证明,为了确保数字信号不失真传输,在理想低通信道(基带传输中的信道)下实际的最高码元传输速率(即无码间干扰的最高波特率)必须在下式计算结果之内:
最高码元传输速率(MaxRB)=2W
式中W是理想低通信道的带宽,单位为赫(Hz),MaxRB为最高码元传输速率,单位为Raud(波特)。这就是著名的奈奎斯特第一准则,其指出了在理想低通信道(也就是4.2.4节中介绍的基带传输中的信道)中,为了确保数字信号的不失真传输,信道带宽和最大码元传输速率之间的关系。
以上奈奎斯特第一准则描述了有限带宽、无噪声信道的最大数据传输速率与信道带宽的关系。美国的另一位著名物理学家——克劳德·香农(Claude Elwood Shannon)也在数据通信领域有权威的发现,那就是“香农公式”。这个公式描述了有限信道带宽、有随机热噪声信道(更接近真实环境)的最大传输速率与信道带宽、信噪比(信号平均功率与噪声功率之比)之间的关系。香农公式指出:在有随机热噪声的信道上传输数据信
号时,最大数据传输速率Rmax与信道带宽B、信噪比S/N的关系如下所示:
Rmax=B×log2(1+S/N)
式中Rmax的单位为bps,信道带宽B的单位为Hz,信噪比S/N通常用dB(分贝)表示,可用10×log10(S/N)公式来计算信噪比的分贝数。若已知S/N=1000,则根据公式可很快得出用分贝数表示的信噪比为30dB。如果再已知信道带宽B=3000Hz,则Rmax≈30kbps。它表示对于带宽只有3000Hz的通信信道,信噪比在30dB时,无论数据采用二进制或更多的离散电平值表示,都不能用越过30kbps的数据传输速率。
模拟信号不失真还原的最小采样频率限制
在计算机设备中只能接收数字信号,如果在信道中传输的是模拟信号(通过公共交换电话网络进行的远程网络连接的电话线路中传输的都是模拟信号),在接收端必须进行模/数转换,生成数字信号;同样如果将在一个计算机设备中的数字信号还原到某条模拟线路中进行传输,则又要进行数/模转换,还原成原来的模拟信号。这里最关键的是由模拟信号转换成数字信号,因为在这个转换过程中要确保数据不失真。
因为模拟信号是随时间连续变化的,而数字信号则是离散的,所以在模/数转换过程中,就需要离散地在模拟信号上抽取一定的信号样本,形成数字信号样本,以便可以不失真地代表原始数据本身,也使得抽取的数字信号样本在需要时能还原为原始的模拟信号。这就涉及一个“采样频率”(简单地说就是每隔多少时间提取一次信号波)的问题。
要确保信号不失真的恢复,最低的采样率需要达到多少呢?采样过程所应遵循的规律称为采样定理,又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系,是连续信号离散化的基本依据。
只要这些采样点的时间间隔Δt≤1/2F,便可根据各采样值完全恢复原来的信号f(t)。简单地讲就是,在进行模拟/数字信号的转换过程中,当采样频率fs,max大于或等于信号中最高频率fmax的2倍时(fs,max≥2fmax),采样之后的数字信号就可完整地保留原始信号中的信息,原来的连续信号就可以从采样样本中完全重建出来,否则采
样信号后的频率将会混叠。一般实际应用中保证采样频率为信号最高频率的5~10倍。
由以上定理可以得知,如果已知信号的最高频率fH,就可以得出保证完全重建信号的最低采样频率是2fH。相反,如果已知采样频率,则可以得出保证信号完全重建所允许的最高信号频率。但要注意的是,这里有一个条件,那就是被采样的信号必须是带限的,也就是是有限带宽的,信号中高于某一给定频率的成分必须是0,或者至少非常接近0。只有这样,在重建信号时这些频率成分的影响才可以忽略不计。如果被采样的信号不是带限的,采样后信号的频率就会产生重叠,即高于采样频率一半的成分将被重建成低于采样频率一半的信号,最终导致信号不能被完全恢复。
数字基带信号编码
数字基带传输模式中传输的信号是要经过编码的原始数字信号。但数字基带信号的类型有很多,常见的有矩形脉冲、三角波、高斯脉冲和余弦脉冲等。其中最常用的是矩形脉冲,因为矩形脉冲易于形成和变换。
在矩形脉冲数字信号中主要有以下四种波形:单极性不归零波形、单极性归零波形、双极性不归零波形、双极性归零波形。




信道编码
在实际的基带传输系统中,并不是所有编码类型的电信号波形都能在信道中传输。例如上节介绍的含有直流分量和较丰富低频分量的单极性基带波形就不适宜在低频传输特性差的信道中传输,因为其功率较弱,在传输过程中有可能造成信号严重畸变。另外,当信息代码中包含有长串的连续“1”或“0”时,非归零波形呈现出连续的固定电平,会出现无法获取同步的问题。单极性归零码在传送连续“0”信息代码时也会存在同样的问题。因此,信息码在进行传输之前,必须经过码型变换,变换为适用于信道传输的码型,这就是通常所说的传输码,也称线路码或信道编码。
传输码型的选择原则:
一是要能从基带信号中提取定时信息(位同步脉冲信息),所以要求传输码型应含有(或者经变换后含有)时钟频率分量(不能出现0电平),且编码转换后不能出现过多的连续“0”码或“1”码,否则提取的时钟信号就会很不稳定,引起同步偏移;
二是要无直流分量、低频成分少,否则影响信号在信道中的传输;
三是信号中高频分量要尽量少,以节省传输频带并减少码间串扰。
常见的传输码型有:传号反转交替码(AMI码)、三阶高密度双极性码(HDB3码)、传号反转码(CMI码)、数字双相码(曼彻斯特码)和差分曼彻斯特码。

AMI码的优点是:由于“1”码元采用了正、负电平交替,所以AMI码的有信号部分的频谱中不含直流成分,高频和低频成分也很少。另外,AMI码的编译码电路简单,便于利用传号极性交替规律观察误码情况。鉴于这些优点,AMI码是CCITT建议采用的传输码型之一。
AMI码的不足是:当原二进制信号代码出现连续的“0”码时,信号电平会长时间不变,造成提取定时信号的困难(也就是同步比较困难),解决连续“0”码问题的有效方法之一是采用后面要介绍的HDB3码,它是AMI码的改进码型。

HDB3码除保持了前面介绍的AMI码的优点外,同时还将连续“0”码限制在3个以内,更有利于位定时信号的提取。HDB3码是应用最为广泛的码型,已成为CCITT协会推荐使用的基带传输码型之一。

CMI码具有一定的检测错误的能力,因为“1”码交替地用“11”和“00”来表示,而“0”又固定用“01”表示,所以正常情况下,转换后的编码“10”是不可能在信道中出现的,连续的“00”或“11”也是不可能出现的,这样一来就可以用来检测因信道传输而产生的错误。但是CMI码不能纠错。CMI码也没有直流分量(没有零电平,只有正、页电平),且有频繁出现的波形跳变,便于恢复定时信号(也就是便于同步)。

曼彻斯特码的优点也是无直流分量(全部转换为双极性电平,无零电平),最长连续“0”码或连续“l”码的个数仅为2,非常容易实现同步,编译码电路简单。因为如果原来基带信号是连续的“1”码,转换后都为“10”两个码了,不会出现连续的“1”码,如果原来基带信号是连续的“0”码,转换后都为“01”两个码了,不会出现连续的“1”码或“0”码。仅当原来基带信号是连续的“01”码时,才可能出现转换后的连续“0”码;仅当原来基带信号是连续的“10”码时,才可能出现转换后的连续“1”码,而且最多仅2个连续的“0”码或“1”码。
当极性反转时曼彻斯特码会引起译码错误,为解决此问题,又引入了它的衍生码型——差分曼彻斯特码(Differential Manchester Encoding)。差分曼彻斯特编码是曼彻斯特编码的一种修改形式,也是每一码元的1/2码元位置必须进行极性跳变,其不同之处在于不同位置的码元转换方式有些不一样。
对于二进制信号中的第一个码元,与曼彻斯特码的转换方式一样,都是在1/2码元时进行电平极性跳变,即把0码转换成01,把1码转换成10。
在差分曼彻斯特编码中,每一码元中间的跳变也只用来作为同步的时钟信号,所以它也是一种自同步编码。但它的时钟和数据是分离的,便于数据提取。差分曼彻斯特编码主要用于令牌环网。
信号调制与解调
大多数信道不适宜进行基带信号的传输,因为这样的低频信号在传输中会产生很大的衰减和失真。在数字基带传输中,我们知道可以通过数字编码后在信道中直接传输数字信号,但这也仅适用于近距离传输(如在同一局域网中),在复杂网络环境中(如存在不同传输介质和信道类型的网络中),同样不能直接这样传输。因此,需要将基带信号进行调制,变换为适合信道传输的形式,调制是让基带信号去控制载波的某个(或某些)参数,使该参数按照信息的规律进行变化,这就是“调制”过程。“解调”是“调制”的逆过程,即从调制后的信号中恢复原来的调制信号的过程。
调制最通俗的解释就是用一种“能量大”的信号承载(可简单地理解为“背上”)另一种“能量小”的信号进行传播、传输。承载另一种信号的信号我们称为载波或者载波信号,而被承载信号才是我们真正要传播或者传输的信号。
但是,调制不是仅把被承载信号附加在载波信号上就万事大吉了,因为在传输系统中真正发挥作用,需要的还是被承载信号,载波信号只是一个载体,总得让真正有用的被承载信号发挥作用。这时就得通过被承载信号的有关特性来决定载波信号的幅度、频率或者相位。
调制信号通常是低频信号,可以是模拟信号,也可以是数字信号,所以也就有对应的模拟信号调制(或模拟调制)和数字信号调制(或数字调制)。数字调制与模拟调制在本质上没有什么区别,都属于正弦波调制,只是源信号不同。数字调制中的源信号为离散型的脉冲数字信号,而模拟调制中的源信号为连续型的正弦波信号。在此仅介绍数字信号调制技术。
载波就是用来载送有用低频调制信号的信号波,通常是一种高频信号。通过调制技术就可以把调制信号和载波信号进行叠加,使载波信号的某些参数特性(如信号幅度、信号频率或信号相位等)按调制信号变化。具体是载波的哪个参数会随着调制信号发生变化,要视具体的调制类型而定,如果被控制的参数为幅度,则把这种调制称为调幅;如果被控制的参数为频率,则把这种调制称为调频;如果被控制的参数为相位,则把这种调制称为调相。到达接收端后,通过解调技术从已调信号中分离出有用的数据即可。
那为什么要用载波进行调制?因为通常我们要发送的数字信号的频率是比较低的,如果按照本身的频率来传输,信号的衰减比较严重,不利于远距离传输。
之所以要先经过调制过程,就是为了便于低频信号在信道中的远距离、高效传输。
在对数字信号进行载波调制时,我们所采用的也是模拟载波调制中的调幅、调频和调相这三种调制技术。但它们对应已有了另外的名字:ASK(Amplitude Shift Keying,幅度键控)、FSK(Frequency Shift Keying,频率键控)和PSK(Phase Shift Keying,相位键控)。这里之所以都称之为“键控”,是指在这些调制技术中都是用电键进行控制的,这是借用了电报传输中的术语。它们分别对应于利用载波(正弦波)的幅度、频率或相位来承载数字基带信号,可以看做是模拟线性调制和角度调制的特殊情况。

 举报
举报















 举报
举报

