随着数字通信系统的发展,语音通信已成为人们日常生活的一部分,手机,电话和网络语音通信等已经逐渐深入人们的日常生活,通信技术是信息技术中极重要的组成部分。
语音是人体发音器官通过声带抖动发出的具有特殊含义的,并能够传达人类交流信息的特殊的声音。语音作为语言的特殊载体,以语音的形式存在于在人类发明文字之前。世界上目前存在无文字的语言的情形,却没有无语音的语言,由此可见,语音在语言中起决定性的作用。作为语言特殊载体的语音在语言中起着不可替代的作用,而语言是语音和文字意义互相结合的符号系统。
由于语言的特殊性,但其作为和普通的声音有着本质的区别特殊声音。语音主要有四个要素构成,主要包括音长、音强、音色、音高。音长指的是声波振动持续时间的长短;其中音强指的是声波振幅的大小;音色指的是声音的特色和本质,即音质;音高指的是声波频率,即每秒钟振动次数的多少。
在语音通信系统中,语音信号的传输过程往往会受到环境噪声或者传输设备自身固有噪声的干扰,从而影响语音信号传输的质量。
因此,研究语音通信系统的算法有着十分重要的意义,通过对语音通信系统各个模块的仿真研究,从而实现将语音信号有效、可靠的从发送端传输到接收端。
1.2国内外研究现状
目前,国内外关于语音通信系统的研究成果主要有如下几个方面:
第一、语音信号传输的数字通信系统的实现
关于语音信号传输的数字通信系统的研究,主要有基于DSP的数字通信系统的实现以及基于FPGA的数字通信系统的实现。目前DSP公司主要有主要有TI公式的DSP芯片以及AD公司的DSP芯片,通过DSP芯片可以实现数字语音信号处理算法。目前较为常用的DSP芯片TMS320CX系列和ADSP 系列。此外,FPGA技术也在数字信号处理领域有着使用广泛的应用,FPGA技术具有高灵活、高性能、低功耗、低成本等优势。FPGA芯片较常见到的有Xilinx 公司的FPGA 系列产品和 Altera 公司的 FPGA 系列产品。
第二、语音信号去噪声的研究
语音降噪技术,最早是采用模拟滤波器搭建相应的滤波电路来实现语音信号的降噪。但是,当语音信号的噪声出现突变的时候,传统的模拟滤波器就无法实时的满足新的噪声变化情况,这个极大的影响了实际价值。国内关于语言信号的降噪技术的研究主要开始于上世纪50年代,主要基于模拟技术来实现语音降噪的功能,采用这种方法,其性能大概可以提升语音信号的质量为8 db到12db之间。但是这种方法无法在大噪声下实现有效的语音信号降噪的效果。到80年,主要开始使用声音平衡原理的方式降低通讯中的噪声,但是这种方法会比较明显的干扰整个系统的工作性能。到了上世纪90年代,出现了动态降噪技术,这个技术可以根据实际的语音信号的幅度大小进行实时动态的进行噪声的滤波。
第三、语音信号处理编译码算法的研究
在进行语音信号通信的时候,为了提升系统的性能,需要引入编码技术,目前关于语音信号编码技术主要有统信源编码如 PCM 码及其相关变换的编码,先进的信道编码turbo 码、LDPC 码。
通信通常是发信者与收信者之间消息的往来,数字语音通信则是指将语音(模拟)信号转换成数字电信号进行传输的过程,其基本结构和通信系统基本结构一致,主要包括信源、发送设备、信道、接收设、信宿等几部分,其原理框图如图2.1所示。

图2.1 通信系统基本结构框图
下面我们将对语音通信系统的各个模块进行理论分析。整个语音通信系统的结构如下图所示:
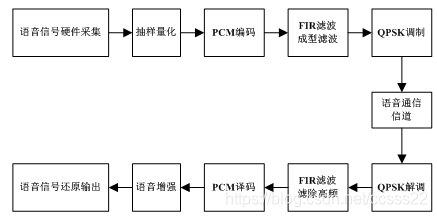
图2.2 语音通信系统结构框图
2.2语音信号的信道特征分析
信道中的干扰主要分为:有源干扰( 噪声)、无源干扰(传输特性不良),信道中的噪声:信道中存在的不需要的电信号,又称加性干扰。噪声的种类有很多种,根据噪声的干扰特点,可以分为分为加性噪声和乘性噪声。加性噪声是一种表现为噪声信号对语音信号在时域进行相加的行为;而乘性噪声则反应了噪声和语音在频域是相乘的关系,在时域和语音则是卷积的关系。下面主要对周期性噪声干扰,脉冲噪声干扰以及宽带噪声干扰进行简介。
周期性噪声:周期性噪声周期性运转的机械设备。对于周期性噪声一般可以通过固定滤波器,自适应滤波器和傅里叶变换滤波器进行滤波,主要运用功率谱检测的方式,故周期性噪声对语音信号的影响很小。
脉冲噪声:脉冲信号是在时域波形中突然出现的窄脉冲的总称。在时域范围内滤除脉冲噪声的方法主要方法:根据预先计算好的语音信号的平均幅度值来计算判决门限值,当幅度超出预设门限值时,则认为该信号为脉冲噪声,随即对该信号进行衰减,直到完全消除为止。
带宽噪声:带宽噪声具有噪声频谱遍布于语音信号频谱之中的特点,可以假设其噪声为高斯噪声和白噪声。
根据实际的语音信号的分析可知,语音信号主要有下面两个特点:
第一,语音信号具有短时性特点,即语音信号的特征是随着时间的变化而变化,但是在短时间内,语音信号保持一定的平稳性。
第二,语音信号的频谱能量主要集中在300-3400Hz的范围内。
图2.2为语音信号的时域波形图和频域图:
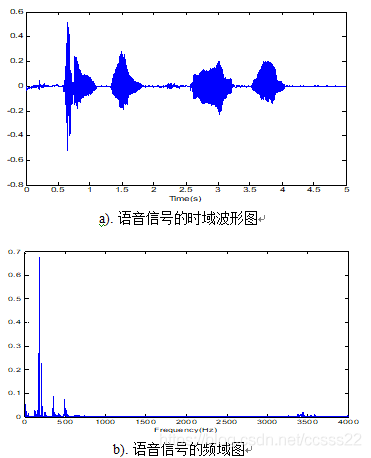
图2.3 语音信号的时域图和频谱图
在将语音信号进行采集之前,先进行预滤波,预滤波的主要作用是对语音信号进行防混叠处理。预滤波主要作用有如下两点:
第一,抑制输入信号各领域分量中频率超出fs/2的所有分量(fs为采样频率),以防止混叠干扰。
第二,抑制50Hz的电源工频干扰。
采样即信号在时间上的离散化,采样时必须要注意满足奈奎斯特定理,即采样频率fs必须以高于受测信号的最高频率两倍以上的速度进行取样,才能正确地重建。在实际语音信号采样过程中,必须选择合理的采样频率。当采样频率过高,对固定长度(T)的信号,采集到过大的数据量(N=T/△t),给计算机增加不必要的计算工作量和存储空间。当采样频率过低,采样点间隔过远,则离散信号不足以反映原有信号波形特征,无法使信号复原,造成信号混淆。
通常情况,采样必须满足奈奎斯特采样定律:
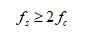
(2.1)
当系统的采样频率大于等于两倍的信号频率的时候,可以保证原始信号特征的前提下,最小的采样频率。
在MATLAB中,我们直接使用wavrecord命令功能函数采集音频信号。wavrecord的使用方法如下所示:
wavrecord(n,fs,ch,dtype);
其中:
n:采样点数,决定录音长度;
fs:采样频率,为8000Hz、11025Hz、22050Hz、44100Hz之一,默认值为11025Hz;
ch:样本采集通道,1为单声道,2为双声道,默认值为1;
dtype:采样数据存储格式,即每个样本的解析度。
采集到语音信号之后,需要对语音信号进行分析,如语音信号的时域分析、频谱分析、语谱图分析以及加噪滤波等处理。
通过这个指令,我们得到如下的采集波形:
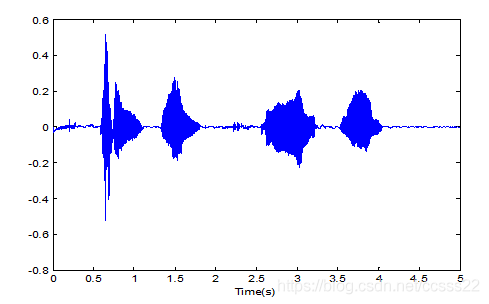
图3.2 采集到的语音信号
根据本文第二章的介绍,我们将对采集到的语音信号进行A率量化,具体实现过程如下所示:
•A律压缩的MATLAB代码如下所示:
function ypcm=alaw(yn)
x=yn;
s=sign(x);
x=abs(x);
ypcm=zeros(length(x),1);
%进行基于13折线的分段映射
for i=1:length(x)
if x(i)《1/64 %序列值位于第1和第2折线
ypcm(i)=16*x(i);
elseif x(i)《1/32 %序列值位于第3折线
ypcm(i)=8*x(i)+1/8;
elseif x(i)《1/16 %序列值位于第4折线
ypcm(i)=4*x(i)+2/8;
elseif x(i)《1/8 %序列值位于第5折线
ypcm(i)=2*x(i)+3/8;
elseif x(i)《1/4 %序列值位于第6折线
ypcm(i)=x(i)+4/8;
elseif x(i)《1/2 %序列值位于第7折线
ypcm(i)=1/2*x(i)+5/8;
else %序列值位于第8折线
ypcm(i)=1/4*x(i)+6/8;
end
end
ypcm=ypcm.*(2^7);
ypcm=floor(ypcm);
ypcm=ypcm.*s;
•A律解压缩的MATLAB代码如下所示:
function ypcm=unalaw(name)
x=name;
s=sign(x);
x=abs(x);
%归一化
x=x/128;
ypcm=zeros(length(x),1);
%基于13折线的分段解码映射
for i=1:length(x)
if x(i)《2/8 %序列值位于第1和第2折线
ypcm(i)=1/16*x(i);
elseif x(i)《3/8 %序列值位于第3折线
ypcm(i)=1/8*(x(i)-1/8);
elseif x(i)《4/8 %序列值位于第4折线
ypcm(i)=1/4*(x(i)-2/8);
elseif x(i)《5/8 %序列值位于第5折线
ypcm(i)=1/2*(x(i)-3/8);
elseif x(i)《6/8 %序列值位于第6折线
ypcm(i)=x(i)-4/8;
elseif x(i)《7/8 %序列值位于第7折线
ypcm(i)=2*(x(i)-5/8);
else %序列值位于第8折线
ypcm(i)=4*(x(i)-6/8);
end
end
ypcm=ypcm.*s;
我们可以得到仿真结果如下所示:
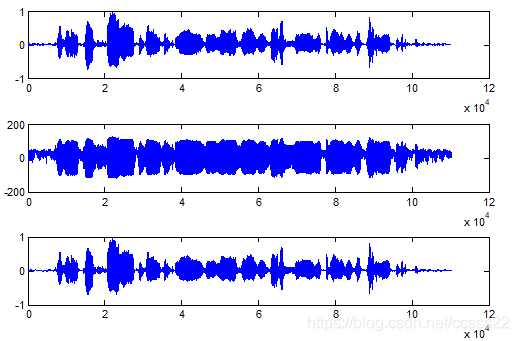
图3.3 A律压缩,解压缩仿真图(原始信号,压缩后的信号,解压后的信号)
对压缩和解压缩后的信号做误差分析,我们可以得到如下的结果。
图3.3 A律压缩,解压缩仿真图(原始信号,压缩后的信号,解压后的信号)
对压缩和解压缩后的信号做误差分析,我们可以得到如下的结果。
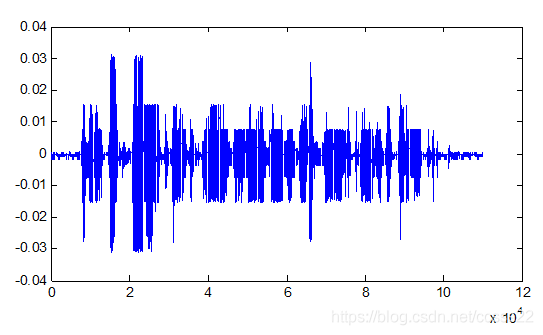
图3.4 A律压缩,解压缩误差波形图
从图3.4的仿真结果可知,通过A率量化压缩和解压缩之后,系统的误差为0.03以内,这说明系统误差较小,可以满足实际的通信需求。
3.3 基于FIR的数字滤波模块的设计与仿真
在MATLAB中,我们使用Filter函数进行仿真,首先,我们得到成形滤波器的系数为:
0.02122066,0.00773409,-0.03751318,-0.07842133,
-0.05305165,0.07842133,0.28931623,0.48724768,
0.56830989,0.48724768,0.28931623,0.07842133,
-0.05305165,-0.07842133,-0.03751318,0.00773409,
0.02122066;
分别得到如下两路信号:
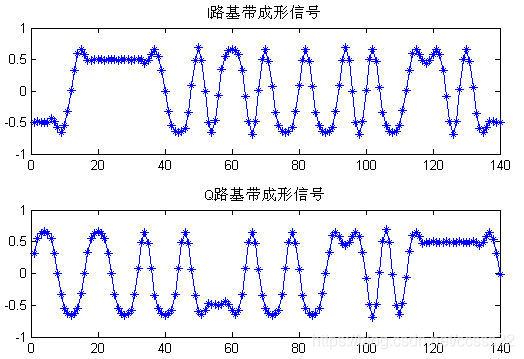
图3.5 通过FIR滤波器的两路基带信号
I,Q两路基带信号通过成形滤波以后的成形信号。
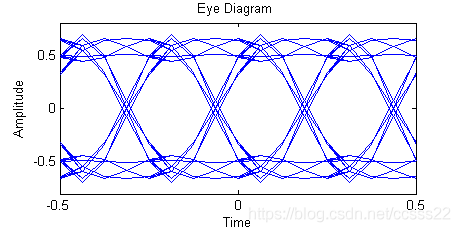
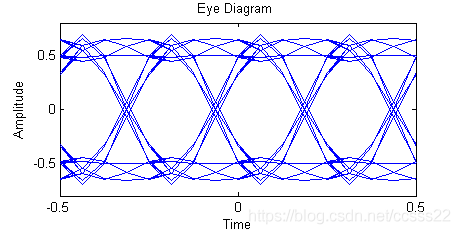
图3.6 通过FIR滤波器的I,Q两路眼图信号
3.4 基于QPSK的语音信号调制解调模块的设计与仿真
这里,我们对语音信号的QPSK调制解调进行仿真,整个过程为,将抽样量化后的二进制数字信号进行成型滤波,然后进行正交调制,从而获得QPSK中频信号。其MATLAB仿真效果如下图所示:
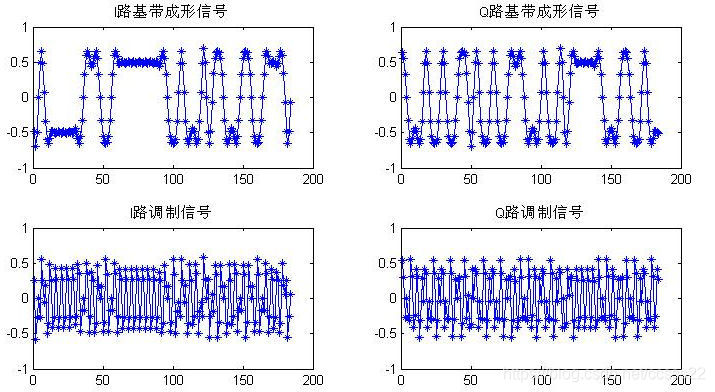
图3.7QPSK调制信号
其中频信号如下所示:
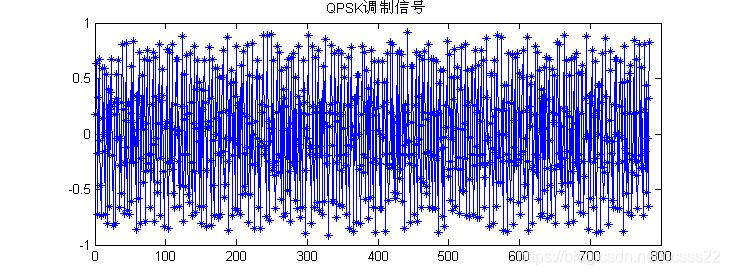
图3.8 调制后的语音发送信号
QPSK调制解调的MATLAB算法程序如下所示:
%调制
function [I_Data,Q_Data] = QPSK_signal(len);
%QPSK信号源
%I_Data=randint(len,1)*2-1;
%Q_Data=randint(len,1)*2-1;
%s=I_Data + j*Q_Data;
I_Data = randint(len,1)*2-1;
Q_Data = randint(len,1)*2-1;
%解调
n=1000;
x = randint(n,1); %产生信源。
h = modem.pskmod (4); %产生调制句柄
y = modulate(h,x); %对信号进行调制
g = modem.pskdemod (h) %产生解调句柄
z = demodulate(g,y); %进行解调
根据第二章的理解介绍,使用本文所提出的结合VSLMS滤波和子空间滤波的语音降噪算法进行仿真,通过仿真,分别在信噪比在5dB和15dB下进行仿真分析,通过仿真,我们可以得到如下的仿真效果:
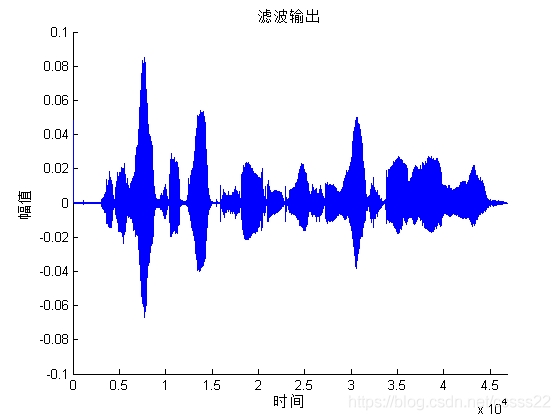
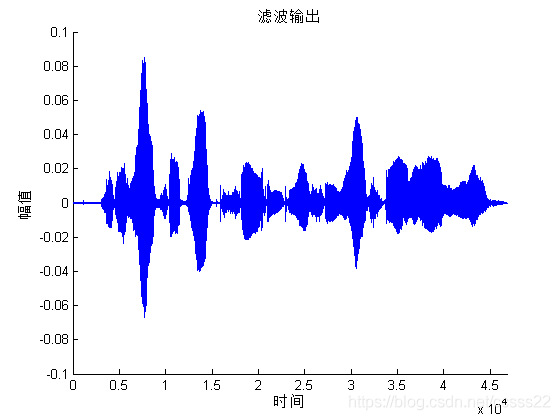
图3.9基于VSLMS算法和子空间降噪算法的滤波效果(SNR=5dB,15dB)
下面,我们分别对三种滤波算法前后误差的比较。
我们将最后滤波输出的有效信号和有用元音信号做比较,对信号首先做归一化处理,然后计算输出信号和有用信号的相对误差。从图中可以看出,其最后的误差在10%以内,因此,滤波性能得到了明显的改善。
随着数字通信系统的发展,语音通信已成为人们日常生活的一部分,手机,电话和网络语音通信等已经逐渐深入人们的日常生活,通信技术是信息技术中极重要的组成部分。
语音是人体发音器官通过声带抖动发出的具有特殊含义的,并能够传达人类交流信息的特殊的声音。语音作为语言的特殊载体,以语音的形式存在于在人类发明文字之前。世界上目前存在无文字的语言的情形,却没有无语音的语言,由此可见,语音在语言中起决定性的作用。作为语言特殊载体的语音在语言中起着不可替代的作用,而语言是语音和文字意义互相结合的符号系统。
由于语言的特殊性,但其作为和普通的声音有着本质的区别特殊声音。语音主要有四个要素构成,主要包括音长、音强、音色、音高。音长指的是声波振动持续时间的长短;其中音强指的是声波振幅的大小;音色指的是声音的特色和本质,即音质;音高指的是声波频率,即每秒钟振动次数的多少。
在语音通信系统中,语音信号的传输过程往往会受到环境噪声或者传输设备自身固有噪声的干扰,从而影响语音信号传输的质量。
因此,研究语音通信系统的算法有着十分重要的意义,通过对语音通信系统各个模块的仿真研究,从而实现将语音信号有效、可靠的从发送端传输到接收端。
1.2国内外研究现状
目前,国内外关于语音通信系统的研究成果主要有如下几个方面:
第一、语音信号传输的数字通信系统的实现
关于语音信号传输的数字通信系统的研究,主要有基于DSP的数字通信系统的实现以及基于FPGA的数字通信系统的实现。目前DSP公司主要有主要有TI公式的DSP芯片以及AD公司的DSP芯片,通过DSP芯片可以实现数字语音信号处理算法。目前较为常用的DSP芯片TMS320CX系列和ADSP 系列。此外,FPGA技术也在数字信号处理领域有着使用广泛的应用,FPGA技术具有高灵活、高性能、低功耗、低成本等优势。FPGA芯片较常见到的有Xilinx 公司的FPGA 系列产品和 Altera 公司的 FPGA 系列产品。
第二、语音信号去噪声的研究
语音降噪技术,最早是采用模拟滤波器搭建相应的滤波电路来实现语音信号的降噪。但是,当语音信号的噪声出现突变的时候,传统的模拟滤波器就无法实时的满足新的噪声变化情况,这个极大的影响了实际价值。国内关于语言信号的降噪技术的研究主要开始于上世纪50年代,主要基于模拟技术来实现语音降噪的功能,采用这种方法,其性能大概可以提升语音信号的质量为8 db到12db之间。但是这种方法无法在大噪声下实现有效的语音信号降噪的效果。到80年,主要开始使用声音平衡原理的方式降低通讯中的噪声,但是这种方法会比较明显的干扰整个系统的工作性能。到了上世纪90年代,出现了动态降噪技术,这个技术可以根据实际的语音信号的幅度大小进行实时动态的进行噪声的滤波。
第三、语音信号处理编译码算法的研究
在进行语音信号通信的时候,为了提升系统的性能,需要引入编码技术,目前关于语音信号编码技术主要有统信源编码如 PCM 码及其相关变换的编码,先进的信道编码turbo 码、LDPC 码。
通信通常是发信者与收信者之间消息的往来,数字语音通信则是指将语音(模拟)信号转换成数字电信号进行传输的过程,其基本结构和通信系统基本结构一致,主要包括信源、发送设备、信道、接收设、信宿等几部分,其原理框图如图2.1所示。

图2.1 通信系统基本结构框图
下面我们将对语音通信系统的各个模块进行理论分析。整个语音通信系统的结构如下图所示:

图2.2 语音通信系统结构框图
2.2语音信号的信道特征分析
信道中的干扰主要分为:有源干扰( 噪声)、无源干扰(传输特性不良),信道中的噪声:信道中存在的不需要的电信号,又称加性干扰。噪声的种类有很多种,根据噪声的干扰特点,可以分为分为加性噪声和乘性噪声。加性噪声是一种表现为噪声信号对语音信号在时域进行相加的行为;而乘性噪声则反应了噪声和语音在频域是相乘的关系,在时域和语音则是卷积的关系。下面主要对周期性噪声干扰,脉冲噪声干扰以及宽带噪声干扰进行简介。
周期性噪声:周期性噪声周期性运转的机械设备。对于周期性噪声一般可以通过固定滤波器,自适应滤波器和傅里叶变换滤波器进行滤波,主要运用功率谱检测的方式,故周期性噪声对语音信号的影响很小。
脉冲噪声:脉冲信号是在时域波形中突然出现的窄脉冲的总称。在时域范围内滤除脉冲噪声的方法主要方法:根据预先计算好的语音信号的平均幅度值来计算判决门限值,当幅度超出预设门限值时,则认为该信号为脉冲噪声,随即对该信号进行衰减,直到完全消除为止。
带宽噪声:带宽噪声具有噪声频谱遍布于语音信号频谱之中的特点,可以假设其噪声为高斯噪声和白噪声。
根据实际的语音信号的分析可知,语音信号主要有下面两个特点:
第一,语音信号具有短时性特点,即语音信号的特征是随着时间的变化而变化,但是在短时间内,语音信号保持一定的平稳性。
第二,语音信号的频谱能量主要集中在300-3400Hz的范围内。
图2.2为语音信号的时域波形图和频域图:

图2.3 语音信号的时域图和频谱图
在将语音信号进行采集之前,先进行预滤波,预滤波的主要作用是对语音信号进行防混叠处理。预滤波主要作用有如下两点:
第一,抑制输入信号各领域分量中频率超出fs/2的所有分量(fs为采样频率),以防止混叠干扰。
第二,抑制50Hz的电源工频干扰。
采样即信号在时间上的离散化,采样时必须要注意满足奈奎斯特定理,即采样频率fs必须以高于受测信号的最高频率两倍以上的速度进行取样,才能正确地重建。在实际语音信号采样过程中,必须选择合理的采样频率。当采样频率过高,对固定长度(T)的信号,采集到过大的数据量(N=T/△t),给计算机增加不必要的计算工作量和存储空间。当采样频率过低,采样点间隔过远,则离散信号不足以反映原有信号波形特征,无法使信号复原,造成信号混淆。
通常情况,采样必须满足奈奎斯特采样定律:
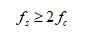
(2.1)
当系统的采样频率大于等于两倍的信号频率的时候,可以保证原始信号特征的前提下,最小的采样频率。
在MATLAB中,我们直接使用wavrecord命令功能函数采集音频信号。wavrecord的使用方法如下所示:
wavrecord(n,fs,ch,dtype);
其中:
n:采样点数,决定录音长度;
fs:采样频率,为8000Hz、11025Hz、22050Hz、44100Hz之一,默认值为11025Hz;
ch:样本采集通道,1为单声道,2为双声道,默认值为1;
dtype:采样数据存储格式,即每个样本的解析度。
采集到语音信号之后,需要对语音信号进行分析,如语音信号的时域分析、频谱分析、语谱图分析以及加噪滤波等处理。
通过这个指令,我们得到如下的采集波形:

图3.2 采集到的语音信号
根据本文第二章的介绍,我们将对采集到的语音信号进行A率量化,具体实现过程如下所示:
•A律压缩的MATLAB代码如下所示:
function ypcm=alaw(yn)
x=yn;
s=sign(x);
x=abs(x);
ypcm=zeros(length(x),1);
%进行基于13折线的分段映射
for i=1:length(x)
if x(i)《1/64 %序列值位于第1和第2折线
ypcm(i)=16*x(i);
elseif x(i)《1/32 %序列值位于第3折线
ypcm(i)=8*x(i)+1/8;
elseif x(i)《1/16 %序列值位于第4折线
ypcm(i)=4*x(i)+2/8;
elseif x(i)《1/8 %序列值位于第5折线
ypcm(i)=2*x(i)+3/8;
elseif x(i)《1/4 %序列值位于第6折线
ypcm(i)=x(i)+4/8;
elseif x(i)《1/2 %序列值位于第7折线
ypcm(i)=1/2*x(i)+5/8;
else %序列值位于第8折线
ypcm(i)=1/4*x(i)+6/8;
end
end
ypcm=ypcm.*(2^7);
ypcm=floor(ypcm);
ypcm=ypcm.*s;
•A律解压缩的MATLAB代码如下所示:
function ypcm=unalaw(name)
x=name;
s=sign(x);
x=abs(x);
%归一化
x=x/128;
ypcm=zeros(length(x),1);
%基于13折线的分段解码映射
for i=1:length(x)
if x(i)《2/8 %序列值位于第1和第2折线
ypcm(i)=1/16*x(i);
elseif x(i)《3/8 %序列值位于第3折线
ypcm(i)=1/8*(x(i)-1/8);
elseif x(i)《4/8 %序列值位于第4折线
ypcm(i)=1/4*(x(i)-2/8);
elseif x(i)《5/8 %序列值位于第5折线
ypcm(i)=1/2*(x(i)-3/8);
elseif x(i)《6/8 %序列值位于第6折线
ypcm(i)=x(i)-4/8;
elseif x(i)《7/8 %序列值位于第7折线
ypcm(i)=2*(x(i)-5/8);
else %序列值位于第8折线
ypcm(i)=4*(x(i)-6/8);
end
end
ypcm=ypcm.*s;
我们可以得到仿真结果如下所示:

图3.3 A律压缩,解压缩仿真图(原始信号,压缩后的信号,解压后的信号)
对压缩和解压缩后的信号做误差分析,我们可以得到如下的结果。
图3.3 A律压缩,解压缩仿真图(原始信号,压缩后的信号,解压后的信号)
对压缩和解压缩后的信号做误差分析,我们可以得到如下的结果。

图3.4 A律压缩,解压缩误差波形图
从图3.4的仿真结果可知,通过A率量化压缩和解压缩之后,系统的误差为0.03以内,这说明系统误差较小,可以满足实际的通信需求。
3.3 基于FIR的数字滤波模块的设计与仿真
在MATLAB中,我们使用Filter函数进行仿真,首先,我们得到成形滤波器的系数为:
0.02122066,0.00773409,-0.03751318,-0.07842133,
-0.05305165,0.07842133,0.28931623,0.48724768,
0.56830989,0.48724768,0.28931623,0.07842133,
-0.05305165,-0.07842133,-0.03751318,0.00773409,
0.02122066;
分别得到如下两路信号:

图3.5 通过FIR滤波器的两路基带信号
I,Q两路基带信号通过成形滤波以后的成形信号。


图3.6 通过FIR滤波器的I,Q两路眼图信号
3.4 基于QPSK的语音信号调制解调模块的设计与仿真
这里,我们对语音信号的QPSK调制解调进行仿真,整个过程为,将抽样量化后的二进制数字信号进行成型滤波,然后进行正交调制,从而获得QPSK中频信号。其MATLAB仿真效果如下图所示:

图3.7QPSK调制信号
其中频信号如下所示:

图3.8 调制后的语音发送信号
QPSK调制解调的MATLAB算法程序如下所示:
%调制
function [I_Data,Q_Data] = QPSK_signal(len);
%QPSK信号源
%I_Data=randint(len,1)*2-1;
%Q_Data=randint(len,1)*2-1;
%s=I_Data + j*Q_Data;
I_Data = randint(len,1)*2-1;
Q_Data = randint(len,1)*2-1;
%解调
n=1000;
x = randint(n,1); %产生信源。
h = modem.pskmod (4); %产生调制句柄
y = modulate(h,x); %对信号进行调制
g = modem.pskdemod (h) %产生解调句柄
z = demodulate(g,y); %进行解调
根据第二章的理解介绍,使用本文所提出的结合VSLMS滤波和子空间滤波的语音降噪算法进行仿真,通过仿真,分别在信噪比在5dB和15dB下进行仿真分析,通过仿真,我们可以得到如下的仿真效果:


图3.9基于VSLMS算法和子空间降噪算法的滤波效果(SNR=5dB,15dB)
下面,我们分别对三种滤波算法前后误差的比较。
我们将最后滤波输出的有效信号和有用元音信号做比较,对信号首先做归一化处理,然后计算输出信号和有用信号的相对误差。从图中可以看出,其最后的误差在10%以内,因此,滤波性能得到了明显的改善。

 举报
举报














 举报
举报

