1、引言
第二代数字卫星广播标准DVB-S2自发布以来一直广受关注,他采用了由BCH外码和LDPC内码级联而成的前向纠错编码(FEC)系统,有效地降低了系统解调门限,几乎可以接近香农限,此外还使用了多种具有高频带利用率的调制方式,大幅度提高了信道传输能力。DVB-S2技术上的突破扩大了他的应用范围,服务范围包括广播业务(BS)、数字新闻采集(DSNG)、数据分配/中继,以及Internet接人等交互式业务。同时新的编码技术使其可以工作在更为恶劣的信道环境中,保证了卫星传输的通信质量。卫星数字电视直播产业已经在全球形成发展热点,随着业务的拓展,数字卫星接收机将具有广阔的市场前景。
DVB-S2的前向纠错系统(FEC)中配合LDPC码使用了长BCH,其码字长度为16 200~58 320 b(正常帧模式)及14 400~3 240 b(缩短帧模式)不等。长BCH码极大地增加了硬件的实现难度,满足芯片面积要求的同时,更要求其译码速度能够符合前级LDPC译码器输出。本文通过对长BCH码优化方法的研究与讨论,针对标准中二进制BCH码的特性,设计了实现该译码器的FPGA硬件结构。
2、BCH编译码原理及算法
BCH码是可以纠正多个随即错误的循环码,可以用生成多项式g(x)来构成,循环码的生成多项式可以表示成g(x)=LCM[g1(x),g2(x),…,gi(x)],其中g1(x),g2(x),…,gi(x)是g(x)零点的最小多项式,LCM表示这些最小多项式的最小公倍式。倘若给定一个BCH码的码长n和纠错能力t,我们可以计算a,a2,a3,…,a2t在GF(q)上的最小多项式gi(x),i=1,2,…,2t(其中a是GF(qm)上的本原域元素),来构成该BCH码的生成多项式:
g(x)=LCM[g1(x),g2(x),…,gi(x)]
BCH码的译码方法主要分两大类:时域译码和频域译码,目前普遍使用的是时域中迭代译码的方法。BCH码的译码过程遵循循环码和线性码的一般译码步骤:
(1)计算接收码字R(x)的伴随S(x);
(2)根据伴随式S(x)找出估计错误图样E(x);
(3)R(x)-E(x)=C1,得到译码器输出的估计值;若C1=C,则译码正确,否则译码错误。
其中对于可纠正t个错误的BCH码而言,需要计算2t个伴随式。由伴随式Sj求出错误位置多项式Λ(x)和错误值多项式ω(x)。这一过程有多种实现算法,常用的有Peterson算法,Berlekamp算法以及Euclid算法。其中Peterson算法需要完成矩阵求逆运算,当纠错数t较小时,该算法有很高的效率,但随着纠错能力t的增加,其运算量迅速增加。对于纠错数t较大的情况下,后两种基于迭代的方法更常用。之后一般利用钱氏搜索算法来计算错误位置多项式Λ(x)的根,即位错误位置X1,X2,…,Xt。该算法实质是一种穷尽法,将每个位置代人多项式验证是否为错误位置,在工程上很好地解决了错误位置求解的问题。同时一般利用Forney算法通过错误位置多项式Λ(x)和错误值多项式ω(x)来计算错误值Y1,Y2,…,Yt。最后由错误位置Xi和错误值Yi得到错误图样E(x),通过R(x)-E(x)=C1纠正错误值,并输出最终译码值。
3、BCH译码器硬件结构
在这一节中,本文将针对DVB-S2中BCH码的特性,提出一种高效、低复杂度的译码器硬件结构。根据译码原理,译码器一般由5个部分组成,如图1所示。
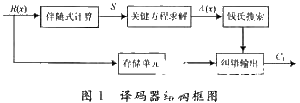
其中R(x)为接收的码字,S为所求的伴随式,Λ(x)为错误位置多项式,C1为输出的译码值。
针对标准中二进制BCH码的特殊性,对各模块作了如下优化:
(1)利用二进制BCH码的特性,减少伴随式的计算数量,以并行结构实现;
(2)采用无逆二进制Berlekamp算法,减少迭代次数,并从算法上去除了错误值多项式ω(x)的求解、求逆运算,省去相应硬件开销;采用序列化硬件结构,复用迦罗华域乘法器数量;
(3)并行结构实现钱氏搜索;
(4)利用递归匹配和群组递归匹配的方法,优化伴随式、钱氏搜索中使用的迦罗华域固定因子乘法器。
3.1 伴随式计算
在BCH译码过程中所需计算的伴随式个数为2t,即可纠正错误数t的2倍。DVB-S2中正常帧长模式下的BCH码分别由(65 535,65 343,12),(65 535,65 375,10)和(65 535,65 407,8)三种码截短而得,可纠正12,10,8个错误,相应需要计算24,20,16个伴随式。伴随式计算公式如下:
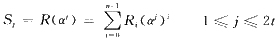
从伴随式的计算公式可知,完成一个伴随式的计算,需要一个码字所有码元输入花费的时间。因此码长为n的情况下,码元逐一输入,计算一个伴随式则需要n个时钟。为了减少伴随式计算时间,采用图2并行结构计算伴随式。一个时钟并行输入P位,则计算一个伴随式只需要[n/P]个时钟。

因此对于DVB-S2中的BCH码,最多只需计算12个伴随式,减少了一半的计算数量。最后由于P位并行输入,寄存器D中的值进入下一次累加之前,需要乘以一个常数api。对于迦罗华域上的固定因子乘法器,可通过递归匹配的方法,消除冗余的公共子项,达到优化的目的。
3.2 关键方程的求解
关键方程的求解有多种适于硬件实现的算法,例如Peterson、Berlekamp-Massey或者Euclid的算法。关键方程的求解主要用于计算错误位置多项式Λ(x)和错误值多项式ω(x),对于DVB-S2中的二进制BCH码,无需计算错误值多项式ω(x),此外还要考虑迦罗华域上求逆、乘法器等大面积的运算单元数量。通过比较,本文选择了针对二进制BCH码改进的无逆Berlekamp算法(inversionless Berlekamp)。
算法描述如下:
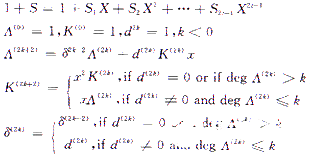
其中d(2k)为(1+S)Λ(2k)乘积项中X(2k+1)的系数,迭代至Ssk+1不存在时,迭代结束,Λ(x)即为所求的错误位置多项式。
首先该算法避免了迦罗华域上的求逆运算,大大简化了电路,同时针对二进制BCH码,简化了迭代算法,所需的迭代步骤减少为原来的一半,因此对于可纠正错误数t=12的BCH码只需迭代12次就可以得到错误位置多项式Λ(x),同时该算法中并未涉及到错误值多项式ω(x)的计算,从算法上去除了错误值多项式的求解,减少了不必要的硬件开销。
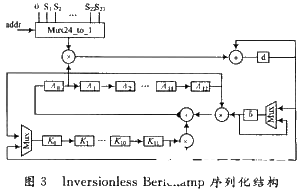
该算法易于硬件实现,但若使用并行结构实现此算法,那么整个关键方程的求解只需12个时钟,但需要38个16位的迦罗华域乘法器。16位的迦罗华域乘法器相当消耗资源,该模块所占的面积由乘法器的数量决定。若采用序列化的结构复用乘法器,虽然增加了一定译码延时,但可将乘法器个数减至3个,大大减少了硬件面积。因此本文采用图3所示序列化的结构,该结构一共只使用了3个16位的迦罗华域乘法器,迭代一次需要14个时钟,迭代次数为可纠正错误数(t次)。当t=12时,最多需要168个时钟。增加了少量译码延时,但大大减少硬件面积,同时所增加的译码延时要远小于一个码字的译码周期,对于整个码字的译码速度影响不是很大。
3.3 钱氏搜索
得到错误位置多项式Λ(x)后,需要求解该方程的根来确定错误位置,钱氏搜索法在工程上很好地解决了对于该方程求根的问题。其本质上是一种穷举法,将可能的错误位置逐一代入方程验证,以确定是否在该位置发生了错误,即验证ai是否为Λ(x)的根:
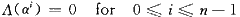
同样的n个可能的位置都需要逐一代人验证,一共需要n个时钟;同伴随式计算一样,为了提高运算速度,本文采用并行结构实现钱氏搜索。

3.4 迦罗华域上固定因子乘法器的优化
在伴随式及钱氏搜索模块中都用到了迦罗华域上的固定因子乘法器,根据文献[1]中描述的Iterative Matc- hing Algorithm(IMA)算法,通过迭代找出公共子项,减少冗余计算单元,以减小电路面积。
算法描述如下:设B为迦罗华域上的变量,C是B与常数ai的乘积;
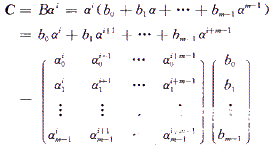
用自然基表示法表示域上的常数,也即用[ai0,ai1,ai2,…,aim-1]来表示ai。由于ai为已知常数,故乘积C的各元素也就是B各元素的加权组合,二进制加法可由异或门来实现,系数矩阵即由a的i~(i+m-1)次方组成。通过迭代匹配的算法,逐次找出系数矩阵中的公共子项,通过最大限度地共享公共项来减少面积。迭代过程分为以下4个步骤:
(1)找出a系数矩阵中各行相匹配的位数;
(2)确定最多匹配的位数;
(3)从匹配的两行中去除冗余部分(匹配部分),并将去除的冗余部分作为一个新行添加到系数矩阵末;
(4)重复执行步骤(1)~(3),直到匹配数《2,寻找匹配时包括新添加的行。
伴随式计算中可以利用该算法,减少固定因子乘法器的面积,对于钱氏搜索模块可以利用群组匹配作进一步的优化,如图4中,P个位置并行验证时,系数Λi需要乘以P个固定常数,可将P个常数以组的形式进行匹配,最大化地消除冗余子项。
4、 仿真结果
用Verilog硬件描述语言完成了BCH码译码器的RTL级设计,用Modelsim进行了功能仿真,并用QuartusII进行了综合。本文提出的结构中,关键方程模块相对独立、固定,伴随式及钱搜索的并行位数取值,应根据整个系统时钟及内码LDPC输出速率综合考虑。仿真设计中采用了15位的并行输入/输出,Modelsim功能仿真波形图如图5所示。

5、 结语
本文针对DVB-B2标准中BCH码的特殊性,提出了一种适合FPGA实现的硬件结构。该结构采用并行方式实现伴随式计算、钱氏搜索,选择针对二进制BCH码的无逆Berlekamp算法,减少了迭代次数,并以序列化的结构实现该算法,将16位迦罗会域乘法器减少至3个,大幅度减少了所占硬件资源。并在伴随式计算及钱氏搜索中使用利用递归匹配和群组递归匹配的方法,对固定因子乘法器作了优化。本文提出者的硬件结构,对BCH译码器各模块都作了一定的优化处理,保证译码速度的前提下,尽可能地减少了芯片面积。
(myoschain)
1、引言
第二代数字卫星广播标准DVB-S2自发布以来一直广受关注,他采用了由BCH外码和LDPC内码级联而成的前向纠错编码(FEC)系统,有效地降低了系统解调门限,几乎可以接近香农限,此外还使用了多种具有高频带利用率的调制方式,大幅度提高了信道传输能力。DVB-S2技术上的突破扩大了他的应用范围,服务范围包括广播业务(BS)、数字新闻采集(DSNG)、数据分配/中继,以及Internet接人等交互式业务。同时新的编码技术使其可以工作在更为恶劣的信道环境中,保证了卫星传输的通信质量。卫星数字电视直播产业已经在全球形成发展热点,随着业务的拓展,数字卫星接收机将具有广阔的市场前景。
DVB-S2的前向纠错系统(FEC)中配合LDPC码使用了长BCH,其码字长度为16 200~58 320 b(正常帧模式)及14 400~3 240 b(缩短帧模式)不等。长BCH码极大地增加了硬件的实现难度,满足芯片面积要求的同时,更要求其译码速度能够符合前级LDPC译码器输出。本文通过对长BCH码优化方法的研究与讨论,针对标准中二进制BCH码的特性,设计了实现该译码器的FPGA硬件结构。
2、BCH编译码原理及算法
BCH码是可以纠正多个随即错误的循环码,可以用生成多项式g(x)来构成,循环码的生成多项式可以表示成g(x)=LCM[g1(x),g2(x),…,gi(x)],其中g1(x),g2(x),…,gi(x)是g(x)零点的最小多项式,LCM表示这些最小多项式的最小公倍式。倘若给定一个BCH码的码长n和纠错能力t,我们可以计算a,a2,a3,…,a2t在GF(q)上的最小多项式gi(x),i=1,2,…,2t(其中a是GF(qm)上的本原域元素),来构成该BCH码的生成多项式:
g(x)=LCM[g1(x),g2(x),…,gi(x)]
BCH码的译码方法主要分两大类:时域译码和频域译码,目前普遍使用的是时域中迭代译码的方法。BCH码的译码过程遵循循环码和线性码的一般译码步骤:
(1)计算接收码字R(x)的伴随S(x);
(2)根据伴随式S(x)找出估计错误图样E(x);
(3)R(x)-E(x)=C1,得到译码器输出的估计值;若C1=C,则译码正确,否则译码错误。
其中对于可纠正t个错误的BCH码而言,需要计算2t个伴随式。由伴随式Sj求出错误位置多项式Λ(x)和错误值多项式ω(x)。这一过程有多种实现算法,常用的有Peterson算法,Berlekamp算法以及Euclid算法。其中Peterson算法需要完成矩阵求逆运算,当纠错数t较小时,该算法有很高的效率,但随着纠错能力t的增加,其运算量迅速增加。对于纠错数t较大的情况下,后两种基于迭代的方法更常用。之后一般利用钱氏搜索算法来计算错误位置多项式Λ(x)的根,即位错误位置X1,X2,…,Xt。该算法实质是一种穷尽法,将每个位置代人多项式验证是否为错误位置,在工程上很好地解决了错误位置求解的问题。同时一般利用Forney算法通过错误位置多项式Λ(x)和错误值多项式ω(x)来计算错误值Y1,Y2,…,Yt。最后由错误位置Xi和错误值Yi得到错误图样E(x),通过R(x)-E(x)=C1纠正错误值,并输出最终译码值。
3、BCH译码器硬件结构
在这一节中,本文将针对DVB-S2中BCH码的特性,提出一种高效、低复杂度的译码器硬件结构。根据译码原理,译码器一般由5个部分组成,如图1所示。

其中R(x)为接收的码字,S为所求的伴随式,Λ(x)为错误位置多项式,C1为输出的译码值。
针对标准中二进制BCH码的特殊性,对各模块作了如下优化:
(1)利用二进制BCH码的特性,减少伴随式的计算数量,以并行结构实现;
(2)采用无逆二进制Berlekamp算法,减少迭代次数,并从算法上去除了错误值多项式ω(x)的求解、求逆运算,省去相应硬件开销;采用序列化硬件结构,复用迦罗华域乘法器数量;
(3)并行结构实现钱氏搜索;
(4)利用递归匹配和群组递归匹配的方法,优化伴随式、钱氏搜索中使用的迦罗华域固定因子乘法器。
3.1 伴随式计算
在BCH译码过程中所需计算的伴随式个数为2t,即可纠正错误数t的2倍。DVB-S2中正常帧长模式下的BCH码分别由(65 535,65 343,12),(65 535,65 375,10)和(65 535,65 407,8)三种码截短而得,可纠正12,10,8个错误,相应需要计算24,20,16个伴随式。伴随式计算公式如下:
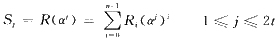
从伴随式的计算公式可知,完成一个伴随式的计算,需要一个码字所有码元输入花费的时间。因此码长为n的情况下,码元逐一输入,计算一个伴随式则需要n个时钟。为了减少伴随式计算时间,采用图2并行结构计算伴随式。一个时钟并行输入P位,则计算一个伴随式只需要[n/P]个时钟。

因此对于DVB-S2中的BCH码,最多只需计算12个伴随式,减少了一半的计算数量。最后由于P位并行输入,寄存器D中的值进入下一次累加之前,需要乘以一个常数api。对于迦罗华域上的固定因子乘法器,可通过递归匹配的方法,消除冗余的公共子项,达到优化的目的。
3.2 关键方程的求解
关键方程的求解有多种适于硬件实现的算法,例如Peterson、Berlekamp-Massey或者Euclid的算法。关键方程的求解主要用于计算错误位置多项式Λ(x)和错误值多项式ω(x),对于DVB-S2中的二进制BCH码,无需计算错误值多项式ω(x),此外还要考虑迦罗华域上求逆、乘法器等大面积的运算单元数量。通过比较,本文选择了针对二进制BCH码改进的无逆Berlekamp算法(inversionless Berlekamp)。
算法描述如下:
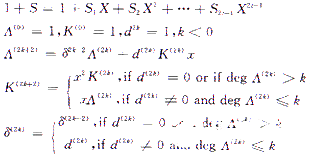
其中d(2k)为(1+S)Λ(2k)乘积项中X(2k+1)的系数,迭代至Ssk+1不存在时,迭代结束,Λ(x)即为所求的错误位置多项式。
首先该算法避免了迦罗华域上的求逆运算,大大简化了电路,同时针对二进制BCH码,简化了迭代算法,所需的迭代步骤减少为原来的一半,因此对于可纠正错误数t=12的BCH码只需迭代12次就可以得到错误位置多项式Λ(x),同时该算法中并未涉及到错误值多项式ω(x)的计算,从算法上去除了错误值多项式的求解,减少了不必要的硬件开销。
该算法易于硬件实现,但若使用并行结构实现此算法,那么整个关键方程的求解只需12个时钟,但需要38个16位的迦罗华域乘法器。16位的迦罗华域乘法器相当消耗资源,该模块所占的面积由乘法器的数量决定。若采用序列化的结构复用乘法器,虽然增加了一定译码延时,但可将乘法器个数减至3个,大大减少了硬件面积。因此本文采用图3所示序列化的结构,该结构一共只使用了3个16位的迦罗华域乘法器,迭代一次需要14个时钟,迭代次数为可纠正错误数(t次)。当t=12时,最多需要168个时钟。增加了少量译码延时,但大大减少硬件面积,同时所增加的译码延时要远小于一个码字的译码周期,对于整个码字的译码速度影响不是很大。

3.3 钱氏搜索
得到错误位置多项式Λ(x)后,需要求解该方程的根来确定错误位置,钱氏搜索法在工程上很好地解决了对于该方程求根的问题。其本质上是一种穷举法,将可能的错误位置逐一代入方程验证,以确定是否在该位置发生了错误,即验证ai是否为Λ(x)的根:
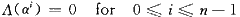
同样的n个可能的位置都需要逐一代人验证,一共需要n个时钟;同伴随式计算一样,为了提高运算速度,本文采用并行结构实现钱氏搜索。

3.4 迦罗华域上固定因子乘法器的优化
在伴随式及钱氏搜索模块中都用到了迦罗华域上的固定因子乘法器,根据文献[1]中描述的Iterative Matc- hing Algorithm(IMA)算法,通过迭代找出公共子项,减少冗余计算单元,以减小电路面积。
算法描述如下:设B为迦罗华域上的变量,C是B与常数ai的乘积;
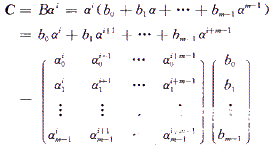
用自然基表示法表示域上的常数,也即用[ai0,ai1,ai2,…,aim-1]来表示ai。由于ai为已知常数,故乘积C的各元素也就是B各元素的加权组合,二进制加法可由异或门来实现,系数矩阵即由a的i~(i+m-1)次方组成。通过迭代匹配的算法,逐次找出系数矩阵中的公共子项,通过最大限度地共享公共项来减少面积。迭代过程分为以下4个步骤:
(1)找出a系数矩阵中各行相匹配的位数;
(2)确定最多匹配的位数;
(3)从匹配的两行中去除冗余部分(匹配部分),并将去除的冗余部分作为一个新行添加到系数矩阵末;
(4)重复执行步骤(1)~(3),直到匹配数《2,寻找匹配时包括新添加的行。
伴随式计算中可以利用该算法,减少固定因子乘法器的面积,对于钱氏搜索模块可以利用群组匹配作进一步的优化,如图4中,P个位置并行验证时,系数Λi需要乘以P个固定常数,可将P个常数以组的形式进行匹配,最大化地消除冗余子项。
4、 仿真结果
用Verilog硬件描述语言完成了BCH码译码器的RTL级设计,用Modelsim进行了功能仿真,并用QuartusII进行了综合。本文提出的结构中,关键方程模块相对独立、固定,伴随式及钱搜索的并行位数取值,应根据整个系统时钟及内码LDPC输出速率综合考虑。仿真设计中采用了15位的并行输入/输出,Modelsim功能仿真波形图如图5所示。

5、 结语
本文针对DVB-B2标准中BCH码的特殊性,提出了一种适合FPGA实现的硬件结构。该结构采用并行方式实现伴随式计算、钱氏搜索,选择针对二进制BCH码的无逆Berlekamp算法,减少了迭代次数,并以序列化的结构实现该算法,将16位迦罗会域乘法器减少至3个,大幅度减少了所占硬件资源。并在伴随式计算及钱氏搜索中使用利用递归匹配和群组递归匹配的方法,对固定因子乘法器作了优化。本文提出者的硬件结构,对BCH译码器各模块都作了一定的优化处理,保证译码速度的前提下,尽可能地减少了芯片面积。
(myoschain)

 举报
举报



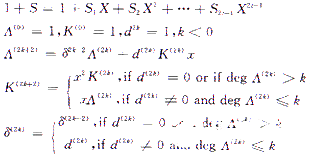


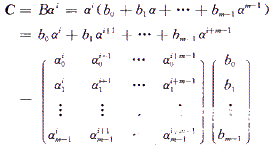


 举报
举报

