1 引言
在许多通信系统中,基站通常会发送训练序列,用于终端和系统取得同步,这里的同步包括时间同步和频率同步,而同步通常包括粗同步和精同步两个步骤。在终端初始接入系统,或者从空闲模式重新接入系统时,通常需要进行粗同步,粗同步的目标是将终端的载波频偏调整到1KHz 以内,粗同步包括频偏估计和频偏调整两个步骤,粗同步通常需要经过若干次的“估计-调整”步骤以达到目标。粗同步完成以后,终端需要进入同步跟踪或精同步阶段。本文考虑频率粗同步过程中的频偏估计算法。
关于频偏估计的文章有很多,如-,文献给出了一种针对UMTS TDD 系统的频偏估计算法,但该算法需要预先计算矩阵的逆,运算复杂度比较大。文献针对LCR-TDD系统,提出一种频率粗同步算法,该算法侧重于同步调整策略,但该算法是针对单径的情况进行分析的。文献在原大唐提出的频偏估计算法的基础上进行了改进,本文是在文献的基础上进行的工作。仿真分析表明,本文的算法比文献更简单,且估计性能更好。为节约篇幅,这里没有给出本文的结果与采用文献的方法得到的结果的对比,详细的对比结果可参见。
2 系统模型

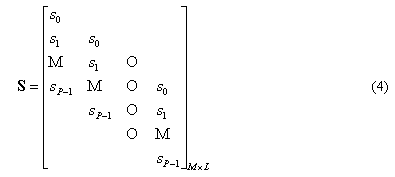
3 频偏估计方法
3.1 最大似然(ML)频偏估计
在单径(即L = 1)情况下,Luise 等人提出一种最大似然频偏估计方法,通过最大化下式
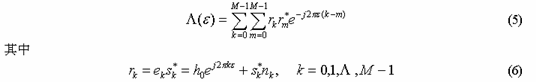
然而,由于式(5)的最大化复杂度很高,无法得到关于频偏估计的闭式表达式,只能通过数值计算。文献在假设载噪比(Carrier-to-Noise-Ratio, CNR)很高,频偏很小的情况下,通过一系列近似,得到以下近似解
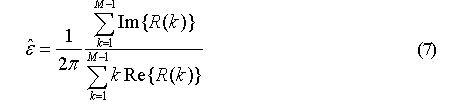
其中, N ≤ M ?1, R(k) 为k r 的自相关函数,定义为
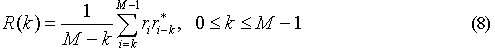
式(7)可以进一步简化为下式
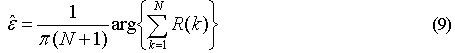
仿真实验表明,在单径的情况下,如果取N = M / 2 ,则利用式(9)得到的频偏估计结果接近Cramer-Rao 下界(CRLB)。
在多径的情况下,最大似然频偏估计可以表示为

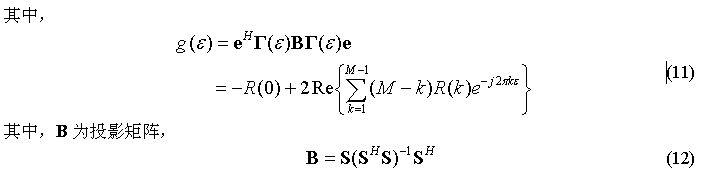
R(k) 为接收信号的加权相关值,
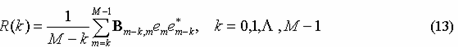
根据式(10)得到频偏估计为无偏估计,且估计方差达到Cramer-Rao 下界。然而,只能通过数值方法进行计算,复杂度很高。
我们利用类似于文献所使用的近似方法,可以得到式(10)在CNR 很高,频偏很小的情况下的近似解
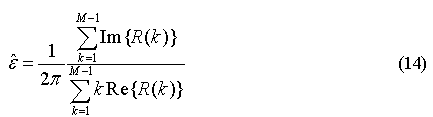
比较式(7)和式(14)可知,两者的形式是完全一致的,只是接收信号的相关值定义不同,在多径的情况下,需要采用投影矩阵B 进行加权,单径只是多径的一种特殊情况而已。为下文表述方便起见,我们将式(14)称为近似最大似然(Approximate Maximum Likelihood, AML)解。
由于AML 只是在高CNR 情况下的近似,因此,在低SNR 的情况下,将变得不适用。而在实际的无线信道中,信道衰落现象使得在某些时刻信噪比变得很低,这时候,AML 得到的频偏估计结果将变得很差。另外,AML 需要存储投影矩阵B,对于不同的信道长度,该矩阵是不同的,针对每种信道长度分别存储一组值将消耗大量的内存。在工程实践中,有必要寻求一种更加简单,更加稳健的频偏估计方法。
3.2 稳健的频偏估计方法
3.2.1 基本原理
从式(1)可以看出,接收到的信号为不同延时的多径信号的组合,每条径对应不同的频偏值。首先需要利用训练序列的良好的自相关特性,分离出各条径。对于对第i 条径,利用训练序列与接收信号进行共轭相关,得到序列
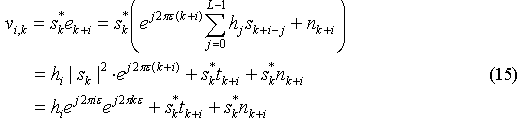
其中上式最后一步利用了训练序列模为1 的特性,
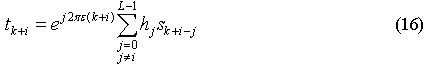

(a) 累加-相关方法
累加-相关方法指的是先将序列i k v , 的前半部分和后半部分分别累加,然后对累加结果进行相关,这里的相关指的是两个值共轭相乘。
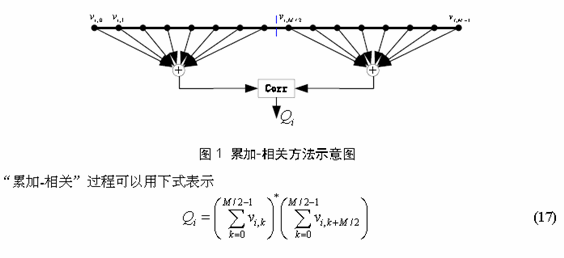
(b) 相关-累加方法
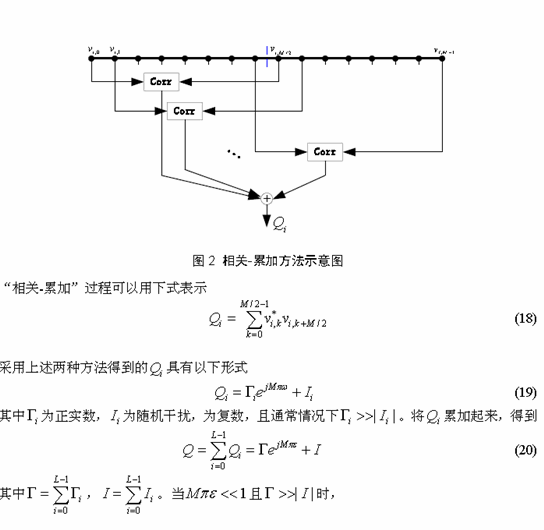
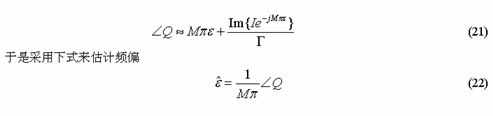
3.2.2 性能分析

(a)累加-相关方法的估计性能


(b) 相关-累加方法的估计性能
将式(25)代入(18)可得


在多径的情况下,由于符号之间的干扰,使得式(28)和式(33)所表示的干扰项还包括不同延时的信号之间的相互干扰项,这使得频偏估计性能分析变得十分困难,为简便起见,我们在分析估计方差时,忽略不同延时的信号之间的干扰项,这样得到的频偏估计方差比真实值要小。对于“累加-相关”法,可以得到

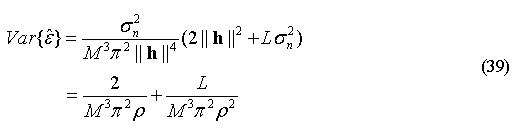
4性能仿真
下面通过仿真实验来对比各种算法的估计性能。采用均方根误差(RMSE)来衡量各种估计算法的性能,其中RMSE 定义如下

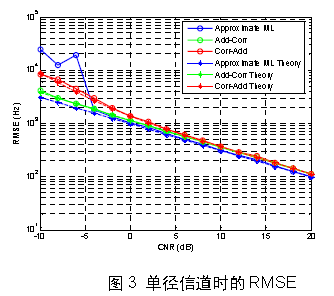
图4 为多径个数L=4,且多径个数准确估计的情况下仿真得到的频偏估计RMSE。在高CNR 区域,AML 具有最佳的性能,“累加-相关”方法与之接近,而“相关-累加”方法性能最差;在低CNR 区域,AML 性能最差,而“累加-相关”方法性能最佳。
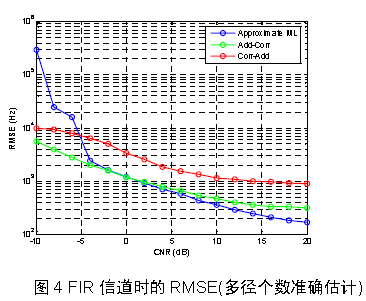
图5 为多径个数L=4,且估计的多径个数为5(多径个数过估计)的情况下仿真得到的频偏估计RMSE。这种情况下,“相关-累加”法和AML 的估计性能比多径个数准确估计时相比,性能略有下降,但“累加-相关”法性能没有下降。
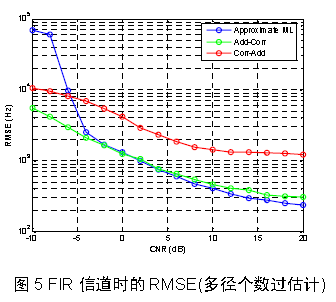
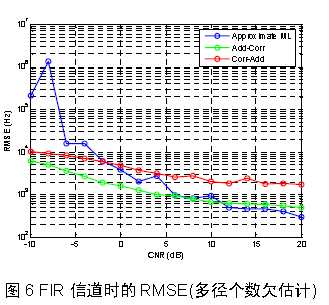
图6 为多径个数L=4,且估计的多径个数为3(多径个数欠估计)的情况下仿真得到的频偏估计RMSE。这种情况下,各种算法的估计性能比多径个数准确估计时相比,性能下降较多。这是因为AML 算法只有在充分利用所有径的情况下才能体现其性能优势,当最后一条径功率较大(相应的,前面的几条径功率总和较小)时,容易出现异常值。而“累加-相关”法和“相关-累加”法则相对稳健一些。
5 结论
本文比较了近似最大似然频偏估计算法,“累加-相关”法和“相关-累加”法的频偏估计性能。仿真结果表明,在高CNR 的情况下,“累加-相关”方法与近似最大似然估计算法的性能接近但前者的计算复杂度和空间复杂度要低许多。另外,在多径个数估计不准,以及在低CNR 的情况下,该方法具有良好的稳健性。综上所述,“累加-相关”频偏估计方法非常适合于工程实现。
1 引言
在许多通信系统中,基站通常会发送训练序列,用于终端和系统取得同步,这里的同步包括时间同步和频率同步,而同步通常包括粗同步和精同步两个步骤。在终端初始接入系统,或者从空闲模式重新接入系统时,通常需要进行粗同步,粗同步的目标是将终端的载波频偏调整到1KHz 以内,粗同步包括频偏估计和频偏调整两个步骤,粗同步通常需要经过若干次的“估计-调整”步骤以达到目标。粗同步完成以后,终端需要进入同步跟踪或精同步阶段。本文考虑频率粗同步过程中的频偏估计算法。
关于频偏估计的文章有很多,如-,文献给出了一种针对UMTS TDD 系统的频偏估计算法,但该算法需要预先计算矩阵的逆,运算复杂度比较大。文献针对LCR-TDD系统,提出一种频率粗同步算法,该算法侧重于同步调整策略,但该算法是针对单径的情况进行分析的。文献在原大唐提出的频偏估计算法的基础上进行了改进,本文是在文献的基础上进行的工作。仿真分析表明,本文的算法比文献更简单,且估计性能更好。为节约篇幅,这里没有给出本文的结果与采用文献的方法得到的结果的对比,详细的对比结果可参见。
2 系统模型

3 频偏估计方法
3.1 最大似然(ML)频偏估计
在单径(即L = 1)情况下,Luise 等人提出一种最大似然频偏估计方法,通过最大化下式
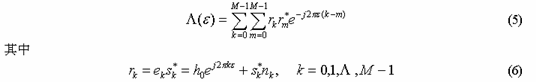
然而,由于式(5)的最大化复杂度很高,无法得到关于频偏估计的闭式表达式,只能通过数值计算。文献在假设载噪比(Carrier-to-Noise-Ratio, CNR)很高,频偏很小的情况下,通过一系列近似,得到以下近似解
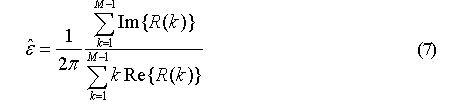
其中, N ≤ M ?1, R(k) 为k r 的自相关函数,定义为
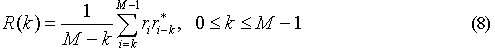
式(7)可以进一步简化为下式
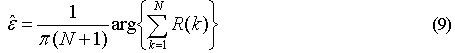
仿真实验表明,在单径的情况下,如果取N = M / 2 ,则利用式(9)得到的频偏估计结果接近Cramer-Rao 下界(CRLB)。
在多径的情况下,最大似然频偏估计可以表示为

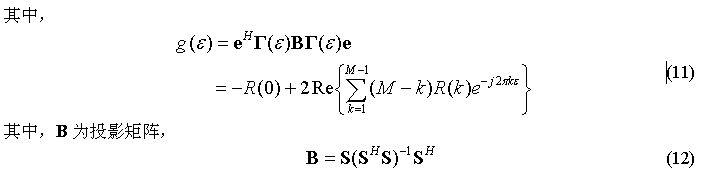
R(k) 为接收信号的加权相关值,
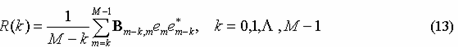
根据式(10)得到频偏估计为无偏估计,且估计方差达到Cramer-Rao 下界。然而,只能通过数值方法进行计算,复杂度很高。
我们利用类似于文献所使用的近似方法,可以得到式(10)在CNR 很高,频偏很小的情况下的近似解
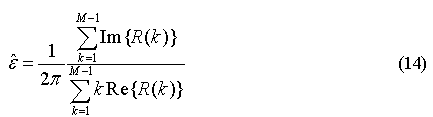
比较式(7)和式(14)可知,两者的形式是完全一致的,只是接收信号的相关值定义不同,在多径的情况下,需要采用投影矩阵B 进行加权,单径只是多径的一种特殊情况而已。为下文表述方便起见,我们将式(14)称为近似最大似然(Approximate Maximum Likelihood, AML)解。
由于AML 只是在高CNR 情况下的近似,因此,在低SNR 的情况下,将变得不适用。而在实际的无线信道中,信道衰落现象使得在某些时刻信噪比变得很低,这时候,AML 得到的频偏估计结果将变得很差。另外,AML 需要存储投影矩阵B,对于不同的信道长度,该矩阵是不同的,针对每种信道长度分别存储一组值将消耗大量的内存。在工程实践中,有必要寻求一种更加简单,更加稳健的频偏估计方法。
3.2 稳健的频偏估计方法
3.2.1 基本原理
从式(1)可以看出,接收到的信号为不同延时的多径信号的组合,每条径对应不同的频偏值。首先需要利用训练序列的良好的自相关特性,分离出各条径。对于对第i 条径,利用训练序列与接收信号进行共轭相关,得到序列
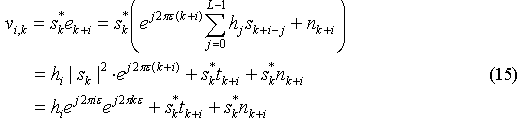
其中上式最后一步利用了训练序列模为1 的特性,
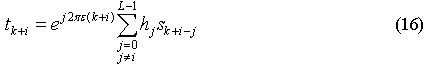

(a) 累加-相关方法
累加-相关方法指的是先将序列i k v , 的前半部分和后半部分分别累加,然后对累加结果进行相关,这里的相关指的是两个值共轭相乘。

(b) 相关-累加方法

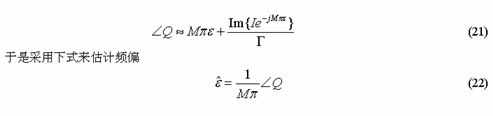
3.2.2 性能分析

(a)累加-相关方法的估计性能


(b) 相关-累加方法的估计性能
将式(25)代入(18)可得


在多径的情况下,由于符号之间的干扰,使得式(28)和式(33)所表示的干扰项还包括不同延时的信号之间的相互干扰项,这使得频偏估计性能分析变得十分困难,为简便起见,我们在分析估计方差时,忽略不同延时的信号之间的干扰项,这样得到的频偏估计方差比真实值要小。对于“累加-相关”法,可以得到

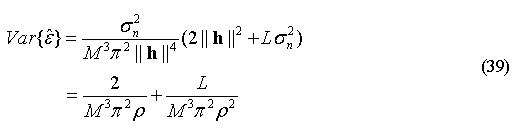
4性能仿真
下面通过仿真实验来对比各种算法的估计性能。采用均方根误差(RMSE)来衡量各种估计算法的性能,其中RMSE 定义如下


图4 为多径个数L=4,且多径个数准确估计的情况下仿真得到的频偏估计RMSE。在高CNR 区域,AML 具有最佳的性能,“累加-相关”方法与之接近,而“相关-累加”方法性能最差;在低CNR 区域,AML 性能最差,而“累加-相关”方法性能最佳。

图5 为多径个数L=4,且估计的多径个数为5(多径个数过估计)的情况下仿真得到的频偏估计RMSE。这种情况下,“相关-累加”法和AML 的估计性能比多径个数准确估计时相比,性能略有下降,但“累加-相关”法性能没有下降。

图6 为多径个数L=4,且估计的多径个数为3(多径个数欠估计)的情况下仿真得到的频偏估计RMSE。这种情况下,各种算法的估计性能比多径个数准确估计时相比,性能下降较多。这是因为AML 算法只有在充分利用所有径的情况下才能体现其性能优势,当最后一条径功率较大(相应的,前面的几条径功率总和较小)时,容易出现异常值。而“累加-相关”法和“相关-累加”法则相对稳健一些。

5 结论
本文比较了近似最大似然频偏估计算法,“累加-相关”法和“相关-累加”法的频偏估计性能。仿真结果表明,在高CNR 的情况下,“累加-相关”方法与近似最大似然估计算法的性能接近但前者的计算复杂度和空间复杂度要低许多。另外,在多径个数估计不准,以及在低CNR 的情况下,该方法具有良好的稳健性。综上所述,“累加-相关”频偏估计方法非常适合于工程实现。

 举报
举报


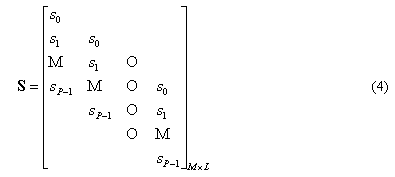
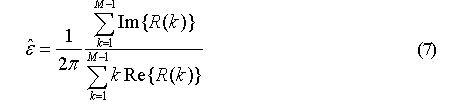
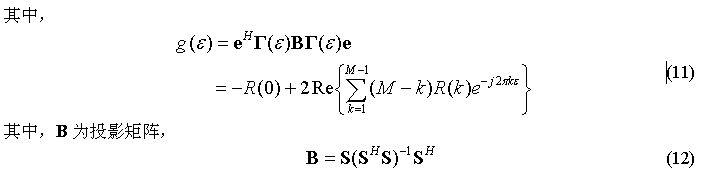
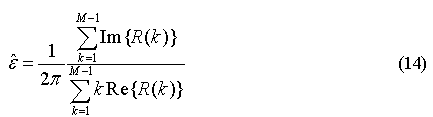
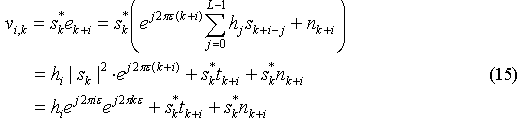


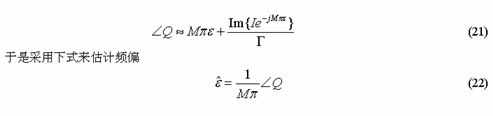









 举报
举报

