Voronoi图是一种空间分割算法。其是对空间中的n 个离散点而言的,它将平面分割为n 个区域,每个区域包括一个点,此区域是到该点距离最近的点的集合。由于Voronoi图具有最邻近性,邻接性等众多性质和完善的理论体系,其被广泛的应用在地理学、气象学、结晶学、航天、机器人等领域。
Voronoi图的生成主要有矢量方法和栅格方法。矢量法中,典型的方法有增量法、分治法和间接法。分治法是一种递归方法,算法思路简单,但是很难在应用过程中实现动态更新。间接法则是根据其对偶图Delaunay三角网来构造Voronoi图,因此其性能的高低由所采用的Delaunay三角网的构造算法所决定。增量法通过不断向已生成的Voronoi图中增加点来动态构建Voronoi图。相对于前两种方法,增量法构造简单并且容易实现动态化,所以被广泛应用。矢量方法的优势是生成Voronoi图精度高,但是存在存储复杂,生长元只能是点和线,以及难以向三维及高维空间扩展等问题。因此本文重点研究了Voronoi图的栅格生成方法,首先比较了常见的栅格方法生成Voronoi图的优缺点,然后结合CUDA的出现,提出一种基于GPU的Voronoi图并行栅格生成算法。
1 栅格法简介
栅格方法生成Voronoi图主要是将二值图像转化为栅格图像,然后确定各个空白栅格归属。主要方法有两类,一类以空白栅格为中心,计算每个空白栅格到生长目标的距离,以确定其归属,常见的方法有代数距离变换法,逐个空白栅格确定法等;另一类以生长目标为中心,不断扩张生长目标的距离半径,填充其中的空白栅格,直到将整个图像填充完成,主要有圆扩张法,数学形态学距离变换法等。代数距离变换法对距离图像进行上行扫描(从上到下,从左到右)和下行扫描(从下向上,从右到左)两次扫描,计算出每个空白栅格最邻近的生长目标,以此生长目标作为其归属。此方法中栅格距离的定义直接影响了空白栅格的归属和Voronoi图的生成精度,通常使用的栅格距离定义有街区距离、八角形距离、棋盘距离等。距离变换的栅格生成方法精度低、耗时长,所需要花费的时间和栅格的数量成正比,当栅格为n×n 大小时,其时间复杂度为O(n×n)。圆检测法以生长目标为圆心,以一定的步长为初始半径,所有生长目标同时对其构成的圆内的空白栅格进行覆盖。通过不断扩大生长目标的半径,将会有越来越多的空白栅格被各个圆所覆盖,直到最终覆盖完整个图像。数学形态学距离变换法与圆检测法类似,其思想来源于数学形态学中膨胀操作,膨胀操作起到了扩大图像的效果,通过不断的对生长目标进行膨胀操作,最终扩张到所有的空白栅格。这两种方法有个共同的缺点,在每次扩张后,都需要判断整个栅格图像是否已完成扩张,而这需要遍历栅格图像,十分耗时。
2 GPU下的栅格生成方法
2.1 CUDA编程模型与GPU
CUDA是一个并行编程模型和一个软件编程环境,其采用了C语言作为编程语言,提供了大量的高性能计算指令开发能力,使开发者能够在GPU的强大计算能力上建立起一种更加高效的密集数据计算解决方案。
CUDA将CPU作为主机端,GPU作为设备端,一个主机端可以有多个设备端。其采用CPU和GPU协同工作的方式,CPU 主要负责程序中的串行计算的部分,GPU主要负责程序中的并行计算的部分。GPU上运行的代码被称为内核函数,其能够被GPU上内置的多个线程并行执行。一个完整的任务处理程序由CPU端串行处理代码和GPU端并行内核函数共同构成。当CPU中执行到GPU代码时,其首先将相关数据复制到GPU中,然后调用GPU的内核函数,GPU中多个线程并行执行此内核函数,当完成计算后,GPU端再把计算的结果返回给CPU,程序继续执行。通过将程序中耗时的且便于并行处理的计算转移到GPU中使用GPU并行处理,以提高整个程序的运行速度。CUDA 是以线程网格(Grid),线程块(Block),线程(Thread)为三层的组织架构,每一个网格由多个线程块构成,而一个线程块又由多个线程构成,如图1所示。在GPU中,线程是并行运行的最小单元,由此可见,当存在大量的线程时,程序的并行程度将会十分高。目前的GPU上一个网格最多包含65535×65535 个线程块,而一个线程块通常有512 个或1024 个线程,所以理论上可以对65535×65535×512个栅格同时进行计算。
2.2 并行Voronoi图栅格生成算法
传统的栅格生成算法中,不论是采用以空白栅格为中心确定其归属的方法,还是以生长目标为中心通过不断增长生长目标半径对空白栅格进行覆盖的方法,他们在计算每个空白栅格距离时,只能通过遍历栅格,逐一处理。而栅格处理过程中的一个重要特点是,各个栅格的计算并不依赖于其他栅格的计算结果。即各个栅格的计算是相互独立的,而由于CPU的串行性,导致了各个栅格只能顺序处理,降低了处理速度。
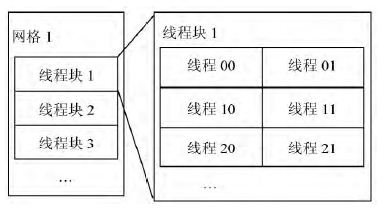
图1 GPU组织架构
由于GPU下的多个线程都是硬件实现的,各个线程的处理都是并行的,因此将栅格距离的计算分散到GPU端各个线程,必然能够提高其生成速度。为了并行处理栅格化图像,可以采用如下的想法,将每一个栅格点对应于一个线程,此线程计算此栅格到所有的生长目标的距离,取最小距离的生长目标作为其归属。即采用一个线程用来确定一个空白栅格归属的方法。
确定方法后,就需要对GPU端内核函数进行设计,由于内核函数是并行处理的执行单元,其设计方式直接决定了GPU端的程序运行效率。因此如何设计良好的内核函数是提高并行速度的关键。本文采用如下方式进行内核函数的设计,假设共分配了K 个并行处理线程,栅格规模为M×N,设A[ i]为第i 个线程处理的栅格编号。当K<M×N 时,只需要将栅格与线程按序依次分配,即第i个线程处理第i个栅格(式(1))即可。当线程个数少于栅格个数时,一个线程必须负责处理多个栅格。首先可以计算出每个线程平均需要处理的栅格个数C=M × N K ,然后对栅格采用具体的分配方式,可以有两种分配方式,一种将连续的C 个栅格分配给一个线程处理,即第i 个线程处理第i×C,i×C+1,i×C+2,…,i×C+C-1个栅格(式(2))。另一种方式为将栅格按C大小分块,将每块的第i 个栅格分配给第i 个线程,即第i 个线程处理第i,C+i,2×C+i,3×C+i,…,(C-1)×C+i 个栅格(式(3))。
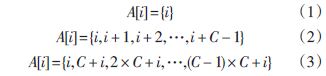
由于显卡上的内存是动态随机存储(DRAM),因此最有效率的存取方式,是以连续的方式存取。当采用第一种方式时,看似是一种连续的存取方式,实际上恰好是非连续的,当第i 个线程处理第i 个栅格时,由于处理需要一定的时间,此时GPU自动将下个一线程i+1需要的内存数据取出给其使用,此时下一个线程的内存数据却是在i+C 处,内存变成了间断存取。而在使用第二种方式进行处理时,恰好是一种连续的存取方式,由于第i 个线程正在处理第i 个栅格数据,此时GPU为第i+1个线程准备数据,而此时的数据正好为第i+1内存处。满足了内存的连续存取特性。因此本文采用第二种方式,内核函数的设计伪代码如下:

具体步骤如下:(这里假设栅格的规模为M×N):
Step1:根据栅格图像的规模,确定GPU端线程块和线程的分配方式和分配数量,初始化GPU端的参数。
Step2:程序调用GPU端内核函数,同时将待处理栅格图像数据传入GPU中。数据主要是图像的栅格距离,一般是二维数组,0表示空白栅格,其他各生长目标可由1,2等不同的数字定义。
Step3:GPU分配M×N 个thread对栅格进行处理,当M×N 大于所有的thread的总数时,可以将M×N 个栅格分块处理,即将其分成A 行×B 列×C 块,其中A×B 小于thread的总数。对于分成了C 块的栅格来说,每个线程只需要处理C 个栅格。
Step4:当生长目标数目不多时,每一个线程计算其对应的栅格到所有的生长目标点的距离,取距离最小的生长目标,为此线程对应的空白栅格的归属,转Step6。当生长目标过多时,则转Step5。
Step5:当生长目标较多时,为了减少遍历生长目标的时间,通过借鉴王新生的算法,不计算栅格点到每一个生长目标的距离,通过对空白栅格不断的进行邻域扩张,直到遇到目标生长点的方法确定此栅格的归属。
Step6 将生成后的数据返回CPU端,CPU端完成栅格图像的显示与后处理。
3 实验与总结
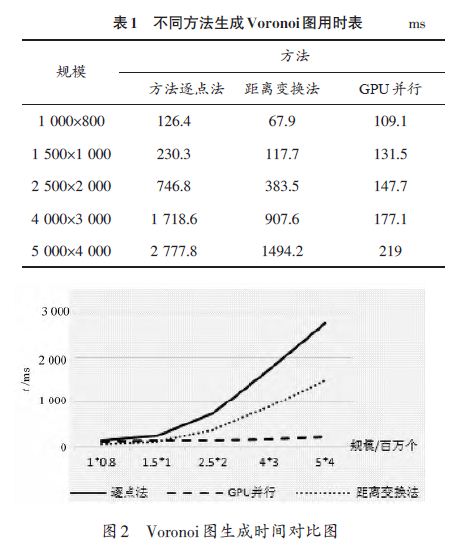
在CPU参数为Intel Xeon CPU E5-2609,2.4 GHz,2 处理器8 核心,GPU 参数为TeslaC2075,448CUDA 核心,显存5.25 GB的试验平台下,做了不同方法在不同栅格规模下生成Voronoi图的对比试验,试验中生长目标的个数定义为100个。由于不同的方法都采用了相同的距离定义,因此各种方法的Voronoi图生成结果都是相同的,即他们之间的生成精度是相同的,所以这里重点比较了不同方法的生成耗时。表1列出了不同方法生成Voronoi图的用时,图2为表1的折线图,从图2中可以明显看出,当栅格数量较少时,GPU并行技术的使用并不能提升生成速度,但是当栅格点数量增加时,逐点法和距离变换法用时明显增加,但GPU并行算法用时几乎不变。
4 结语
通过实验结果可以看出,采用GPU对Voronoi图的生成进行并行加速,能够很好的提高生成速度。其生成Voronoi图所需时间与只与生长目标的数量有关,而与栅格规模没有关系,当生长目标数量为n 时,其时间复杂度近似于O(n),为线性的生成时间。相对于前面的几种CPU下串行算法,尤其是在栅格规模过大的情况下,能够很好的提高Voronoi图的生成速度。
Voronoi图是一种空间分割算法。其是对空间中的n 个离散点而言的,它将平面分割为n 个区域,每个区域包括一个点,此区域是到该点距离最近的点的集合。由于Voronoi图具有最邻近性,邻接性等众多性质和完善的理论体系,其被广泛的应用在地理学、气象学、结晶学、航天、机器人等领域。
Voronoi图的生成主要有矢量方法和栅格方法。矢量法中,典型的方法有增量法、分治法和间接法。分治法是一种递归方法,算法思路简单,但是很难在应用过程中实现动态更新。间接法则是根据其对偶图Delaunay三角网来构造Voronoi图,因此其性能的高低由所采用的Delaunay三角网的构造算法所决定。增量法通过不断向已生成的Voronoi图中增加点来动态构建Voronoi图。相对于前两种方法,增量法构造简单并且容易实现动态化,所以被广泛应用。矢量方法的优势是生成Voronoi图精度高,但是存在存储复杂,生长元只能是点和线,以及难以向三维及高维空间扩展等问题。因此本文重点研究了Voronoi图的栅格生成方法,首先比较了常见的栅格方法生成Voronoi图的优缺点,然后结合CUDA的出现,提出一种基于GPU的Voronoi图并行栅格生成算法。
1 栅格法简介
栅格方法生成Voronoi图主要是将二值图像转化为栅格图像,然后确定各个空白栅格归属。主要方法有两类,一类以空白栅格为中心,计算每个空白栅格到生长目标的距离,以确定其归属,常见的方法有代数距离变换法,逐个空白栅格确定法等;另一类以生长目标为中心,不断扩张生长目标的距离半径,填充其中的空白栅格,直到将整个图像填充完成,主要有圆扩张法,数学形态学距离变换法等。代数距离变换法对距离图像进行上行扫描(从上到下,从左到右)和下行扫描(从下向上,从右到左)两次扫描,计算出每个空白栅格最邻近的生长目标,以此生长目标作为其归属。此方法中栅格距离的定义直接影响了空白栅格的归属和Voronoi图的生成精度,通常使用的栅格距离定义有街区距离、八角形距离、棋盘距离等。距离变换的栅格生成方法精度低、耗时长,所需要花费的时间和栅格的数量成正比,当栅格为n×n 大小时,其时间复杂度为O(n×n)。圆检测法以生长目标为圆心,以一定的步长为初始半径,所有生长目标同时对其构成的圆内的空白栅格进行覆盖。通过不断扩大生长目标的半径,将会有越来越多的空白栅格被各个圆所覆盖,直到最终覆盖完整个图像。数学形态学距离变换法与圆检测法类似,其思想来源于数学形态学中膨胀操作,膨胀操作起到了扩大图像的效果,通过不断的对生长目标进行膨胀操作,最终扩张到所有的空白栅格。这两种方法有个共同的缺点,在每次扩张后,都需要判断整个栅格图像是否已完成扩张,而这需要遍历栅格图像,十分耗时。
2 GPU下的栅格生成方法
2.1 CUDA编程模型与GPU
CUDA是一个并行编程模型和一个软件编程环境,其采用了C语言作为编程语言,提供了大量的高性能计算指令开发能力,使开发者能够在GPU的强大计算能力上建立起一种更加高效的密集数据计算解决方案。
CUDA将CPU作为主机端,GPU作为设备端,一个主机端可以有多个设备端。其采用CPU和GPU协同工作的方式,CPU 主要负责程序中的串行计算的部分,GPU主要负责程序中的并行计算的部分。GPU上运行的代码被称为内核函数,其能够被GPU上内置的多个线程并行执行。一个完整的任务处理程序由CPU端串行处理代码和GPU端并行内核函数共同构成。当CPU中执行到GPU代码时,其首先将相关数据复制到GPU中,然后调用GPU的内核函数,GPU中多个线程并行执行此内核函数,当完成计算后,GPU端再把计算的结果返回给CPU,程序继续执行。通过将程序中耗时的且便于并行处理的计算转移到GPU中使用GPU并行处理,以提高整个程序的运行速度。CUDA 是以线程网格(Grid),线程块(Block),线程(Thread)为三层的组织架构,每一个网格由多个线程块构成,而一个线程块又由多个线程构成,如图1所示。在GPU中,线程是并行运行的最小单元,由此可见,当存在大量的线程时,程序的并行程度将会十分高。目前的GPU上一个网格最多包含65535×65535 个线程块,而一个线程块通常有512 个或1024 个线程,所以理论上可以对65535×65535×512个栅格同时进行计算。
2.2 并行Voronoi图栅格生成算法
传统的栅格生成算法中,不论是采用以空白栅格为中心确定其归属的方法,还是以生长目标为中心通过不断增长生长目标半径对空白栅格进行覆盖的方法,他们在计算每个空白栅格距离时,只能通过遍历栅格,逐一处理。而栅格处理过程中的一个重要特点是,各个栅格的计算并不依赖于其他栅格的计算结果。即各个栅格的计算是相互独立的,而由于CPU的串行性,导致了各个栅格只能顺序处理,降低了处理速度。

图1 GPU组织架构
由于GPU下的多个线程都是硬件实现的,各个线程的处理都是并行的,因此将栅格距离的计算分散到GPU端各个线程,必然能够提高其生成速度。为了并行处理栅格化图像,可以采用如下的想法,将每一个栅格点对应于一个线程,此线程计算此栅格到所有的生长目标的距离,取最小距离的生长目标作为其归属。即采用一个线程用来确定一个空白栅格归属的方法。
确定方法后,就需要对GPU端内核函数进行设计,由于内核函数是并行处理的执行单元,其设计方式直接决定了GPU端的程序运行效率。因此如何设计良好的内核函数是提高并行速度的关键。本文采用如下方式进行内核函数的设计,假设共分配了K 个并行处理线程,栅格规模为M×N,设A[ i]为第i 个线程处理的栅格编号。当K<M×N 时,只需要将栅格与线程按序依次分配,即第i个线程处理第i个栅格(式(1))即可。当线程个数少于栅格个数时,一个线程必须负责处理多个栅格。首先可以计算出每个线程平均需要处理的栅格个数C=M × N K ,然后对栅格采用具体的分配方式,可以有两种分配方式,一种将连续的C 个栅格分配给一个线程处理,即第i 个线程处理第i×C,i×C+1,i×C+2,…,i×C+C-1个栅格(式(2))。另一种方式为将栅格按C大小分块,将每块的第i 个栅格分配给第i 个线程,即第i 个线程处理第i,C+i,2×C+i,3×C+i,…,(C-1)×C+i 个栅格(式(3))。
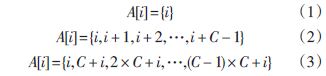
由于显卡上的内存是动态随机存储(DRAM),因此最有效率的存取方式,是以连续的方式存取。当采用第一种方式时,看似是一种连续的存取方式,实际上恰好是非连续的,当第i 个线程处理第i 个栅格时,由于处理需要一定的时间,此时GPU自动将下个一线程i+1需要的内存数据取出给其使用,此时下一个线程的内存数据却是在i+C 处,内存变成了间断存取。而在使用第二种方式进行处理时,恰好是一种连续的存取方式,由于第i 个线程正在处理第i 个栅格数据,此时GPU为第i+1个线程准备数据,而此时的数据正好为第i+1内存处。满足了内存的连续存取特性。因此本文采用第二种方式,内核函数的设计伪代码如下:

具体步骤如下:(这里假设栅格的规模为M×N):
Step1:根据栅格图像的规模,确定GPU端线程块和线程的分配方式和分配数量,初始化GPU端的参数。
Step2:程序调用GPU端内核函数,同时将待处理栅格图像数据传入GPU中。数据主要是图像的栅格距离,一般是二维数组,0表示空白栅格,其他各生长目标可由1,2等不同的数字定义。
Step3:GPU分配M×N 个thread对栅格进行处理,当M×N 大于所有的thread的总数时,可以将M×N 个栅格分块处理,即将其分成A 行×B 列×C 块,其中A×B 小于thread的总数。对于分成了C 块的栅格来说,每个线程只需要处理C 个栅格。
Step4:当生长目标数目不多时,每一个线程计算其对应的栅格到所有的生长目标点的距离,取距离最小的生长目标,为此线程对应的空白栅格的归属,转Step6。当生长目标过多时,则转Step5。
Step5:当生长目标较多时,为了减少遍历生长目标的时间,通过借鉴王新生的算法,不计算栅格点到每一个生长目标的距离,通过对空白栅格不断的进行邻域扩张,直到遇到目标生长点的方法确定此栅格的归属。
Step6 将生成后的数据返回CPU端,CPU端完成栅格图像的显示与后处理。
3 实验与总结
在CPU参数为Intel Xeon CPU E5-2609,2.4 GHz,2 处理器8 核心,GPU 参数为TeslaC2075,448CUDA 核心,显存5.25 GB的试验平台下,做了不同方法在不同栅格规模下生成Voronoi图的对比试验,试验中生长目标的个数定义为100个。由于不同的方法都采用了相同的距离定义,因此各种方法的Voronoi图生成结果都是相同的,即他们之间的生成精度是相同的,所以这里重点比较了不同方法的生成耗时。表1列出了不同方法生成Voronoi图的用时,图2为表1的折线图,从图2中可以明显看出,当栅格数量较少时,GPU并行技术的使用并不能提升生成速度,但是当栅格点数量增加时,逐点法和距离变换法用时明显增加,但GPU并行算法用时几乎不变。

4 结语
通过实验结果可以看出,采用GPU对Voronoi图的生成进行并行加速,能够很好的提高生成速度。其生成Voronoi图所需时间与只与生长目标的数量有关,而与栅格规模没有关系,当生长目标数量为n 时,其时间复杂度近似于O(n),为线性的生成时间。相对于前面的几种CPU下串行算法,尤其是在栅格规模过大的情况下,能够很好的提高Voronoi图的生成速度。

 举报
举报


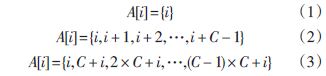



 举报
举报

