欠采样或违反奈奎斯特(nyquist)准则是 ADC 应用上经常使用的一种技术。射频(RF)通信和诸如示波器等高性能测试设备就是其中的一些实例。在这个“灰色”地带中经常出现一些困惑,如是否有必要服从 nyquist 准则,以获取一个信号的内容。本文描述了欠采样的过程,以及它在某些应用中的好处,譬如手机基站和直接 RF 下变频接收器等。选择的这几个实例都采用了美国国家半导体的 ADC。对于 Nyquist 和 Shannon 定理的检验将证明:ADC 采样频率的选择与最大输入信号频率对输入信号带宽的比率有很强的相关性。
Nyquist 和 Shannon 信息定理
Nyquist 定理:nyquist 定理被表达成各种各样的形式,它的原意是:如果要从相等时间间隔取得的采样点中,毫无失真地重建模拟信号波形,则采样频率必须大于或等于模拟信号中最高频率成份的两倍。
因而对于一个最大信号频率为 fMAX 的模拟信号 fa,其最小采样频率 fs 必须大于或等于 2*fMAX 。
Fs ³ 2 f MAX
最简单的模拟信号形式是正弦波,此时所有的信号能量都集中在一个频率上。现实中,模拟信号通常具有复杂的信号波形,并带有众多频率成份或谐波。例如,一个方波除了它的基频之外,还包含有无穷多的奇次谐波。因此,根据 Nyquist 定理,要从时间交叉的采样中完整地重建一个方波,采样频率必须远远高于方波的基频。
请注意:当以采样率 fs 对模拟信号 fa 进行采样时,实际上产生了两个混叠成份,一个位于 fs+ fa,另一个位于 fs-fa。它的频率域显示在图 1中。
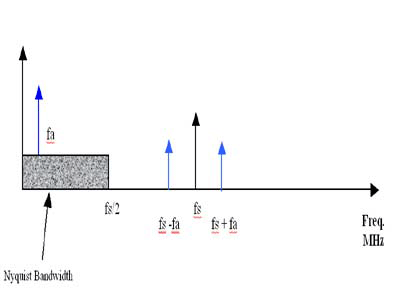
图 1
较高频的混叠成份基本上不会引起问题,因为它位于 nyquist 带宽(fs/2)以外。较低频的混叠成份则可能产生问题,因为它可能落在 nyquist 带宽之内,破坏所需要的信号。鉴于采样系统的混叠现象,nyquist 准则要求采样率 fs 》 fa,以避免混叠成份覆盖到第一 nyquist 区。为防止有害的干扰, 任何落在感兴趣的带宽之外的信号(无论是寄生信号或是随机噪声)都应该在抽样之前进行过滤。这就解释了众多采样系统中,加装抗混叠滤波器的必要性。然而,在下面关于次采样的部分中,会表明存在着一些方法,它们可以在信号处理应用中用到混叠现象的益处。
举例来说:对一个最大频率为 10MHz 信号,为了从采样中不失真地重建模拟信号,nyquist 规定采样频率 ³ 20MSPS (每秒百万次抽样)。
但是,我们很快能看出 nyquist 定理的局限性。Nyquist 假定所需的信息带宽等于 nyquist 带宽或采样频率的一半。在图 1 所示的范例中,如果模拟信号 fa 带宽小于 fs/2,那么有可能用低于 nyquist 率进行采样,仍然能够防止混叠现象的产生,并避免损坏所需的信号。应该观察到,所需最小采样频率实际上是输入信号带宽的一个函数,而不仅取决于最大频率成份。Shannon 定理进一步验证了这一结论。
Shannon 信息定理:
一个带宽为 fb 的模拟信号,采样速率必须为 fs 》 2fb,才能避免信息的损失。信号带宽可以从 DC 到 fb(基带采样),或从 f1 到 f2,其中 fb = f2–f1(欠采样)。因此,Shannon 定理表示:实际所需最小采样频率是信号带宽的函数,而不仅取决于它的最大频率成份。通常来说,采样频率至少必须是信号带宽的两倍,并且被采样的信号不能是 fs/2 的整数倍,以防止混叠成份的相互重叠。注意,fMAX(模拟信号的最大频率成份)对于信号带宽 B 的大比例最小采样频率接近 2B。
在许多应用中,这大大地减少了对 ADC 的要求。对一个具有150MHz最大信号频率,但只有10MHz 带宽的信号进行采样,可能只需要一个约 22MSPS 的ADC,而不是 nyquist 规定的 》 300MSPS 的 ADC。
例如,考虑一个带宽为 10MHz、位于 160 –170MHz 频谱范围内的信号。假定按照 Shannon 定理要 30MSPS 的采样率。由于采样过程会产生附带的采样频率,它们是 30MHz 的整数倍,也就是 60MHz(2fs)、90MHz (3fs)。 180MHz 等。介于 160MHz 和 170MHz 之间的所需信号,在这些采样频率的每个谐波(fs、2fs、3fs等)附近都产生混叠。注意:任何一个混叠成份都是原始信号的一个准确表述。30MSPS 采样使得 160–170MHz 的信号被 折返到 0 -10MHz 的第一 nyquist 区。
从本例中还可注意到:可能存在于 ADC 输出 FFT 中的最高频率成份小于或等于采样频率的一半。或者说,由于谐波折返或欠采样,每一个位于 nyquist 带宽之外的 ADC 输入频率成份总被折返到第一 nyquist 区。这可由下列等式表示。而次采样在实用电子系统有许多用途。最常见的欠采样应用是在数字接收器中。首先让我们更详细地解释次抽样的过程。
次抽样或折返的过程可以看作是 ADC 输入信号与采样频率和其谐波的混合。这意味着,许多频率可以混合为 DC,而不再能确认它们的原始频率。举一个 66MSPS 采样频率的例子,则所有输入信号(66–6、66+6、126、136MHz 等等)频率混合为 6MHz,见图 2。每个采样映象折返到 《 FS/2。请注意,图 2 虚线处将发生相位翻转,但这些成份可在软件中去除。如果必须在 ADC 输出处确定原始的输入频率,则无法使用次采样。因为这违反了 nyquist 准则。如果在 ADC 输出处无需确定载波频率,次采样仍然证明有效。这适用于许多通信系统,如手机基站接收器,因为接收器只需恢复载波上的信息,而不是载波本身。我们以一个常见的数字接收器系统为例。
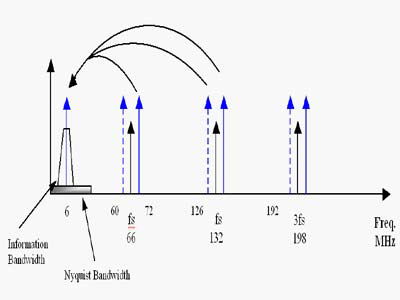
图 2:
射频数字接收器
以使用一个射频载波频率 900MHz(欧洲)和 1800MHz(美国)的 GSM/EDGE 基站为例。一个移动基站接收电路类似图 3 所示。高频射频载波信号首先在混频器和本振级下变频为一个范围 150-190MHz 的中频,供模拟-数字的转换使用。前述 Shannon 定理显示,所必需的采样频率是信号带宽的函数,在 GSM/EDGE 系统中带宽为 200kHz。GSM 系统的动态范围规格需要最小 10 位精度的 ADC,虽然实际都使用 12 位精度。市面上有大量的高速 ADC 可供选择,数字接收器的系统设计师选择器件时必须考虑系统动态范围要求以及器件的成本。由于这些原因,对于 GSM 接收器应用,50-70MSPS 采样率的 ADC 是最常见的选择。虽然在 66MSPS 时 150 –190 兆赫信号为欠采样(使用美国国家半导体的 ADC12DL066, 双 12 位 66MSPS ADC),对于需要的 200kHz 信息带宽,并没有违反 Nyquist 准则。这种选择为 200kHz 的带宽信息信号提供了足够大的空间,同时提供了超过 20dB 的处理增益(下文解释)。请注意,由于种种原因,继续增加采样频率来不断提高处理增益的方法是不切实际的。市面上有更高采样率的 12 位 ADC,譬如 12 位 80MSPS 的 ADC(美国国家半导体 ADC12L080),以及一些 》100MSPS 的 12 位专用 ADC,但低于 100MSPS 和高于 100MSPS 采样率 ADC 之间的成本差别相当大。
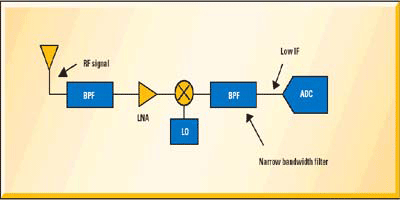
图 3: Edge 中常用的接收器
处理增益
ADC 噪声特性通常由热噪声所限制,当选定 ADC 时,其噪声带宽通常被定义作 nyquist 带宽。在 FS = 66MSPS 时,总噪声底限的测量表示为相对于某一输入信号频率处一个 33MHz 带宽内全量程(dBFS)的 dB 值。对于 ADC12L066,150MHz 输入信号频率时的总噪声底限是 –62dBFS。但是对 ADC输出进行过滤后,会产生一个更窄的带宽,例如美国国家半导体的数字式下变频器 CLC5903。滤波过程提供的噪声处理增益是带宽减少量的函数。200kHz 的信道滤波器可获得如下的处理增益:
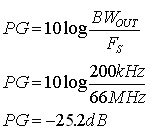
上式假设 ADC 输出的滤波器去除了混叠映象和 Fs 附近的噪声。
这样,200kHz 带宽内的 ADC 输出噪声变成:
62dBFS + (-25.2dB ) = -87.2dBFS。

图 4
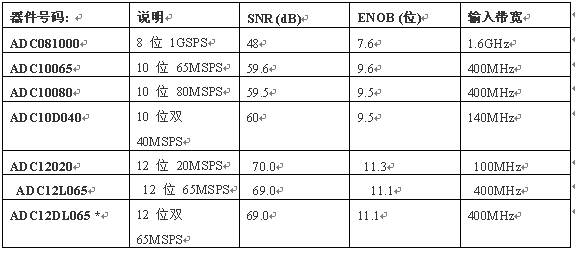
表1 重点列出美国国家半导体的几个最新高速 ADC,它们都适用于欠采样应用。对于这些应用,最重要的参数是模拟输入信号带宽、信噪比(SNR),以及有效位数(ENOB)。
总结
当为某个应用选择正确采样率的 ADC 时,不光要知道最高模拟转换频率这一个参数。Shannon 定理显示,信号带宽同等重要。我们发现,高于 Shannon 速率的采样还有其它的好处,如处理增益可以极大地改善动态范围。系统设计师掌握了这一知识,就能在通用且价格合理的标准 ADC 中,正确地选择 ADC 采样频率和精度。
欠采样或违反奈奎斯特(nyquist)准则是 ADC 应用上经常使用的一种技术。射频(RF)通信和诸如示波器等高性能测试设备就是其中的一些实例。在这个“灰色”地带中经常出现一些困惑,如是否有必要服从 nyquist 准则,以获取一个信号的内容。本文描述了欠采样的过程,以及它在某些应用中的好处,譬如手机基站和直接 RF 下变频接收器等。选择的这几个实例都采用了美国国家半导体的 ADC。对于 Nyquist 和 Shannon 定理的检验将证明:ADC 采样频率的选择与最大输入信号频率对输入信号带宽的比率有很强的相关性。
Nyquist 和 Shannon 信息定理
Nyquist 定理:nyquist 定理被表达成各种各样的形式,它的原意是:如果要从相等时间间隔取得的采样点中,毫无失真地重建模拟信号波形,则采样频率必须大于或等于模拟信号中最高频率成份的两倍。
因而对于一个最大信号频率为 fMAX 的模拟信号 fa,其最小采样频率 fs 必须大于或等于 2*fMAX 。
Fs ³ 2 f MAX
最简单的模拟信号形式是正弦波,此时所有的信号能量都集中在一个频率上。现实中,模拟信号通常具有复杂的信号波形,并带有众多频率成份或谐波。例如,一个方波除了它的基频之外,还包含有无穷多的奇次谐波。因此,根据 Nyquist 定理,要从时间交叉的采样中完整地重建一个方波,采样频率必须远远高于方波的基频。
请注意:当以采样率 fs 对模拟信号 fa 进行采样时,实际上产生了两个混叠成份,一个位于 fs+ fa,另一个位于 fs-fa。它的频率域显示在图 1中。

图 1
较高频的混叠成份基本上不会引起问题,因为它位于 nyquist 带宽(fs/2)以外。较低频的混叠成份则可能产生问题,因为它可能落在 nyquist 带宽之内,破坏所需要的信号。鉴于采样系统的混叠现象,nyquist 准则要求采样率 fs 》 fa,以避免混叠成份覆盖到第一 nyquist 区。为防止有害的干扰, 任何落在感兴趣的带宽之外的信号(无论是寄生信号或是随机噪声)都应该在抽样之前进行过滤。这就解释了众多采样系统中,加装抗混叠滤波器的必要性。然而,在下面关于次采样的部分中,会表明存在着一些方法,它们可以在信号处理应用中用到混叠现象的益处。
举例来说:对一个最大频率为 10MHz 信号,为了从采样中不失真地重建模拟信号,nyquist 规定采样频率 ³ 20MSPS (每秒百万次抽样)。
但是,我们很快能看出 nyquist 定理的局限性。Nyquist 假定所需的信息带宽等于 nyquist 带宽或采样频率的一半。在图 1 所示的范例中,如果模拟信号 fa 带宽小于 fs/2,那么有可能用低于 nyquist 率进行采样,仍然能够防止混叠现象的产生,并避免损坏所需的信号。应该观察到,所需最小采样频率实际上是输入信号带宽的一个函数,而不仅取决于最大频率成份。Shannon 定理进一步验证了这一结论。
Shannon 信息定理:
一个带宽为 fb 的模拟信号,采样速率必须为 fs 》 2fb,才能避免信息的损失。信号带宽可以从 DC 到 fb(基带采样),或从 f1 到 f2,其中 fb = f2–f1(欠采样)。因此,Shannon 定理表示:实际所需最小采样频率是信号带宽的函数,而不仅取决于它的最大频率成份。通常来说,采样频率至少必须是信号带宽的两倍,并且被采样的信号不能是 fs/2 的整数倍,以防止混叠成份的相互重叠。注意,fMAX(模拟信号的最大频率成份)对于信号带宽 B 的大比例最小采样频率接近 2B。
在许多应用中,这大大地减少了对 ADC 的要求。对一个具有150MHz最大信号频率,但只有10MHz 带宽的信号进行采样,可能只需要一个约 22MSPS 的ADC,而不是 nyquist 规定的 》 300MSPS 的 ADC。
例如,考虑一个带宽为 10MHz、位于 160 –170MHz 频谱范围内的信号。假定按照 Shannon 定理要 30MSPS 的采样率。由于采样过程会产生附带的采样频率,它们是 30MHz 的整数倍,也就是 60MHz(2fs)、90MHz (3fs)。 180MHz 等。介于 160MHz 和 170MHz 之间的所需信号,在这些采样频率的每个谐波(fs、2fs、3fs等)附近都产生混叠。注意:任何一个混叠成份都是原始信号的一个准确表述。30MSPS 采样使得 160–170MHz 的信号被 折返到 0 -10MHz 的第一 nyquist 区。
从本例中还可注意到:可能存在于 ADC 输出 FFT 中的最高频率成份小于或等于采样频率的一半。或者说,由于谐波折返或欠采样,每一个位于 nyquist 带宽之外的 ADC 输入频率成份总被折返到第一 nyquist 区。这可由下列等式表示。而次采样在实用电子系统有许多用途。最常见的欠采样应用是在数字接收器中。首先让我们更详细地解释次抽样的过程。
次抽样或折返的过程可以看作是 ADC 输入信号与采样频率和其谐波的混合。这意味着,许多频率可以混合为 DC,而不再能确认它们的原始频率。举一个 66MSPS 采样频率的例子,则所有输入信号(66–6、66+6、126、136MHz 等等)频率混合为 6MHz,见图 2。每个采样映象折返到 《 FS/2。请注意,图 2 虚线处将发生相位翻转,但这些成份可在软件中去除。如果必须在 ADC 输出处确定原始的输入频率,则无法使用次采样。因为这违反了 nyquist 准则。如果在 ADC 输出处无需确定载波频率,次采样仍然证明有效。这适用于许多通信系统,如手机基站接收器,因为接收器只需恢复载波上的信息,而不是载波本身。我们以一个常见的数字接收器系统为例。

图 2:
射频数字接收器
以使用一个射频载波频率 900MHz(欧洲)和 1800MHz(美国)的 GSM/EDGE 基站为例。一个移动基站接收电路类似图 3 所示。高频射频载波信号首先在混频器和本振级下变频为一个范围 150-190MHz 的中频,供模拟-数字的转换使用。前述 Shannon 定理显示,所必需的采样频率是信号带宽的函数,在 GSM/EDGE 系统中带宽为 200kHz。GSM 系统的动态范围规格需要最小 10 位精度的 ADC,虽然实际都使用 12 位精度。市面上有大量的高速 ADC 可供选择,数字接收器的系统设计师选择器件时必须考虑系统动态范围要求以及器件的成本。由于这些原因,对于 GSM 接收器应用,50-70MSPS 采样率的 ADC 是最常见的选择。虽然在 66MSPS 时 150 –190 兆赫信号为欠采样(使用美国国家半导体的 ADC12DL066, 双 12 位 66MSPS ADC),对于需要的 200kHz 信息带宽,并没有违反 Nyquist 准则。这种选择为 200kHz 的带宽信息信号提供了足够大的空间,同时提供了超过 20dB 的处理增益(下文解释)。请注意,由于种种原因,继续增加采样频率来不断提高处理增益的方法是不切实际的。市面上有更高采样率的 12 位 ADC,譬如 12 位 80MSPS 的 ADC(美国国家半导体 ADC12L080),以及一些 》100MSPS 的 12 位专用 ADC,但低于 100MSPS 和高于 100MSPS 采样率 ADC 之间的成本差别相当大。

图 3: Edge 中常用的接收器
处理增益
ADC 噪声特性通常由热噪声所限制,当选定 ADC 时,其噪声带宽通常被定义作 nyquist 带宽。在 FS = 66MSPS 时,总噪声底限的测量表示为相对于某一输入信号频率处一个 33MHz 带宽内全量程(dBFS)的 dB 值。对于 ADC12L066,150MHz 输入信号频率时的总噪声底限是 –62dBFS。但是对 ADC输出进行过滤后,会产生一个更窄的带宽,例如美国国家半导体的数字式下变频器 CLC5903。滤波过程提供的噪声处理增益是带宽减少量的函数。200kHz 的信道滤波器可获得如下的处理增益:
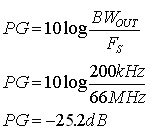
上式假设 ADC 输出的滤波器去除了混叠映象和 Fs 附近的噪声。
这样,200kHz 带宽内的 ADC 输出噪声变成:
62dBFS + (-25.2dB ) = -87.2dBFS。

图 4
表1 重点列出美国国家半导体的几个最新高速 ADC,它们都适用于欠采样应用。对于这些应用,最重要的参数是模拟输入信号带宽、信噪比(SNR),以及有效位数(ENOB)。

总结
当为某个应用选择正确采样率的 ADC 时,不光要知道最高模拟转换频率这一个参数。Shannon 定理显示,信号带宽同等重要。我们发现,高于 Shannon 速率的采样还有其它的好处,如处理增益可以极大地改善动态范围。系统设计师掌握了这一知识,就能在通用且价格合理的标准 ADC 中,正确地选择 ADC 采样频率和精度。

 举报
举报




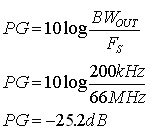



 举报
举报

