正交频分复用(OFDM)是一种多载波调制方式,其基本思想是把高速率的信源信息流通过串并变换后,变换成N路低速率的并行数据流,然后将这N路数据流分别调制到N个相互正交的子载波上并行传输的技术。由于OFDM具有抗多径衰落和频率选择性衰落的能力,同时又能提高系统的频谱利用率等,因此OFDM系统特别适用于多径无线信道环境下高速率数据的传输。但是与单载波系统相比,OFDM系统对同步的要求更加严格,对同步误差更为敏感,如果同步不准确,会直接影响到子载波间的正交性,造成子载波间干扰(ICI)和符号间干扰 (ISI),严重影响OFDM系统的性能。OFDM的同步算法一直是学者们研究的热点,本文通过对经典的Schmidl&Cox时频联合同步算法进行研究,提出了一种改进算法,即基于单训练符号的OFDM联合同步算法。通过软件仿真,得出新的联合同步算法具有更好的同步精度的结论。
1 Schmidl&Cox时频联合同步算法
Schmidl及Cox提出了一种基于训练符号的时频联合同步算法,在这种同步算法中,训练序列选取两个OFDM符号,第一个符号用于符号定时同步以及小数倍频偏的估计;第二个符号用于整数倍频偏的估计。图1显示的是 Schmidl&Cox算法的训练序列结构示意图。
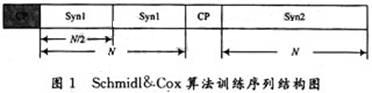
图1中,训练序列第一个符号在时域中由前后相同的两部分组成,第二个训练符号偶数倍子载波上面调制的数据与第一个符号的相应位置的数据具有一种差分关系,整数倍频偏的估计正是利用这种关系来完成的。
由于训练序列中第一个符号的前半部分和后半部分完全相同,所以载波频率偏差对信号造成的影响只是相位偏转。如果前半部分的数据取共轭后,与后半部分的数据对应(间隔T/2)相乘,信道的影响就可以消除了,只会存在φ=πT△f的相位差。在训练符号的起始部分,每一对对应的数据相乘,都会近似存在这个相位,所以求和后这种相位差会累积起来,达到较大的幅度。
Schmidl&Cox算法使用的定时函数可以表示为:
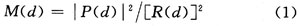
由于M(d)的输出中存在一个“平台”区域,而且这个区域并不精确,因此定时函数的相关峰分布在某个区域范围内。图2给出了高斯信道下M(d)的输出波形。其中,SNR=15 dB,信息数据为4个OFDM符号,每个OFDM符号长度为1 024,循环前缀长度为128,训练序列插入位置位于信息序列的正中间。可见,训练序列区域M(d)的输出幅度明显高于其他信息数据区域,符号定时的完成正是利用了这一特点。

2 时频联合新算法
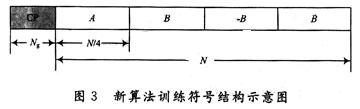
训练符号的结构直接关系到算法的性能,在Schmidl&Cox算法训练序列结构的基础上对其进行一定修改,新的训练符号结构如图3所示。图4显示了这种改造的具体过程。
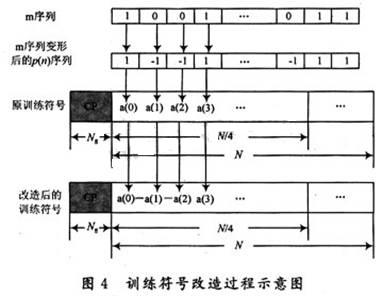
在时域内,训练符号由等长的四部分组成,其中,A本身内部具有重复结构,A与B具有对称共轭关系,数据A的获得,通过将调制后的N/4长度序列进行IFFT的方法实现,这N/4长度序列在偶数子载波位置上发送PN序列,在奇数子载波的位置上发送零,经过IFFT后可以实现数据A本身的重复结构,后将A取对称、共轭后,得到B,再将B取相反数,得到-B。
为了获得更优的符号定时性能,提出的算法思路首先就是避免采用呈现“平台”现象的定时函数,而希望构造的定时函数能在正确的同步位置处形成单一、尖锐的相关峰,更适合采用峰值检测方法来实现符号定时同步。新算法将训练符号进行了改造,具体操作如下:在训练符号第一部分的数据A的前面乘上一个等长的m序列p(n),故第一部分的数据变为p(n)A,训练符号其余三部分的得到方法与上面相同。
因为m序列具有良好的自相关特性,所以p(n)采用映射m序列的方法得到。取长度为N/4的m序列,形式为“0”,“1”序列,映射方法为将序列中的“0”置换为“-1”,变换之后的新序列即为p(n)。需要说明一下,p(n)的引入及构造p(n)时,对m序列所作变形的意义在于在训练符号中随机引入“-1”,“1”,在不对小数倍频偏估计造成影响的基础上,利用其良好的自相关特性,可以进一步优化符号定时同步性能。
根据改造后训练符号的特点,新算法提出的定时函数为:
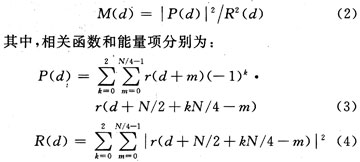
式中:d表示时间序号,每次沿着时间轴移动一个样值,搜索使M(d)达到最大值的时间序号,即为训练符号的起始时刻。符号定时的完成就是通过检验M(d)的最大值来确定的。可以看出,新算法中定时函数的表达式与Schmidl&Cox 算法相同,发生变化的是相关函数表达式P(d)的形式,根据训练序列的特殊结构,相关函数定义为三对数据段运算的总和,又由于训练序列中第三部分数据是第一部分数据对称共轭后的相反数,所以P(d)表达式中又引入了因子(-1)k。
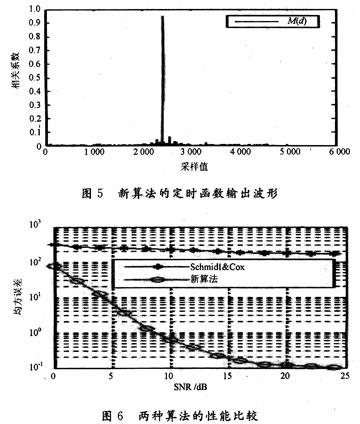
与图2相比,图5所示的新算法的符号定时函数输出波形呈现出类似冲激的峰值,有效地克服了Schmidl&Cox时频联合同步算法中符号定时函数输出波形的顶端平台和波峰两侧数值下降缓慢所带的误差,有利于符号定时同步的精确完成。图6是应用上述两种同步算法对OFDM系统进行仿真时得到的信噪比一均方误差图。
3 结语
从图6中结果可以看出,新算法的符号定时同步性能比 Schmidl&Cox时频联合同步算法的性能有较大幅度提升,而且新算法是在一个训练符号的基础上就达到了与Schmidl&Cox时频联合同步算法相当的频偏估计性能,所用同步开销小,有利于进一步提高OFDM系统的频带利用率。
正交频分复用(OFDM)是一种多载波调制方式,其基本思想是把高速率的信源信息流通过串并变换后,变换成N路低速率的并行数据流,然后将这N路数据流分别调制到N个相互正交的子载波上并行传输的技术。由于OFDM具有抗多径衰落和频率选择性衰落的能力,同时又能提高系统的频谱利用率等,因此OFDM系统特别适用于多径无线信道环境下高速率数据的传输。但是与单载波系统相比,OFDM系统对同步的要求更加严格,对同步误差更为敏感,如果同步不准确,会直接影响到子载波间的正交性,造成子载波间干扰(ICI)和符号间干扰 (ISI),严重影响OFDM系统的性能。OFDM的同步算法一直是学者们研究的热点,本文通过对经典的Schmidl&Cox时频联合同步算法进行研究,提出了一种改进算法,即基于单训练符号的OFDM联合同步算法。通过软件仿真,得出新的联合同步算法具有更好的同步精度的结论。
1 Schmidl&Cox时频联合同步算法
Schmidl及Cox提出了一种基于训练符号的时频联合同步算法,在这种同步算法中,训练序列选取两个OFDM符号,第一个符号用于符号定时同步以及小数倍频偏的估计;第二个符号用于整数倍频偏的估计。图1显示的是 Schmidl&Cox算法的训练序列结构示意图。

图1中,训练序列第一个符号在时域中由前后相同的两部分组成,第二个训练符号偶数倍子载波上面调制的数据与第一个符号的相应位置的数据具有一种差分关系,整数倍频偏的估计正是利用这种关系来完成的。
由于训练序列中第一个符号的前半部分和后半部分完全相同,所以载波频率偏差对信号造成的影响只是相位偏转。如果前半部分的数据取共轭后,与后半部分的数据对应(间隔T/2)相乘,信道的影响就可以消除了,只会存在φ=πT△f的相位差。在训练符号的起始部分,每一对对应的数据相乘,都会近似存在这个相位,所以求和后这种相位差会累积起来,达到较大的幅度。
Schmidl&Cox算法使用的定时函数可以表示为:
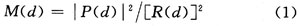
由于M(d)的输出中存在一个“平台”区域,而且这个区域并不精确,因此定时函数的相关峰分布在某个区域范围内。图2给出了高斯信道下M(d)的输出波形。其中,SNR=15 dB,信息数据为4个OFDM符号,每个OFDM符号长度为1 024,循环前缀长度为128,训练序列插入位置位于信息序列的正中间。可见,训练序列区域M(d)的输出幅度明显高于其他信息数据区域,符号定时的完成正是利用了这一特点。

2 时频联合新算法

训练符号的结构直接关系到算法的性能,在Schmidl&Cox算法训练序列结构的基础上对其进行一定修改,新的训练符号结构如图3所示。图4显示了这种改造的具体过程。

在时域内,训练符号由等长的四部分组成,其中,A本身内部具有重复结构,A与B具有对称共轭关系,数据A的获得,通过将调制后的N/4长度序列进行IFFT的方法实现,这N/4长度序列在偶数子载波位置上发送PN序列,在奇数子载波的位置上发送零,经过IFFT后可以实现数据A本身的重复结构,后将A取对称、共轭后,得到B,再将B取相反数,得到-B。
为了获得更优的符号定时性能,提出的算法思路首先就是避免采用呈现“平台”现象的定时函数,而希望构造的定时函数能在正确的同步位置处形成单一、尖锐的相关峰,更适合采用峰值检测方法来实现符号定时同步。新算法将训练符号进行了改造,具体操作如下:在训练符号第一部分的数据A的前面乘上一个等长的m序列p(n),故第一部分的数据变为p(n)A,训练符号其余三部分的得到方法与上面相同。
因为m序列具有良好的自相关特性,所以p(n)采用映射m序列的方法得到。取长度为N/4的m序列,形式为“0”,“1”序列,映射方法为将序列中的“0”置换为“-1”,变换之后的新序列即为p(n)。需要说明一下,p(n)的引入及构造p(n)时,对m序列所作变形的意义在于在训练符号中随机引入“-1”,“1”,在不对小数倍频偏估计造成影响的基础上,利用其良好的自相关特性,可以进一步优化符号定时同步性能。
根据改造后训练符号的特点,新算法提出的定时函数为:
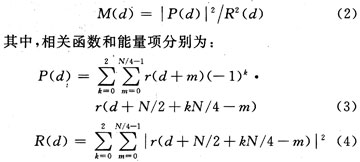
式中:d表示时间序号,每次沿着时间轴移动一个样值,搜索使M(d)达到最大值的时间序号,即为训练符号的起始时刻。符号定时的完成就是通过检验M(d)的最大值来确定的。可以看出,新算法中定时函数的表达式与Schmidl&Cox 算法相同,发生变化的是相关函数表达式P(d)的形式,根据训练序列的特殊结构,相关函数定义为三对数据段运算的总和,又由于训练序列中第三部分数据是第一部分数据对称共轭后的相反数,所以P(d)表达式中又引入了因子(-1)k。
与图2相比,图5所示的新算法的符号定时函数输出波形呈现出类似冲激的峰值,有效地克服了Schmidl&Cox时频联合同步算法中符号定时函数输出波形的顶端平台和波峰两侧数值下降缓慢所带的误差,有利于符号定时同步的精确完成。图6是应用上述两种同步算法对OFDM系统进行仿真时得到的信噪比一均方误差图。

3 结语
从图6中结果可以看出,新算法的符号定时同步性能比 Schmidl&Cox时频联合同步算法的性能有较大幅度提升,而且新算法是在一个训练符号的基础上就达到了与Schmidl&Cox时频联合同步算法相当的频偏估计性能,所用同步开销小,有利于进一步提高OFDM系统的频带利用率。

 举报
举报





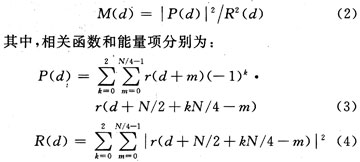


 举报
举报

