在需要硬件实现对数运算的场合,其精度和速度是必须考虑的问题。目前硬件实现对数变换的方法主要有查表法、泰勒公式展开法和线性近似法。查表法所需要的存储单元随着精度的增加或输入值范围的增大而成指数增加;泰勒公式展开法需要乘法器,面积大不易实现;线性近似法的精度有限,且需要误差校正电路,实现较难。
本文利用CORDIC算法在FPGA上实现了高速自然对数变换器。CORDIC算法即坐标旋转数字计算方法最初由J.D.Volder于1959年提出,其基本思想是用一系列与运算基数相关的角度的不断偏摆从而逼近所需旋转的角度。1971年J.S.Walter提出统一的CORDIC算法,把圆周旋转、直线旋转和双曲旋转统一到同一个CORDIC迭代方程里,为同一硬件实现多功能运算提供了前提。由于它将许多复杂的算术运算化成简单的加法和移位操作,在不影响运算速度和精度的情况下,极大的降低了硬件设计的复杂性,节约了硬件资源。利用CORDIC算法可以直接实现乘法、除法、正余弦函数,反正切函数、双曲函数等,对输入进行适当的初始化可以实现正切、双曲正切、对数和指数等函数。
在数字信号处理领域用的较多的是DSP和FPGA。DSP的优势源于多数信号处理算法的乘-累加运算(MAC)都是非常密集的。FPGA通过多极流水线架构也能够用来实现MAC单元,并且FPGA技术可以通过一个芯片上的多级MAC单元来提供更多的带宽,速度可以比数字信号处理芯片快,并且功耗较低。CORDIC算法完全由移位和加法操作完成,因此利用FPGA可以实现更高的运算速度。本文采用流水线结构在FPGA上实现基于CORDIC的对数变换,可以达到80MHz的处理速度。
CORDIC算法实现自然对数运算
CORDIC算法最初是用于计算三角函数的,后来由于其算法的简单、硬件易于实现等多种优势,而被广泛的用于多种初等函数的运算中(包括三角函数、乘除法运算、指数运算、对数运算等)。本文主要利用CORDIC算法的双曲旋转法实现自然对数运算。
在双曲坐标系下,CORDIC算法的迭代方程为:
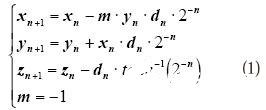
由于

,所以迭代序列必须从n=1开始,为保证迭代序列收敛,因此迭代序列n的取值从第4项开始每隔3n+1项必须重复一次,即n=1,2,3,4,4,5,…,40,40,…。
在向量模式下,

经n次迭代后的输出方程为:

因为

所以令x=t+1,y=t-1
则

所以对于t,如果我们要求lnt,只要做如下初始化:
X=t+1,y=t-1,z=0
则输出z=0.5ln(t),只需要在CORDIC之后做一次左移即可。
如(2)式所示,为保证迭代序列的收敛,|tanh-1(y0/x0)|≤1.1182,因此|y/x|max≈0.8069,n→∞,反双曲正切的定义域为(-1,1),可见函数的输入范围受到了限制。解决的方法是增加n为负数的迭代,改进的算法公式为:
当n≤0时
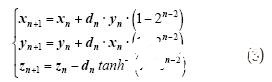
当n》0时

收敛的范围变成
|tanh-1(y/x)|≤θmax
其中

当M=5时,θmax=12.4264,函数tanh-1的范围是[-12.4264,12.4264]。也就是说此时y/x可以接近于[-1,1],几乎覆盖tanh-1的整个定义域。因此硬件实现过程中可以从-5开始迭代。
对数运算的FPGA实现
实现方法
·预处理单元
欲利用CORDIC方法求自然对数,必须对输入进行初始化,经迭代运算后才能得到对数运算值。该对数变换器的输入为16位数,在预处理单元中将输入分别加减一,并将位宽扩大为40位,最高位作为符号位覆值给第一次迭代的x0和y0,如图1所示,图中s代表符号位。扩大位宽可以提高输出精度。

图1初始迭代值x0,y0
·CORDIC单元
CORDIC单元是实现对数变换器的核心。本文利用流水线结构实现CORDIC算法,其结构如图2所示。在设计中,采用由28级CORDIC运算单元组成的流水线结构,为扩大输入范围,从n=-5开始迭代,移位序列为[7,6,5,4,3,2,1,2…28]。前6级根据(3)式进行迭代,后22级根据(4)式进行迭代。经过28级流水线运算后,y变为0,z左移一位就是要求的对数值。每一级电路结构主要包括2个移位寄存器和3个加减法器,这些移位寄存器各自有不同的固定的移位次数,加减法选择由该级中y的最高位(符号位)决定。θn为第n次迭代的旋转角度,并作为常数直接连到了累加器上,不需要存储空间和读取时间。

图2CORDIC流水线结构
·后处理单元
由CORDIC得到的z=1/2ln(t),因此将结果左移一位,并截取高16位作为最终的输出。其中最高位为符号位,最大输入值65535的对数值为11.0903,对应的输出为7FFF,其余输出均除以对应的值即得到相应的对数值。
实验结果
在QuartusII5.1软件环境下使用VerilogHDL语言完成了上述各算法,并在cyclone系列芯片EP1C6Q240C8上实现。图3为对数运算时序仿真图。表1为对数运算结果与理论值的比较。

图3对数运算时序仿真图
由表1可看出,该对数运算器的输出误差为10-4数量级。由于采用流水线结构,能够在执行进程的同时输入数据,从而极大的提高了程序的运行效率。该设计需要30个时钟周期获取第一个计算结果,而只需要一个时钟周期来获取随后的计算结果。利用QuartusⅡ5.1软件进行时序分析,该运算器的最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。
表1对数运算结果与理论值的比较

结语
利用对数变换可以将乘除法变换为加减法实现,有利于乘除法在硬件中的实现。由于CORDIC算法完全由移位和相加运算完成,降低了复杂性,易于硬件的实现。利用CORDIC算法在FPGA上设计了一种自然对数变换器。实现过程中采用流水线结构,提高了系统的运行效率。实验结果表明该对数运算器的输出误差为10-4数量级,最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。
在需要硬件实现对数运算的场合,其精度和速度是必须考虑的问题。目前硬件实现对数变换的方法主要有查表法、泰勒公式展开法和线性近似法。查表法所需要的存储单元随着精度的增加或输入值范围的增大而成指数增加;泰勒公式展开法需要乘法器,面积大不易实现;线性近似法的精度有限,且需要误差校正电路,实现较难。
本文利用CORDIC算法在FPGA上实现了高速自然对数变换器。CORDIC算法即坐标旋转数字计算方法最初由J.D.Volder于1959年提出,其基本思想是用一系列与运算基数相关的角度的不断偏摆从而逼近所需旋转的角度。1971年J.S.Walter提出统一的CORDIC算法,把圆周旋转、直线旋转和双曲旋转统一到同一个CORDIC迭代方程里,为同一硬件实现多功能运算提供了前提。由于它将许多复杂的算术运算化成简单的加法和移位操作,在不影响运算速度和精度的情况下,极大的降低了硬件设计的复杂性,节约了硬件资源。利用CORDIC算法可以直接实现乘法、除法、正余弦函数,反正切函数、双曲函数等,对输入进行适当的初始化可以实现正切、双曲正切、对数和指数等函数。
在数字信号处理领域用的较多的是DSP和FPGA。DSP的优势源于多数信号处理算法的乘-累加运算(MAC)都是非常密集的。FPGA通过多极流水线架构也能够用来实现MAC单元,并且FPGA技术可以通过一个芯片上的多级MAC单元来提供更多的带宽,速度可以比数字信号处理芯片快,并且功耗较低。CORDIC算法完全由移位和加法操作完成,因此利用FPGA可以实现更高的运算速度。本文采用流水线结构在FPGA上实现基于CORDIC的对数变换,可以达到80MHz的处理速度。
CORDIC算法实现自然对数运算
CORDIC算法最初是用于计算三角函数的,后来由于其算法的简单、硬件易于实现等多种优势,而被广泛的用于多种初等函数的运算中(包括三角函数、乘除法运算、指数运算、对数运算等)。本文主要利用CORDIC算法的双曲旋转法实现自然对数运算。
在双曲坐标系下,CORDIC算法的迭代方程为:
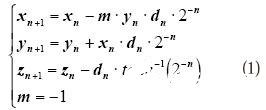
由于

,所以迭代序列必须从n=1开始,为保证迭代序列收敛,因此迭代序列n的取值从第4项开始每隔3n+1项必须重复一次,即n=1,2,3,4,4,5,…,40,40,…。
在向量模式下,

经n次迭代后的输出方程为:

因为

所以令x=t+1,y=t-1
则

所以对于t,如果我们要求lnt,只要做如下初始化:
X=t+1,y=t-1,z=0
则输出z=0.5ln(t),只需要在CORDIC之后做一次左移即可。
如(2)式所示,为保证迭代序列的收敛,|tanh-1(y0/x0)|≤1.1182,因此|y/x|max≈0.8069,n→∞,反双曲正切的定义域为(-1,1),可见函数的输入范围受到了限制。解决的方法是增加n为负数的迭代,改进的算法公式为:
当n≤0时
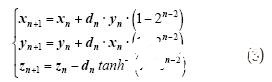
当n》0时

收敛的范围变成
|tanh-1(y/x)|≤θmax
其中

当M=5时,θmax=12.4264,函数tanh-1的范围是[-12.4264,12.4264]。也就是说此时y/x可以接近于[-1,1],几乎覆盖tanh-1的整个定义域。因此硬件实现过程中可以从-5开始迭代。
对数运算的FPGA实现
实现方法
·预处理单元
欲利用CORDIC方法求自然对数,必须对输入进行初始化,经迭代运算后才能得到对数运算值。该对数变换器的输入为16位数,在预处理单元中将输入分别加减一,并将位宽扩大为40位,最高位作为符号位覆值给第一次迭代的x0和y0,如图1所示,图中s代表符号位。扩大位宽可以提高输出精度。

图1初始迭代值x0,y0
·CORDIC单元
CORDIC单元是实现对数变换器的核心。本文利用流水线结构实现CORDIC算法,其结构如图2所示。在设计中,采用由28级CORDIC运算单元组成的流水线结构,为扩大输入范围,从n=-5开始迭代,移位序列为[7,6,5,4,3,2,1,2…28]。前6级根据(3)式进行迭代,后22级根据(4)式进行迭代。经过28级流水线运算后,y变为0,z左移一位就是要求的对数值。每一级电路结构主要包括2个移位寄存器和3个加减法器,这些移位寄存器各自有不同的固定的移位次数,加减法选择由该级中y的最高位(符号位)决定。θn为第n次迭代的旋转角度,并作为常数直接连到了累加器上,不需要存储空间和读取时间。

图2CORDIC流水线结构
·后处理单元
由CORDIC得到的z=1/2ln(t),因此将结果左移一位,并截取高16位作为最终的输出。其中最高位为符号位,最大输入值65535的对数值为11.0903,对应的输出为7FFF,其余输出均除以对应的值即得到相应的对数值。
实验结果
在QuartusII5.1软件环境下使用VerilogHDL语言完成了上述各算法,并在cyclone系列芯片EP1C6Q240C8上实现。图3为对数运算时序仿真图。表1为对数运算结果与理论值的比较。

图3对数运算时序仿真图
由表1可看出,该对数运算器的输出误差为10-4数量级。由于采用流水线结构,能够在执行进程的同时输入数据,从而极大的提高了程序的运行效率。该设计需要30个时钟周期获取第一个计算结果,而只需要一个时钟周期来获取随后的计算结果。利用QuartusⅡ5.1软件进行时序分析,该运算器的最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。
表1对数运算结果与理论值的比较

结语
利用对数变换可以将乘除法变换为加减法实现,有利于乘除法在硬件中的实现。由于CORDIC算法完全由移位和相加运算完成,降低了复杂性,易于硬件的实现。利用CORDIC算法在FPGA上设计了一种自然对数变换器。实现过程中采用流水线结构,提高了系统的运行效率。实验结果表明该对数运算器的输出误差为10-4数量级,最高频率可达到80MHz。该运算器适用于高速大数据量的数据处理。

 举报
举报





 举报
举报

