除法器是电子技术领域的基础模块,在电子电路设计中得到广泛应用。目前,实现除法器的方法有硬件实现和软件实现两种方法。硬件实现的方法主要是以硬件的消耗为代价,从而有实现速度快的特点。用硬件的方法来实现除法器的研究很多,如利用微处理器实现快速乘除法运算,FPGA实现二进制除法运算,模拟除法器等;而通过软件实现的除法器算法,可以大大提高器件的工作频率和设计的灵活性,可以从总体上提高设计性能,而设计高效实用的算法是除法器的关键,故除法器的算法研究成为现今热点。
目前,软件方面主要是通过减法算法来实现除法运算,把被除数作为被减数,除数作为减数,作减法,直到被减数小于减数为止,记录能够相减的次数即得到商的整数部分。将所得的余数乘以10作为被减数,除数作为减数,作减法,差重新置入被减数,反复相减,直到被减数小于减数为止,记录能够相减的次数即得到商的十分位数值。依此继续下去,可得到商的百分位数值,千分位数值,……,要精确到哪一位,就依次做到哪一位。此方法的缺点是速度慢,而且最后一位的精度不高,为了克服以上的缺点,这里设计一种算法在软件上改进了除法器运算的准确性和处理速度。
1 设计方法
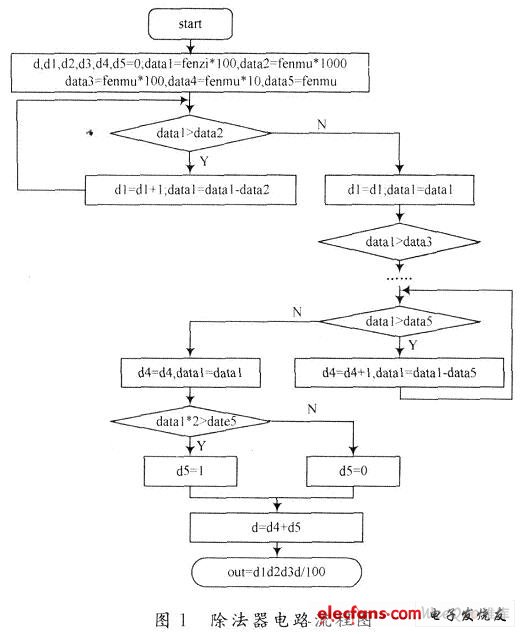
对于任意给定的两个整数fenzi和fenmu,设fenzi为被除数,fenmu为除数。为了得到两个数相除的十进制结果,本设计主要通过下面的算法来实现,假如要保留小数点后面的n位有效数字,首先把fenzi乘以10的n次方,赋值给寄存器变量dataO;接着把fenmu分别乘以10的(n+m),(n+m一1),(n+m一2),…,1,O次方分别赋值给(n+m+1)个不同的变量data(n+m+1),data(n+m),…,datal,其中m是fenzi和fenmu的位数之差(当fenzi的位数多于fenmu时,m为正,否则为负);先求出商的最高位的值,如果dataO大于data(n+m+1),则计数器自动加1,再把dataO和data(n+m+1)的差值赋给data0,再相减直到data0的值小于data(n+m+1),此时计数器的计数值就是最高位的值;依此用同样的方法继续下去,就可得到各个位上的值。对最后一位进行四舍五入处理,当相减后的dataO
2 仿真结果及分析
对上述的流程图用Verilog描述语言编程,在Ca—dence的NC—Verilog仿真器下仿真,设输入的Ienzi和fenmu的值分别为128和11,仿真波形如图2所示。

从图2的波形可以看出,输出结果为1 164,除法运算要精确到百分位,所以往左移动2位,其最终的值为11.64,而实际的值为11.636 36……,经过四舍五入得到的结果完成正确。从仿真时间来看,对于相同的数值输入,本设计只用了12个脉冲,而普通除法器至少需要20个脉冲(128/11=11余7,70/11=*,40/11=3余7,1l+6+3=20),相比之下本设计的除法算法有很大的优势。
然而对于两个位数相差很大的数相除,则本设计的速度优势更加的明显,本设计每一位的运行时间都不会超过9个时钟脉冲,因此进行,z位计算的总脉冲也不会超过9n个,而传统的除法运算需要多个时钟脉冲,一般会是本设计时钟脉冲的数倍。该算法同样适合小数的运算,只要把小数化成整数,再做同样的处理,就可以得到精确的结果。
3 结 语
通过对除法器算法的改进,用四舍五入的方法对数据进行处理,使得到的结果准确性有了进一步的提高;运用移位、循环减法,实现数据的高速运算,并能任意设定计算的精度。运用此方法在软件方面设计除法器对速度和准确性的提高有积极意义。
除法器是电子技术领域的基础模块,在电子电路设计中得到广泛应用。目前,实现除法器的方法有硬件实现和软件实现两种方法。硬件实现的方法主要是以硬件的消耗为代价,从而有实现速度快的特点。用硬件的方法来实现除法器的研究很多,如利用微处理器实现快速乘除法运算,FPGA实现二进制除法运算,模拟除法器等;而通过软件实现的除法器算法,可以大大提高器件的工作频率和设计的灵活性,可以从总体上提高设计性能,而设计高效实用的算法是除法器的关键,故除法器的算法研究成为现今热点。
目前,软件方面主要是通过减法算法来实现除法运算,把被除数作为被减数,除数作为减数,作减法,直到被减数小于减数为止,记录能够相减的次数即得到商的整数部分。将所得的余数乘以10作为被减数,除数作为减数,作减法,差重新置入被减数,反复相减,直到被减数小于减数为止,记录能够相减的次数即得到商的十分位数值。依此继续下去,可得到商的百分位数值,千分位数值,……,要精确到哪一位,就依次做到哪一位。此方法的缺点是速度慢,而且最后一位的精度不高,为了克服以上的缺点,这里设计一种算法在软件上改进了除法器运算的准确性和处理速度。
1 设计方法
对于任意给定的两个整数fenzi和fenmu,设fenzi为被除数,fenmu为除数。为了得到两个数相除的十进制结果,本设计主要通过下面的算法来实现,假如要保留小数点后面的n位有效数字,首先把fenzi乘以10的n次方,赋值给寄存器变量dataO;接着把fenmu分别乘以10的(n+m),(n+m一1),(n+m一2),…,1,O次方分别赋值给(n+m+1)个不同的变量data(n+m+1),data(n+m),…,datal,其中m是fenzi和fenmu的位数之差(当fenzi的位数多于fenmu时,m为正,否则为负);先求出商的最高位的值,如果dataO大于data(n+m+1),则计数器自动加1,再把dataO和data(n+m+1)的差值赋给data0,再相减直到data0的值小于data(n+m+1),此时计数器的计数值就是最高位的值;依此用同样的方法继续下去,就可得到各个位上的值。对最后一位进行四舍五入处理,当相减后的dataO

2 仿真结果及分析
对上述的流程图用Verilog描述语言编程,在Ca—dence的NC—Verilog仿真器下仿真,设输入的Ienzi和fenmu的值分别为128和11,仿真波形如图2所示。

从图2的波形可以看出,输出结果为1 164,除法运算要精确到百分位,所以往左移动2位,其最终的值为11.64,而实际的值为11.636 36……,经过四舍五入得到的结果完成正确。从仿真时间来看,对于相同的数值输入,本设计只用了12个脉冲,而普通除法器至少需要20个脉冲(128/11=11余7,70/11=*,40/11=3余7,1l+6+3=20),相比之下本设计的除法算法有很大的优势。
然而对于两个位数相差很大的数相除,则本设计的速度优势更加的明显,本设计每一位的运行时间都不会超过9个时钟脉冲,因此进行,z位计算的总脉冲也不会超过9n个,而传统的除法运算需要多个时钟脉冲,一般会是本设计时钟脉冲的数倍。该算法同样适合小数的运算,只要把小数化成整数,再做同样的处理,就可以得到精确的结果。
3 结 语
通过对除法器算法的改进,用四舍五入的方法对数据进行处理,使得到的结果准确性有了进一步的提高;运用移位、循环减法,实现数据的高速运算,并能任意设定计算的精度。运用此方法在软件方面设计除法器对速度和准确性的提高有积极意义。

 举报
举报




 举报
举报

