在数字信号处理领域,滤波器无疑是个非常重要的环节。而在数字滤波器中,有限脉冲响应(FIR)滤波器因为其线性相位的特点,应用尤为广泛。实际应用中FIR滤波器分为常系数FIR滤波器和变系数FIR滤波器。常系数FIR滤波器的系数固定不变,可根据其特点采用分布式算法进行设计,故实现起来速度快,消耗的资源少。变系数FIR滤波器的系数是不断变化的。当前含有变系数FIR滤波环节的芯片普遍存在速度与处理级数的矛盾,有效解决此问题具有重要的现实意义。
随着片上系统(SOC)时代的到来,可编程逻辑器件不仅为FIR滤波器的设计提供了一条可行而高效的方法,而且更被广泛地使用于数字信号处理的各个领域。采用INMOS公司的IMS A100级联型信号处理器为模板,以FIR滤波器设计为核心,用FPGA技术开发设计级联型信号处理器,能够应用于数字FIR滤波、高速自适应滤波、相关和卷积、离散傅里叶变换、脉冲压缩、线性预测编码语音处理、高速定点矩阵乘法等,有较好的应用前景和发展空间。
1 FIR滤波器结构设计
传统的FIR滤波器横向结构如图1(a)所示,为提高系统处理速度,求和单元∑可采用流水线结构。图中的N阶滤波器从系统开始工作到第一个输出数据有效,需经过N个周期,系统最大速度是由一次乘法和N个乘法结果求和运算消耗的时间决定,因而运算速度很低。采用流水线结构后,运算速度则由一次乘法运算决定,运算速度得到提高。为了系统结构的有效设计,根据FIR滤波器结构的可逆性,可采用图1(b)所示的转置结构。
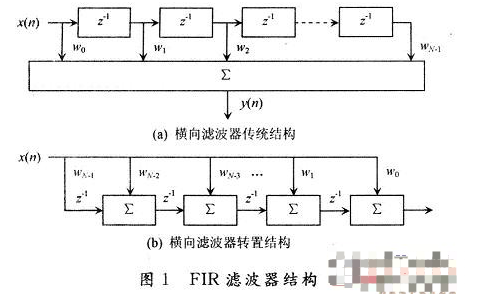
在横向滤波器的转置结构中,N个相同的处理单元级联就组成了滤波器,因此系统能在保证计算结果不溢出的前提下,只改变级联处理单元的数目就能方便地调整滤波器的级数。在t=KT时,滤波器的输出为:
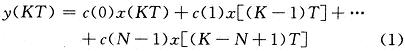
实际应用中常常会用到高阶FIR滤波器,但一块芯片的资源和容量毕竟有限,不能很好地满足设计要求。从图1(b)所示的结构可以看出,多片FIR滤波器可以级联起来,构成高阶FIR滤波器,无需任何附加逻辑,也不会降低运算速度,同时保持运算精度,故对比后优先选择图1(b)的滤波器转置结构。
考虑到FIR滤波器系数的对称性,在横向滤波器的转置结构中再加入一条反向相加、延时支路,把单片FIR滤波器的级数由N扩展到2N,适合于阶数M为N<M≤2N的滤波器使用。系统只需用一个信号便可实现对芯片级联使用或单片使用的控制,具体实现结构如图2所示。
为了让设计的信号处理器能用于自适应信号处理、快速傅里叶变换等领域,还必须使系统能根据用户的要求实时改变当前系数。一般有两种方案可以实现:一是通过一个写入端口直接修改当前系数;二是准备多组备用系数,并可以在与系统工作时钟异步的情况下对这些备用系数进行修改。方案一可以节省一定的系统资源,但对一组当前系数的修改需要较长时间,且此段时间内系统无法正常工作,故实时性较差;方案二虽然消耗了较多的系统资源,但系统能在准备系数(即修改备用系数)时正常工作,修改当前系数只需将当前系数和备用系数交换,交换系数的过程只需一个时钟节拍即可完成。综合考虑各方面因素,方案二具备更好的系统性能,故优先选择方案二。
2 系统设计与FPGA实现
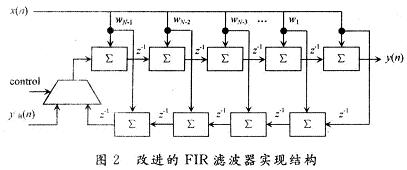
图2的FIR滤波器结构是高速、高精度的数字式横向滤波器结构,在数字信号处理应用中可作为功能块,完成高速离散傅里叶变换、卷积和相关,以及滤波功能。级联型信号处理器的设计正是基于此结构,其FPGA实现的总体结构如图3所示。
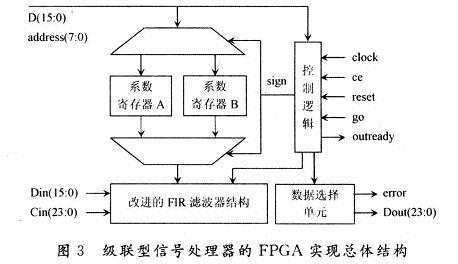
此级联型信号处理器的外部输入数据Din字长16位,系数字长16位,输入数据和系数均采用二进制补码方式。内部有A,B两组系数寄存器,一个存储当前系数,另一个存储修改系数,用户可通过数据线D在与系统时钟异步的情况下对系数进行修改,也可使A,B两组系数在系统工作的过程中相互“交换”。系统具有用户控制切换和系统自动切换两种系数切换方式。为了保持完整的数据精度,对于延时、乘法和相加链的中间结果是以满精度进行运算的,若N=2K,则系统的满精度为31+K位,考虑到单片使用时N级可扩展到2N级,所以应选用的满精度为32+K位,本系统采用32阶滤波器设计,故满精度为37位。在延时、乘法和相加链的输出端,设计一个可编程的桶形移位器(即数据选择单元),它可从四组24位数据字段[7~30],[11~34],[15~38]和[20~43]字段中任选一种,这四组字段从FIR滤波器输出的37位结果[0~36]中得到,所选的24位在输出前需进行舍入或符号扩展,至于如何选择,则根据实际应用而定。另外,本系统还为用户提供了系统复位(reset)、工作许可(go)、状态监测(error,out-ready)等常用握手信号。用户可以读写控制逻辑中的状态控制寄存器来切换当前系数,选择输出字段和设置系统工作模式(单片或级联,当系统课用于级联时,Cin为级联输入),其内部寄存器的详细描述见表1。

用户还可以通过数据线D、地址信号address、读写控制信号W、系统使能信号Ce、片选信号Cs等对系数寄存器A,B以及状态控制寄存器进行读写。
3 FPGA仿真
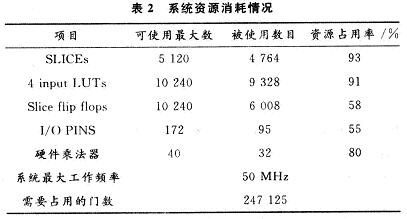
系统利用FPGA实现了一个32阶的级联型信号处理器,选用的FPGA芯片是XILINX公司的集成了18×18位硬件乘法器的VirtexⅡ系列的XC2V1000-5-FG256,其资源消耗情况如表2所示。
为了方便仿真和结果观察,选用固定值输入,图4(a)和图4(b)分别是系统级联型工作模式及系数切换仿真和系统单片工作模式仿真结果。
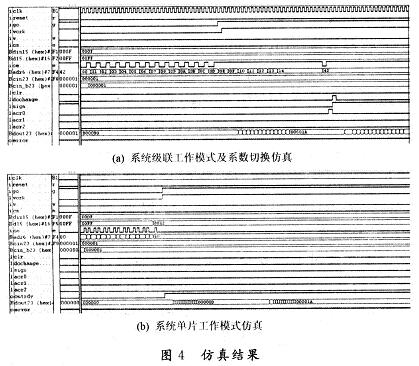
从图4(a)和图4(b)可以看出,系数寄存器和内部控制寄存器可以正确读写,当输入系数切换指令后,系数正常交换,整个系统工作正常。
4 性能分析
系统的输入数据和系数都是16位的二进制补码,所以中间结果的[0~30]字段对应着-1~+1。而系统的中间结果是以满精度运算的,所以系统输出的误差产生于数据选择单元,四组字段会产生不同的误差。
对[7~30]字段,按四舍五入原则产生的最大舍入误差为:

系统的仿真结果和性能分析都表明,系统可正常工作,且最高工作时钟可达到50 MHz。
5 结语
讨论了级联型信号处理器的FPGA高效实现,通过系统论证、仿真和硬件调试证明,设计方法正确有效,系统功能实现正常且稳定,为FIR滤波、快速傅里叶变换、自适应滤波等应用提供了一条可行之路,其性能可以随着可编程逻辑器件的发展而不断提高。
在数字信号处理领域,滤波器无疑是个非常重要的环节。而在数字滤波器中,有限脉冲响应(FIR)滤波器因为其线性相位的特点,应用尤为广泛。实际应用中FIR滤波器分为常系数FIR滤波器和变系数FIR滤波器。常系数FIR滤波器的系数固定不变,可根据其特点采用分布式算法进行设计,故实现起来速度快,消耗的资源少。变系数FIR滤波器的系数是不断变化的。当前含有变系数FIR滤波环节的芯片普遍存在速度与处理级数的矛盾,有效解决此问题具有重要的现实意义。
随着片上系统(SOC)时代的到来,可编程逻辑器件不仅为FIR滤波器的设计提供了一条可行而高效的方法,而且更被广泛地使用于数字信号处理的各个领域。采用INMOS公司的IMS A100级联型信号处理器为模板,以FIR滤波器设计为核心,用FPGA技术开发设计级联型信号处理器,能够应用于数字FIR滤波、高速自适应滤波、相关和卷积、离散傅里叶变换、脉冲压缩、线性预测编码语音处理、高速定点矩阵乘法等,有较好的应用前景和发展空间。
1 FIR滤波器结构设计
传统的FIR滤波器横向结构如图1(a)所示,为提高系统处理速度,求和单元∑可采用流水线结构。图中的N阶滤波器从系统开始工作到第一个输出数据有效,需经过N个周期,系统最大速度是由一次乘法和N个乘法结果求和运算消耗的时间决定,因而运算速度很低。采用流水线结构后,运算速度则由一次乘法运算决定,运算速度得到提高。为了系统结构的有效设计,根据FIR滤波器结构的可逆性,可采用图1(b)所示的转置结构。

在横向滤波器的转置结构中,N个相同的处理单元级联就组成了滤波器,因此系统能在保证计算结果不溢出的前提下,只改变级联处理单元的数目就能方便地调整滤波器的级数。在t=KT时,滤波器的输出为:
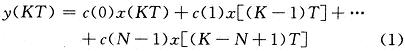
实际应用中常常会用到高阶FIR滤波器,但一块芯片的资源和容量毕竟有限,不能很好地满足设计要求。从图1(b)所示的结构可以看出,多片FIR滤波器可以级联起来,构成高阶FIR滤波器,无需任何附加逻辑,也不会降低运算速度,同时保持运算精度,故对比后优先选择图1(b)的滤波器转置结构。
考虑到FIR滤波器系数的对称性,在横向滤波器的转置结构中再加入一条反向相加、延时支路,把单片FIR滤波器的级数由N扩展到2N,适合于阶数M为N<M≤2N的滤波器使用。系统只需用一个信号便可实现对芯片级联使用或单片使用的控制,具体实现结构如图2所示。

为了让设计的信号处理器能用于自适应信号处理、快速傅里叶变换等领域,还必须使系统能根据用户的要求实时改变当前系数。一般有两种方案可以实现:一是通过一个写入端口直接修改当前系数;二是准备多组备用系数,并可以在与系统工作时钟异步的情况下对这些备用系数进行修改。方案一可以节省一定的系统资源,但对一组当前系数的修改需要较长时间,且此段时间内系统无法正常工作,故实时性较差;方案二虽然消耗了较多的系统资源,但系统能在准备系数(即修改备用系数)时正常工作,修改当前系数只需将当前系数和备用系数交换,交换系数的过程只需一个时钟节拍即可完成。综合考虑各方面因素,方案二具备更好的系统性能,故优先选择方案二。
2 系统设计与FPGA实现
图2的FIR滤波器结构是高速、高精度的数字式横向滤波器结构,在数字信号处理应用中可作为功能块,完成高速离散傅里叶变换、卷积和相关,以及滤波功能。级联型信号处理器的设计正是基于此结构,其FPGA实现的总体结构如图3所示。

此级联型信号处理器的外部输入数据Din字长16位,系数字长16位,输入数据和系数均采用二进制补码方式。内部有A,B两组系数寄存器,一个存储当前系数,另一个存储修改系数,用户可通过数据线D在与系统时钟异步的情况下对系数进行修改,也可使A,B两组系数在系统工作的过程中相互“交换”。系统具有用户控制切换和系统自动切换两种系数切换方式。为了保持完整的数据精度,对于延时、乘法和相加链的中间结果是以满精度进行运算的,若N=2K,则系统的满精度为31+K位,考虑到单片使用时N级可扩展到2N级,所以应选用的满精度为32+K位,本系统采用32阶滤波器设计,故满精度为37位。在延时、乘法和相加链的输出端,设计一个可编程的桶形移位器(即数据选择单元),它可从四组24位数据字段[7~30],[11~34],[15~38]和[20~43]字段中任选一种,这四组字段从FIR滤波器输出的37位结果[0~36]中得到,所选的24位在输出前需进行舍入或符号扩展,至于如何选择,则根据实际应用而定。另外,本系统还为用户提供了系统复位(reset)、工作许可(go)、状态监测(error,out-ready)等常用握手信号。用户可以读写控制逻辑中的状态控制寄存器来切换当前系数,选择输出字段和设置系统工作模式(单片或级联,当系统课用于级联时,Cin为级联输入),其内部寄存器的详细描述见表1。

用户还可以通过数据线D、地址信号address、读写控制信号W、系统使能信号Ce、片选信号Cs等对系数寄存器A,B以及状态控制寄存器进行读写。
3 FPGA仿真
系统利用FPGA实现了一个32阶的级联型信号处理器,选用的FPGA芯片是XILINX公司的集成了18×18位硬件乘法器的VirtexⅡ系列的XC2V1000-5-FG256,其资源消耗情况如表2所示。

为了方便仿真和结果观察,选用固定值输入,图4(a)和图4(b)分别是系统级联型工作模式及系数切换仿真和系统单片工作模式仿真结果。

从图4(a)和图4(b)可以看出,系数寄存器和内部控制寄存器可以正确读写,当输入系数切换指令后,系数正常交换,整个系统工作正常。
4 性能分析
系统的输入数据和系数都是16位的二进制补码,所以中间结果的[0~30]字段对应着-1~+1。而系统的中间结果是以满精度运算的,所以系统输出的误差产生于数据选择单元,四组字段会产生不同的误差。
对[7~30]字段,按四舍五入原则产生的最大舍入误差为:

系统的仿真结果和性能分析都表明,系统可正常工作,且最高工作时钟可达到50 MHz。
5 结语
讨论了级联型信号处理器的FPGA高效实现,通过系统论证、仿真和硬件调试证明,设计方法正确有效,系统功能实现正常且稳定,为FIR滤波、快速傅里叶变换、自适应滤波等应用提供了一条可行之路,其性能可以随着可编程逻辑器件的发展而不断提高。

 举报
举报









 举报
举报

