引言
在变容二极管调频电路中,载频频率的不稳定性主要由温度变化、电源电压变化、负载阻抗变化等因素引起的。可以通过减少外界因素的变化来提高频率稳定度,如采用高稳定度直流稳压电源来减少电源电压的变化,采用金属屏蔽罩减少外界电磁场的变化,或者提高谐振回路的标准性,如采用参数稳定的回路电感器和电容器,采用温度补偿法,改进安装工艺,减弱振荡管与谐振回路的耦合。
在以上这些措施中,温度补偿法得到了广泛的应用。尤其是在军工产品方面,为了满足产品在高、低温环境下的工作性能要求,常常通过温度补偿法来减少温度对产品各项指标的影响。在变容二极管调频电路中,控制变容二极管的反向电压的轻微变动会导致频率偏移,在电路设计中,载频受温度变化的影响,通常规律是温度升高时频率变高,温度降低时载频瞬时起振频率偏低。如何兼顾高低温时的频率偏移,本文提供了一个简单的补偿电路,很好地解决了这个问题。
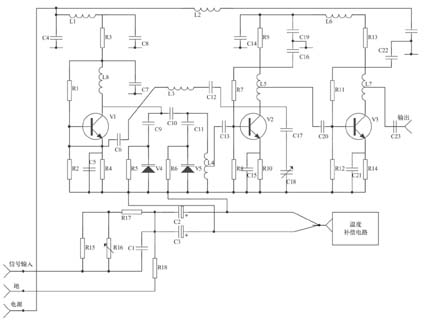
温度补偿的理论分析和模型
● 变容二极管调频电路的分析
变容二极管的调频电路如图1所示,在电路中,载频受温度的影响,通常规律是负的温度系数,即温度升高时频率变低,可以用具有负温度系数的电容来补偿。补偿用电容是C6、C12、C18,所用温度系数组别是C组。C9、C10、C11对失真度有较大的影响,可以选用一定温度系数电容来对失真度进行温度补偿,由于频率高、分散性大,没有较确切的规律可循,一般要靠试验确定,改变范围通常不宜过大,以调高或调低一挡为宜,个别电容可以改变到两挡。电感L2、L3、L4采用在高频陶瓷骨架上烧渗银制成的温度系数小、损耗小、Q值高的电感线圈,其Q值大于200,温度系数可达(1~5)×10-7/℃,防振性能好。另外还加了一个声表面波延迟线以对准频率,有时可能会产生自激,首先要找准自激发生在哪级,然后在该级回路中并以恰当的电阻。采用了以上措施,在常态下,调频电路的载频稳定度小于10-6。
一般情况下电感具有正温度系数,而电容根据不同介电材料,其温度系数可正可负。因此,选择合适的具有不同温度系数的电感和电容,同时接入谐振回路,从而使因温度变化引起的电感和电容值的变化互相抵消,使回路总电抗量变化减小。实际上,由于电感、电容大小随温度变化的非线性和晶体管极间电容和其他分布杂散电容的影响,在高低温时,频率的偏移往往较大。由此,考虑用可控制的电容变化抵消不确定的电感、电容变化。变容二极管上的电压包括直流电压和调制信号电压,通过控制直流电压即可达到目的。
● 温度补偿理论
要提高频率稳定度,回路的标准性越高越好。
设回路的总电感为L,总电容为C,回路的谐振频率为
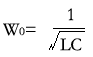
若温度变化引起L和C的微小变化分别为L和C,则W的变化量为
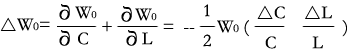
即
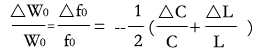
设电容量和电感量的相对变化值用βc和βl表示,则
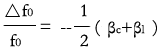
要提高频率稳定度,则必须是(βc+βl )的值越小越好,或者使βc、βl的数值符号相反,相互抵消。
在变容二极管调频电路中,变容二极管上的电压变化直接影响到频率的变化。通过电压控制电容的变化以抵消电感的变化。而变容二极管上的电压在不同温度状态下,差异很大。其电压—温度曲线如图2所示。
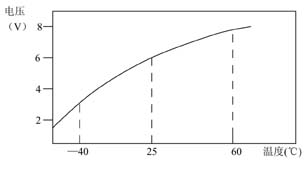
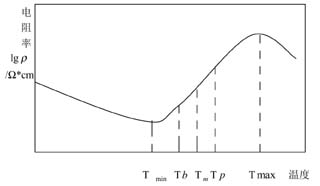
采用一般的电阻串、并联不能达到如此大的电压差异,需引入正温度系数(PTC)的热敏电阻。正温度系数热敏电阻材料主要有BaTiO3系陶瓷。BaTiO3热敏电阻器典型的阻温曲线如图3所示。可以看出,电阻率ρ首先随温度的升高而下降,当温度达到Tmin时,电阻率ρ达到最低值。之后ρ随T的升高而升高。当温度达到Tb以后,ρ随温度急剧升高,这一温度称为开关温度。温度为Tm时,电阻温度系数达到最大值,这时ρ与T几乎成直线关系。达到Tp之后,曲线弯曲,电阻温度系数迅速降低。当温度升高到Tmax之后,ρ重新随温度升高而降低。尤其要注意在居里温度以上,势垒急剧升高,电子跃迁变得困难,阻值剧增几个数量级以上的PTC现象。这时通过热敏电阻分压后到达变容二极管的电压会突然变小,因此设计中要消除或尽量减小PTC现象对电路的不良影响。通过合理的设计,即可使变容二极管上的电压在不同温度状态下都得到满足。
● 温度补偿的电路模型
综上所述,电路模型如图4所示。

在电路中,当温度升高,热敏电阻R7阻值变大。串并联电路(R5+R7)||R6的阻值变大,分压后加在变容二极管上的电压减小,当温度降低,(R5+R7)||R6的阻值变小,分压后加在变容二极管的电压增大。变容二极管上的电压变大变小的范围主要由R5、R6、R7调节,电阻R3、R4、R8、R9进行微调。一般情况下,R5、R6的阻值要小于热敏电阻在常温时的阻值,这样才能使变容二极管上的电压在高温时电压下降不多,低温时显著下降。考虑到热敏电阻的非线形和个体差异,使用的每一个热敏电阻都要测出其阻温曲线图。另外,基准电源是用稳压二极管稳压电路代替的,受温度影响基准电源也会有轻微变化,把以上变化综合考虑后代入专门的软件算出R1、R2、R3、R4、R5、R6、R8、R9的阻值。
实验结果与分析
变容二极管电路采用以上的温度补偿电路后,把调频电路后接电压放大和功率放大电路放入高低温箱观察,其试验数据见表。
表 变容二级管电路的频率随温度、时间变化的测量结果
温度(℃)/时间(min)
温度(℃)/时间(min)
| 15
| 30
| 45
| 60
|
-40
| 397.264kHz
| 397.265kHz
| 397.265kHz
| 397.265kHz
|
+25
| 397.265kHz
| 397.265kHz
| 397.265kHz
| 397.265kHz
|
+60
| 397.265kHz
| 397.265kHz
| 397.265kHz
| 397.266kHz
|
由于功放部分采用大功率三极管,整个电路本身发热严重,加上电路的耦合影响,对调频电路提出了更高的要求。从试验结果可以看出,低温时,频率在前15分钟有偏移,在高温时,后15分钟有偏移,这是正常的。在低温时,振荡器起振后,元器件参数随温度变化不稳定,工作10~15分钟后,电路将稳定下来。在高温后15分钟,由于大功率三极管发热严重,整个电路的温度上升很快,导致频率有轻微偏移。在高低温状态下,最大温度偏移小于0.001kHz,非常接近理论计算值。
结束语
理论上用本文提到的温度补偿法可以使载频保持不变,实验表明在低温的开始阶段和高温的最后阶段频率有偏移,如果使用两个热敏电阻补偿电路则可以使这两端的频率偏移消除,但是这种补偿电路的算法很复杂。在保证频率稳定度足够高的前提下,这一温度补偿法简洁、实用,在通信、电子产品有着广泛的应用前景。
引言
在变容二极管调频电路中,载频频率的不稳定性主要由温度变化、电源电压变化、负载阻抗变化等因素引起的。可以通过减少外界因素的变化来提高频率稳定度,如采用高稳定度直流稳压电源来减少电源电压的变化,采用金属屏蔽罩减少外界电磁场的变化,或者提高谐振回路的标准性,如采用参数稳定的回路电感器和电容器,采用温度补偿法,改进安装工艺,减弱振荡管与谐振回路的耦合。
在以上这些措施中,温度补偿法得到了广泛的应用。尤其是在军工产品方面,为了满足产品在高、低温环境下的工作性能要求,常常通过温度补偿法来减少温度对产品各项指标的影响。在变容二极管调频电路中,控制变容二极管的反向电压的轻微变动会导致频率偏移,在电路设计中,载频受温度变化的影响,通常规律是温度升高时频率变高,温度降低时载频瞬时起振频率偏低。如何兼顾高低温时的频率偏移,本文提供了一个简单的补偿电路,很好地解决了这个问题。

温度补偿的理论分析和模型
● 变容二极管调频电路的分析
变容二极管的调频电路如图1所示,在电路中,载频受温度的影响,通常规律是负的温度系数,即温度升高时频率变低,可以用具有负温度系数的电容来补偿。补偿用电容是C6、C12、C18,所用温度系数组别是C组。C9、C10、C11对失真度有较大的影响,可以选用一定温度系数电容来对失真度进行温度补偿,由于频率高、分散性大,没有较确切的规律可循,一般要靠试验确定,改变范围通常不宜过大,以调高或调低一挡为宜,个别电容可以改变到两挡。电感L2、L3、L4采用在高频陶瓷骨架上烧渗银制成的温度系数小、损耗小、Q值高的电感线圈,其Q值大于200,温度系数可达(1~5)×10-7/℃,防振性能好。另外还加了一个声表面波延迟线以对准频率,有时可能会产生自激,首先要找准自激发生在哪级,然后在该级回路中并以恰当的电阻。采用了以上措施,在常态下,调频电路的载频稳定度小于10-6。
一般情况下电感具有正温度系数,而电容根据不同介电材料,其温度系数可正可负。因此,选择合适的具有不同温度系数的电感和电容,同时接入谐振回路,从而使因温度变化引起的电感和电容值的变化互相抵消,使回路总电抗量变化减小。实际上,由于电感、电容大小随温度变化的非线性和晶体管极间电容和其他分布杂散电容的影响,在高低温时,频率的偏移往往较大。由此,考虑用可控制的电容变化抵消不确定的电感、电容变化。变容二极管上的电压包括直流电压和调制信号电压,通过控制直流电压即可达到目的。
● 温度补偿理论
要提高频率稳定度,回路的标准性越高越好。
设回路的总电感为L,总电容为C,回路的谐振频率为
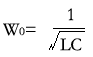
若温度变化引起L和C的微小变化分别为L和C,则W的变化量为
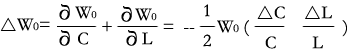
即
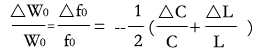
设电容量和电感量的相对变化值用βc和βl表示,则
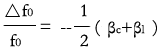
要提高频率稳定度,则必须是(βc+βl )的值越小越好,或者使βc、βl的数值符号相反,相互抵消。
在变容二极管调频电路中,变容二极管上的电压变化直接影响到频率的变化。通过电压控制电容的变化以抵消电感的变化。而变容二极管上的电压在不同温度状态下,差异很大。其电压—温度曲线如图2所示。


采用一般的电阻串、并联不能达到如此大的电压差异,需引入正温度系数(PTC)的热敏电阻。正温度系数热敏电阻材料主要有BaTiO3系陶瓷。BaTiO3热敏电阻器典型的阻温曲线如图3所示。可以看出,电阻率ρ首先随温度的升高而下降,当温度达到Tmin时,电阻率ρ达到最低值。之后ρ随T的升高而升高。当温度达到Tb以后,ρ随温度急剧升高,这一温度称为开关温度。温度为Tm时,电阻温度系数达到最大值,这时ρ与T几乎成直线关系。达到Tp之后,曲线弯曲,电阻温度系数迅速降低。当温度升高到Tmax之后,ρ重新随温度升高而降低。尤其要注意在居里温度以上,势垒急剧升高,电子跃迁变得困难,阻值剧增几个数量级以上的PTC现象。这时通过热敏电阻分压后到达变容二极管的电压会突然变小,因此设计中要消除或尽量减小PTC现象对电路的不良影响。通过合理的设计,即可使变容二极管上的电压在不同温度状态下都得到满足。
● 温度补偿的电路模型
综上所述,电路模型如图4所示。

在电路中,当温度升高,热敏电阻R7阻值变大。串并联电路(R5+R7)||R6的阻值变大,分压后加在变容二极管上的电压减小,当温度降低,(R5+R7)||R6的阻值变小,分压后加在变容二极管的电压增大。变容二极管上的电压变大变小的范围主要由R5、R6、R7调节,电阻R3、R4、R8、R9进行微调。一般情况下,R5、R6的阻值要小于热敏电阻在常温时的阻值,这样才能使变容二极管上的电压在高温时电压下降不多,低温时显著下降。考虑到热敏电阻的非线形和个体差异,使用的每一个热敏电阻都要测出其阻温曲线图。另外,基准电源是用稳压二极管稳压电路代替的,受温度影响基准电源也会有轻微变化,把以上变化综合考虑后代入专门的软件算出R1、R2、R3、R4、R5、R6、R8、R9的阻值。
实验结果与分析
变容二极管电路采用以上的温度补偿电路后,把调频电路后接电压放大和功率放大电路放入高低温箱观察,其试验数据见表。
表 变容二级管电路的频率随温度、时间变化的测量结果
温度(℃)/时间(min)
温度(℃)/时间(min)
| 15
| 30
| 45
| 60
|
-40
| 397.264kHz
| 397.265kHz
| 397.265kHz
| 397.265kHz
|
+25
| 397.265kHz
| 397.265kHz
| 397.265kHz
| 397.265kHz
|
+60
| 397.265kHz
| 397.265kHz
| 397.265kHz
| 397.266kHz
|
由于功放部分采用大功率三极管,整个电路本身发热严重,加上电路的耦合影响,对调频电路提出了更高的要求。从试验结果可以看出,低温时,频率在前15分钟有偏移,在高温时,后15分钟有偏移,这是正常的。在低温时,振荡器起振后,元器件参数随温度变化不稳定,工作10~15分钟后,电路将稳定下来。在高温后15分钟,由于大功率三极管发热严重,整个电路的温度上升很快,导致频率有轻微偏移。在高低温状态下,最大温度偏移小于0.001kHz,非常接近理论计算值。
结束语
理论上用本文提到的温度补偿法可以使载频保持不变,实验表明在低温的开始阶段和高温的最后阶段频率有偏移,如果使用两个热敏电阻补偿电路则可以使这两端的频率偏移消除,但是这种补偿电路的算法很复杂。在保证频率稳定度足够高的前提下,这一温度补偿法简洁、实用,在通信、电子产品有着广泛的应用前景。

 举报
举报


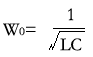
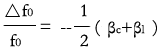




 举报
举报

