电力有源滤波器(APF)是颇受关注的用于谐波及无功功率补偿的装置。APF的补偿性能取决于主电路的拓扑结构和控制方式,APF主电路结构的研究已经比较成熟,目前实际应用的有源电力滤波器都是采用PWM变流器作为主电路,因此电力有源滤波器的性能依赖于所采用的控制方法。三相有源滤波技术得到了学者的普遍关注,提出了许多控制策略,但电力系统中存在着大量的单相负荷(如电气化铁道),这些负荷会造成电网的三相严重不平衡。目前单相有源滤波器的控制方法与三相有源滤波器的控制方法相比还不成熟。现有文献中单相有源滤波器的控制方法大都要进行谐波电流检测,然后根据谐波电流产生控制指令来控制主电路的开关动作,因此需要高精度的模拟乘法器或高速A/D、D/A以及DSP,电路结构复杂,参数灵敏度高;虽然也有一些不需要检测谐波电流和智能的控制方法相继提出,如单开关周期控制方法边带控制方法、神经网络控制方法等,但相比还不够成熟。
在数字控制技术获得广泛应用的今天,减少检测量、简化算法和实现易于数字化控制成为有源电力滤波器发展的方向。本文研究了单相有源电力滤波器、电源及非线性负载三者之间的能量交换机理,在此基础上得出了直流侧电容电压稳定调节的方法;提出了一种单相电压型有源滤波器的数字控制方法。该方法只需检测电源侧电流和变流器直流侧电容电压,据此实时计算各开关在每个开关周期内的占空比,形成开关的控制信号。计算机仿真结果验证了该方法的可行性。
1 直流侧电容电压的稳定调节
有源电力滤波器的作用就是使电源侧电流与电源电压同相并保持或接近正弦波形。在稳态情况下,对于一个无损的有源电力滤波系统,系统电源提供的能量必须等于负载消耗的功率,因此,变流器直流电容的平均电压将保持为一个定值。当功率不平衡时,如负载发生变化,变流器的直流电容将提供系统电源与负载间的功率差,这将导致直流电容平均电压的变化。如果系统电源提供的功率低于负载需要的功率,那么直流电容的平均电压将降低,此时,需要提高系统电流的幅值以增加系统电源提供的实功率;反之,直流电容平均电压将升高,此时,需要减小系统电流的幅值以降低系统提供的功率。直流侧电容平均电压的变化能够反映出主电路与负载间功率的转换情况。因此,期望的电源侧电流幅值可以通过直流侧电容电压调整获得。
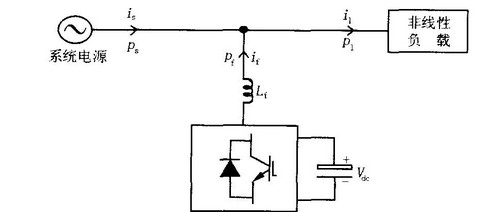
图1 电压型有源电力滤波器
电压型有源电力滤波器电路构成如图1所示,定义电网中电源传输的瞬时有功功率为Ps,负载侧传输的瞬时有功率为Pl,有源滤波器传输的瞬时有功功率为Pf。则在电源、负载和有源电力滤波器的公共交点处,电网中瞬时能量传输关系满足:

因此,它们的平均值Ps、Pl和Pf之间同样满足如下关系:

如果忽略有源电力滤波器本身的损耗,那么根据瞬时能量守恒,存在如下等式关系:
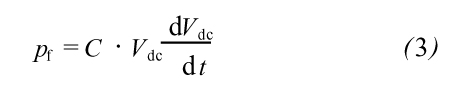
这里C为直流侧电容。由式(3)可计算有源滤波器传输的瞬时有功功率平均值Pf:

式中:T代表一个开关周期;Vdc(0)、Vdc(T)分别是0时刻和T时刻的直流侧电压;ΔV2dc是0时刻和T时
刻的直流侧电压的平方差。综合式(2)和式(4),有:
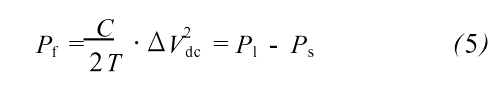
又因为电源侧平均功率为:

式中:Vs、Is分别是系统电源侧电压、电流的幅值。综合式(5)和式(6),得到Is的表达式:
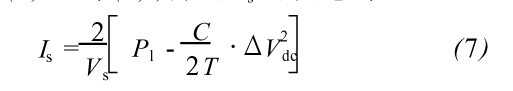
式(7)说明,如果Is不同于2/Vs*Pl时,直流侧电容电压将会有波动;Is可以由直流侧电容电压Vdc的变化量ΔVdc确定。
另外,为使有源电力滤波器正常工作,达到所要求的补偿效果,必须使直流侧电容电压Vdc维持足够高并且稳定,以保证在进行动态补偿的任何瞬间能根据控制要求输出所需的补偿电流;但由于补偿电流的时变性和变流器的自身损耗,如不采取适当的控制措施,直流侧电容电压Vdc将产生衰减或很大的波动,变流器不能正常运行。根据式(7),我们采用PI控制器将直流侧电容电压维持在要求的水平,将电容电压Vdc与设定的电压参考值Vref相比较,并将比较的结果ΔVdc送入PI控制器,PI控制器的输出就是电源侧电流期望的幅值Is,也即负载侧电流基波有功分量的幅值。
2 新型的数字控制方法
新型数字控制方法如图2所示。
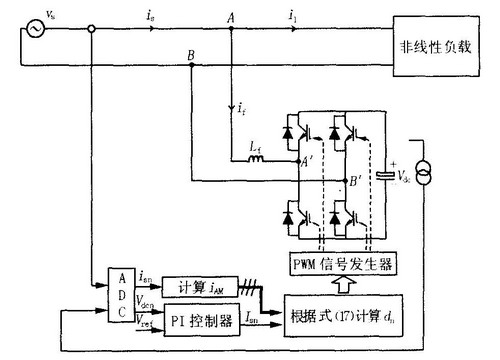
图2 单相电压型有源滤波器结构图
单相电压源型有源滤波器直流侧以电容作为储能元件来维持直流电压Vdc恒定。设开关周期恒定为T,第n个开关周期内占空比为dn,则这个开关周期内两对开关管分别导通的时间为dn*T和(1-dn)*T,从而分别可以得到两个电压平衡方程:
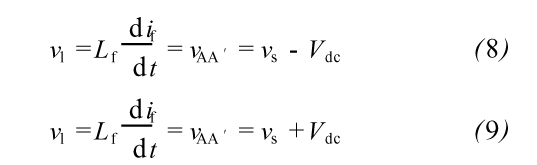
在稳定情况下,一个开关周期内电感上储存和释放的能量相等,即电感上的电流在第n个开关周期始末没变,所以:
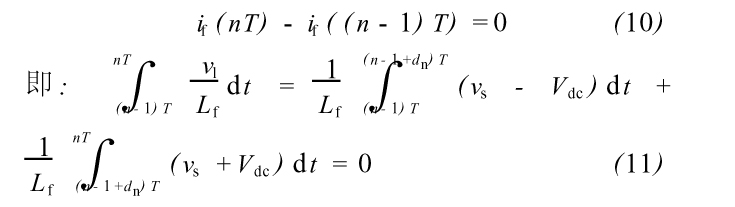
只要采样和开关的速度足够快,在一个开关周期内,我们可以认为vs、Vdc恒定,则式(11)可以化解为:

有源电力滤波器控制目标是使补偿后的电源侧电流为正弦且与电源电压同相,这样非线性负载和有源电力滤波器等效为一纯阻性负载Rs,即满足:

那么补偿后的电源侧电流幅值Is与电源电压幅值Vs存在如下关系:

稳定的直流侧电容Vdc电压与电源电压幅值Vs满足:

式中:K为比例系数,需根据补偿的要求选取合适的值(与电感、电容的参数也有关)。
将式(13)、(14)、(15)代入式(12)得到:

同样,只要采样和开关的速度足够快,is、Is在一个开关周期内可以近似认为是恒定的。则将式(16)离散化可得:
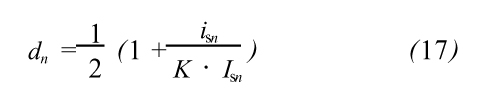
式中:dn为第n个开关周期的变流器的占空比;isn为第n个开关周期系统电源侧电流的采样值;Isn为第n个开关周期的PI控制器输出值。
基于式(17)可以实现有源滤波器的数字化控制,其基本结构如图2所示,在一个开关周期内控制器首先采样系统电流is和直流侧电容电压Vdc,经AD转换器转化为数字量isn、Vdcn,而Vdcn与直流电压Vref参考值经过数字PI调节器生成Isn,然后利用式(17)计算出桥臂开关的占空比dn送入PWM发生器,经驱动电路控制开关的动作。
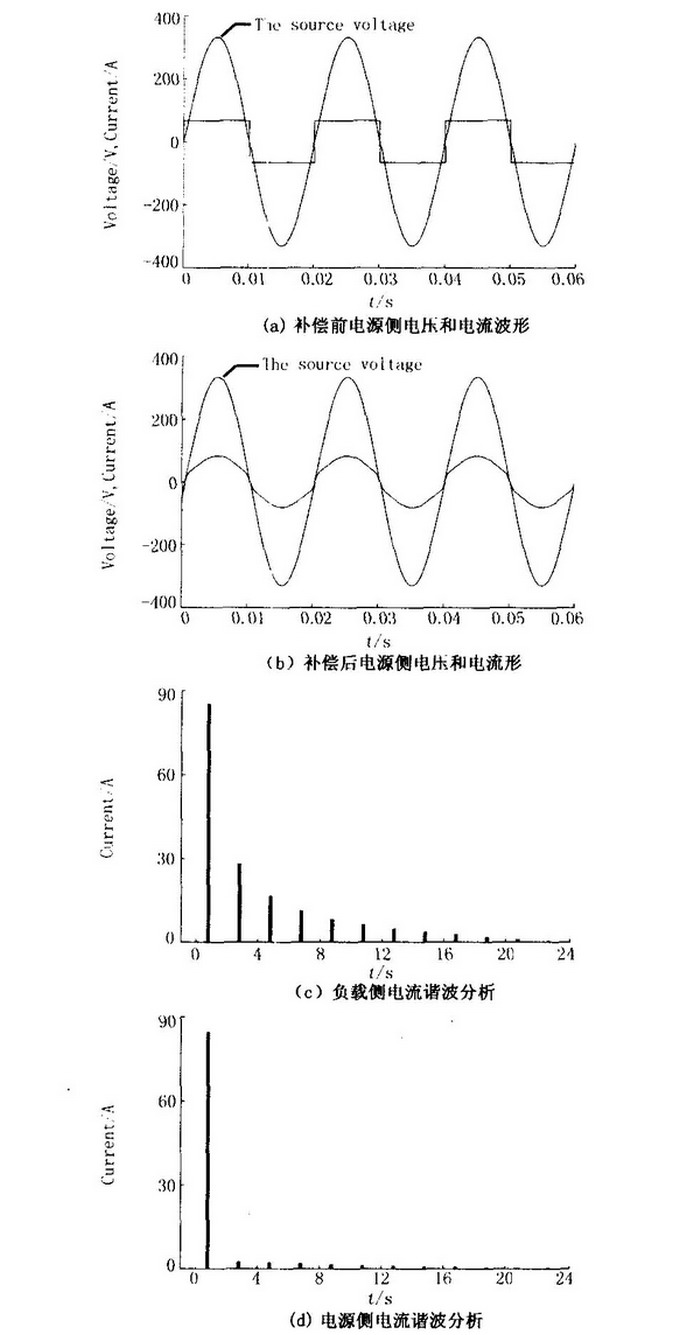
图3 谐波抑制仿真结果
3 仿真结果
图3给出了负载为非线性负载(带阻感负载的二极管整流桥)时,有源电力滤波器的工作情况。图3(a)是补偿前电源侧电压和电流波形,图3(c)是此时电流的谐波分析,3、5、7、11、13、15等次谐波很大;图3(b)是补偿后电源侧电压和电流波形,图3(d)是此时电流的谐波分析,3、5、7、11、13、15等次谐波得到明显的抑制。负载侧电流的THD为48.31%,电网侧电流的THD为6.52%。图4给出了负载为阻感负载时,有源电力滤波器的工作情况。图4(a)是补偿前电源侧电压和电流波形,图4(b)是补偿后电源侧电压和电流波形。补偿前电源侧系统的功率因数为0.6908,补偿后的功率因数为0.9988,实现了系统无功补偿和改善功率因数的目标。

图4 无功补偿仿真结果
4 结论
目前探索性能更好的新控制方法是有源电力滤波器研究的一个重要方向。本文提出的数字控制方法只需检测电源侧电流和变流器直流侧电容电压,据此实时计算各开关在每个开关周期内的占空比,形成开关的控制信号。该方法检测量少、算法简单、开关频率恒定、易于数字化实现。仿真结果表明,应用该方法的单相电压型有源电力滤波器能够有效地抑制谐波和补偿无功。不足之处在于PI参数的调节过于灵敏,实际应用中还有一定困难。
电力有源滤波器(APF)是颇受关注的用于谐波及无功功率补偿的装置。APF的补偿性能取决于主电路的拓扑结构和控制方式,APF主电路结构的研究已经比较成熟,目前实际应用的有源电力滤波器都是采用PWM变流器作为主电路,因此电力有源滤波器的性能依赖于所采用的控制方法。三相有源滤波技术得到了学者的普遍关注,提出了许多控制策略,但电力系统中存在着大量的单相负荷(如电气化铁道),这些负荷会造成电网的三相严重不平衡。目前单相有源滤波器的控制方法与三相有源滤波器的控制方法相比还不成熟。现有文献中单相有源滤波器的控制方法大都要进行谐波电流检测,然后根据谐波电流产生控制指令来控制主电路的开关动作,因此需要高精度的模拟乘法器或高速A/D、D/A以及DSP,电路结构复杂,参数灵敏度高;虽然也有一些不需要检测谐波电流和智能的控制方法相继提出,如单开关周期控制方法边带控制方法、神经网络控制方法等,但相比还不够成熟。
在数字控制技术获得广泛应用的今天,减少检测量、简化算法和实现易于数字化控制成为有源电力滤波器发展的方向。本文研究了单相有源电力滤波器、电源及非线性负载三者之间的能量交换机理,在此基础上得出了直流侧电容电压稳定调节的方法;提出了一种单相电压型有源滤波器的数字控制方法。该方法只需检测电源侧电流和变流器直流侧电容电压,据此实时计算各开关在每个开关周期内的占空比,形成开关的控制信号。计算机仿真结果验证了该方法的可行性。
1 直流侧电容电压的稳定调节
有源电力滤波器的作用就是使电源侧电流与电源电压同相并保持或接近正弦波形。在稳态情况下,对于一个无损的有源电力滤波系统,系统电源提供的能量必须等于负载消耗的功率,因此,变流器直流电容的平均电压将保持为一个定值。当功率不平衡时,如负载发生变化,变流器的直流电容将提供系统电源与负载间的功率差,这将导致直流电容平均电压的变化。如果系统电源提供的功率低于负载需要的功率,那么直流电容的平均电压将降低,此时,需要提高系统电流的幅值以增加系统电源提供的实功率;反之,直流电容平均电压将升高,此时,需要减小系统电流的幅值以降低系统提供的功率。直流侧电容平均电压的变化能够反映出主电路与负载间功率的转换情况。因此,期望的电源侧电流幅值可以通过直流侧电容电压调整获得。

图1 电压型有源电力滤波器
电压型有源电力滤波器电路构成如图1所示,定义电网中电源传输的瞬时有功功率为Ps,负载侧传输的瞬时有功率为Pl,有源滤波器传输的瞬时有功功率为Pf。则在电源、负载和有源电力滤波器的公共交点处,电网中瞬时能量传输关系满足:

因此,它们的平均值Ps、Pl和Pf之间同样满足如下关系:

如果忽略有源电力滤波器本身的损耗,那么根据瞬时能量守恒,存在如下等式关系:
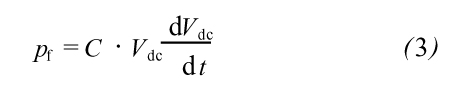
这里C为直流侧电容。由式(3)可计算有源滤波器传输的瞬时有功功率平均值Pf:

式中:T代表一个开关周期;Vdc(0)、Vdc(T)分别是0时刻和T时刻的直流侧电压;ΔV2dc是0时刻和T时
刻的直流侧电压的平方差。综合式(2)和式(4),有:
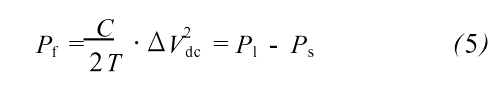
又因为电源侧平均功率为:

式中:Vs、Is分别是系统电源侧电压、电流的幅值。综合式(5)和式(6),得到Is的表达式:
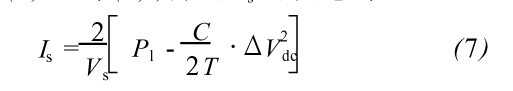
式(7)说明,如果Is不同于2/Vs*Pl时,直流侧电容电压将会有波动;Is可以由直流侧电容电压Vdc的变化量ΔVdc确定。
另外,为使有源电力滤波器正常工作,达到所要求的补偿效果,必须使直流侧电容电压Vdc维持足够高并且稳定,以保证在进行动态补偿的任何瞬间能根据控制要求输出所需的补偿电流;但由于补偿电流的时变性和变流器的自身损耗,如不采取适当的控制措施,直流侧电容电压Vdc将产生衰减或很大的波动,变流器不能正常运行。根据式(7),我们采用PI控制器将直流侧电容电压维持在要求的水平,将电容电压Vdc与设定的电压参考值Vref相比较,并将比较的结果ΔVdc送入PI控制器,PI控制器的输出就是电源侧电流期望的幅值Is,也即负载侧电流基波有功分量的幅值。
2 新型的数字控制方法
新型数字控制方法如图2所示。

图2 单相电压型有源滤波器结构图
单相电压源型有源滤波器直流侧以电容作为储能元件来维持直流电压Vdc恒定。设开关周期恒定为T,第n个开关周期内占空比为dn,则这个开关周期内两对开关管分别导通的时间为dn*T和(1-dn)*T,从而分别可以得到两个电压平衡方程:
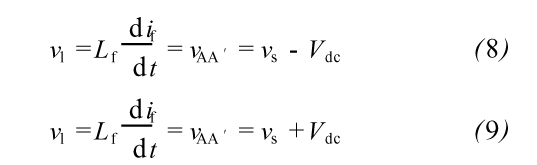
在稳定情况下,一个开关周期内电感上储存和释放的能量相等,即电感上的电流在第n个开关周期始末没变,所以:
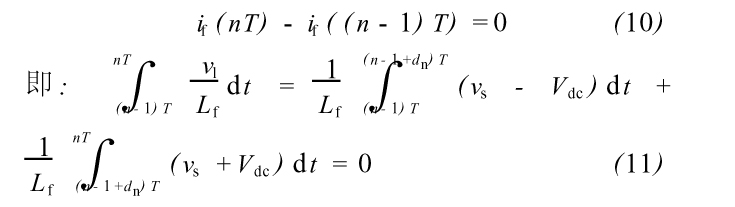
只要采样和开关的速度足够快,在一个开关周期内,我们可以认为vs、Vdc恒定,则式(11)可以化解为:

有源电力滤波器控制目标是使补偿后的电源侧电流为正弦且与电源电压同相,这样非线性负载和有源电力滤波器等效为一纯阻性负载Rs,即满足:

那么补偿后的电源侧电流幅值Is与电源电压幅值Vs存在如下关系:

稳定的直流侧电容Vdc电压与电源电压幅值Vs满足:

式中:K为比例系数,需根据补偿的要求选取合适的值(与电感、电容的参数也有关)。
将式(13)、(14)、(15)代入式(12)得到:

同样,只要采样和开关的速度足够快,is、Is在一个开关周期内可以近似认为是恒定的。则将式(16)离散化可得:
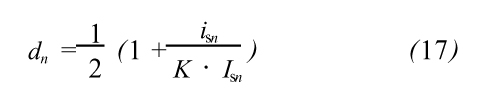
式中:dn为第n个开关周期的变流器的占空比;isn为第n个开关周期系统电源侧电流的采样值;Isn为第n个开关周期的PI控制器输出值。
基于式(17)可以实现有源滤波器的数字化控制,其基本结构如图2所示,在一个开关周期内控制器首先采样系统电流is和直流侧电容电压Vdc,经AD转换器转化为数字量isn、Vdcn,而Vdcn与直流电压Vref参考值经过数字PI调节器生成Isn,然后利用式(17)计算出桥臂开关的占空比dn送入PWM发生器,经驱动电路控制开关的动作。

图3 谐波抑制仿真结果
3 仿真结果
图3给出了负载为非线性负载(带阻感负载的二极管整流桥)时,有源电力滤波器的工作情况。图3(a)是补偿前电源侧电压和电流波形,图3(c)是此时电流的谐波分析,3、5、7、11、13、15等次谐波很大;图3(b)是补偿后电源侧电压和电流波形,图3(d)是此时电流的谐波分析,3、5、7、11、13、15等次谐波得到明显的抑制。负载侧电流的THD为48.31%,电网侧电流的THD为6.52%。图4给出了负载为阻感负载时,有源电力滤波器的工作情况。图4(a)是补偿前电源侧电压和电流波形,图4(b)是补偿后电源侧电压和电流波形。补偿前电源侧系统的功率因数为0.6908,补偿后的功率因数为0.9988,实现了系统无功补偿和改善功率因数的目标。

图4 无功补偿仿真结果
4 结论
目前探索性能更好的新控制方法是有源电力滤波器研究的一个重要方向。本文提出的数字控制方法只需检测电源侧电流和变流器直流侧电容电压,据此实时计算各开关在每个开关周期内的占空比,形成开关的控制信号。该方法检测量少、算法简单、开关频率恒定、易于数字化实现。仿真结果表明,应用该方法的单相电压型有源电力滤波器能够有效地抑制谐波和补偿无功。不足之处在于PI参数的调节过于灵敏,实际应用中还有一定困难。

 举报
举报




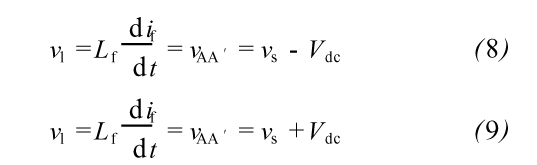
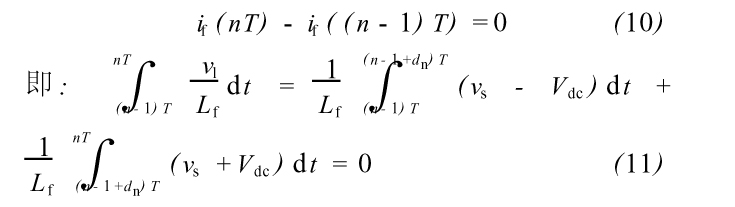



 举报
举报

