分立元件VCO能够提供足够的自由度来满足大多数系统的性能要求(调谐范围、输出功率、相位噪声、电流消耗等等)。然而,对于具有较大批量、价格敏感的现代产品,振荡频率的生产线调整是不可接受的。这迫使射频工程师必须设计出一个不需要在安装过程中调整的VCO,即免调节VCO。这项设计任务并不简单,除了要掌握VCO的基本设计原理外,还需要射频工程师花费大量精力来保证设计的一致性,而且在各种因素(如元件参数、温度及电源电压等)允许的变化范围内,振荡器始终调谐在正确的频率。本文试图对这项任务的重要性给出一个评价,同时解释一些和免调节中频VCO设计有关的问题。 VCO结构 ----有多种可行的振荡器结构都可用于构建一个实用的射频VCO,其中一种已经在许多商品化VCO模块和不计其数的分立VCO电路中得到了成功应用,这就是Colpitts共集电极电路(图1)。该结构可用于很宽的工作频率范围,从中频直到射频。

图1:基本Colpitts振荡器
灵活、廉价、并具有足够高性能的VCO可基于一个由廉价的表贴电感和变容二极管组成的电感-电容(LC)谐振槽路组成。振荡器槽路是一个并联谐振电路,控制着振荡频率,电感或电容的任何变化都会改变振荡频率。电感和压变电容能够以并联或串联模式的网络形式实现可变谐振。并联模式网络(图2)可用于较低频率,因为大值压变电容难以实现而电感可以做得比较大。并联模式配置还使于对振荡器做直观地分析。

图2:Colpitts结构用于VCO
对于Colpitts振荡器可以采用一种简化的、精确性稍差的方法来加以分析,并得到一组更清晰、更直观的设计方程,有助于一阶振荡器的设计。首先,Colpitts振荡器可重画为一个带有正反馈的LC放大器(图3)。这个视点易于计算环路增益、振荡幅度和相位噪声。为了描述启动过程和振荡频率,最初的电路也可重画为一个负阻加谐振器结构(图4)。从上述两个视点得到的一系列方程联合起来构成一组Colpitts振荡器的设计方程(Meyer 1998)。
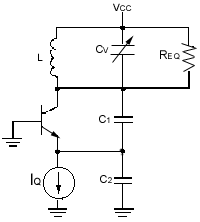
图3:LC放大器模型

图4:映像放大器模型
Colpitts振荡器的基本设计方程
在图2中,不考虑分布参数,并假定CC》》C1和C2,并有C1》Cπ(Cπ为三极管基-射结电容)。振荡频率可按下式计算:
f0=1/(2π√(L*CT)), CT=CV+C12.。。。。。。。。。。。。。。。。。。。。。。。。。。(1)
CV=(CVAR*C0)/(CVAR+C0), C12=(C1*C2)/(C1+C2)
谐振电路的品质因数(QT)可按下式计算:
QV≌1/(2π*CV*RS*F0), RQC=QV2*RS.。。。。。。。。。。。。。。。。。。。。。。。。。(2)
QT≌REQ/(2π*L*F0), REQ=RQL‖RQC
振荡幅度可按下式估算:
V0=2*IQ*REQ*(J1(β)/J0(β)), V0=IQ*REQ*1.4.。。。。。。。。。。。。(3)
环路增益和起振条件按下式计算:
环路增益=gm*REQ*1/n, 当n=(C1+C2)/C2.。。。。。。。。。。。。。。。。。。。。。。(4)
起振条件:
gm/((2π*C1*f0)(2π*C2*f0))》》(REQ/QT2)。。。。。。。。。。。。。。。。。。。。(5)
距离中心频率一定频偏(fm)处Colpitts振荡器的相位噪声(PN)可按下式计算:
PN=in2*(1/V02)*[f0/(2Q0)]2*(REQ2/fm)。。。。。。。。。。。。。。。。。。。。。(6)
上述公式中:Co=压变电容耦合电容:CT=总谐振电容;CVAR=压变电容;fm=以Hz为单位的相位噪声频偏;fo=振荡频率;gm=双极晶体管跨导;in=集电结散粒噪声;IQ=振荡晶体管偏流;QL=电感Q;QT=谐振电路Q;QV=等效压变电容Q;REQ=谐振电路等效并联电阻;RS=压变电容串联电阻; VO=谐振电压均方根值。 免调节VCO的设计考虑
免调节VCO从概念上讲非常简单。只要振荡器具有足够宽裕的调谐范围来消除所有的误差源(如元件容差)所引起的频率偏移,振荡频率的调整就可以省去。初看起来,这项任务非常简单明了,只需提供足够的调谐范围来覆盖所有的误差源即可。然而,对于一个给定的调谐电压范围,有限的可变电容限制了频率调谐范围,而且,VCO的电性能要求往往进一步将调谐范围限制在更窄的区间内。另外,过大的调谐范围还会给振荡器带来一些负面影响。很宽的调谐范围要求压变电容至槽路间有很重的容性耦合,这会严重降低谐振电路的品质因数Q。所带来的结果便是更大的相位噪声、对调谐线噪声更为敏感、压变电容两端过大的电压摆幅、潜在的启动问题等,并给环路滤波器设计带来很大的困难。
较宽的调谐范围可通过两个容易理解的途径增大振荡器的相位噪声:降低谐振电路Q值和调谐线噪声的影响。要获得更宽的调谐范围,压变电容必须通过一个更大的电容耦合到谐振电路。这会降低CV(等效可变电容)的Q值,如方程(2)所示。CV的Q值降低同时使谐振电路净Q值也降低,因而导致相位噪声增加,如方程(6)所示。致使相位噪声增加的第二个因素是调谐输入端的热噪声,它会产生频率调制的边带噪声。该项噪声随着调谐范围而增加,并有可能超过振荡器的固有相位噪声。由热噪声引起的相位噪声可由下式计算:
PN=201og[√2*KV*Vn/(2*fm)],
Kv=VCO增益(Hz/V),Vn=噪声密度(V/√(Hz)。。。。。。。。。。。。。。。。。。。。。。。。。(7)
显然,两种情况的相位噪声都随着调谐范围的增加而增大。因此要便免调节VCO保持较低的相位噪声,至关重要的是设定一个恰当的调谐范围,保证带宽要求并能容纳各种可预见的误差源。由于压变电容耦合的加重,更多的谐振电压摆幅会出现在压变电容两端,而压变电容电压的摆幅必须加以限制以防压变电容被正向偏置。这就限制了谐振电路中的信号功率,因而也就影响到振荡器的相位噪声。最后,当谐振电路的等效串联电阻过大时还会带来起振问题(参见基本方程)。频率调谐范围过宽的VCO可能无法正常起振,尤其是在极限温度下。那么,要实现恰当的调谐范围,首先碰到的问题就是确定恰当的调谐范围。 影响振荡率的误差源
为了适应影响振荡频率的各种误差源,免调节VCO的频率调谐范围必须增加。这些误差源可分为两类:元件参数误差和设计对准误差。设定振荡频率的LC元件当然是非理想的,它们会带来以下问题:
元件之间的差异(容差);
不理想的性能(由于电感、电容以及引线串联电阻等造成有限的频率响应);
电路布线中的分布电容和电感造成的误差。
附表列出了振荡器中频率设定元件的典型容差。另一方面,设计过程中在对准VCO调谐范围时的不确定因素还会导致设计对准误差。设计对准作为一个振荡频率建立中的误差来源常常被忽视。为了充分利用现有的频率调谐范围,调谐边界必须相对于预期的振荡频率相对称。在建立这个中心点时的任何误差,主要是由元件模型的初始值或平均值的不精确性而引起,都会降低可用的调谐范围。为了在各种温度、电源电压、元件容差等条件下保证振荡频率,调谐范围必须足够宽,以便容纳该误差。可以利用振荡频率公式计算出总的频率误差,只需对其中的每项元素乘以一个比例因子即可。
附表振荡器中频率设定元件的典型容差
元件容差
压变电容±15%于VTUNE=0.4V
±10%于VTUNE=2.4V
电感±5%
电容±5%
分布电容±10%
分布电感±6%
振荡元件阻抗±15%
频率偏移和调谐范围
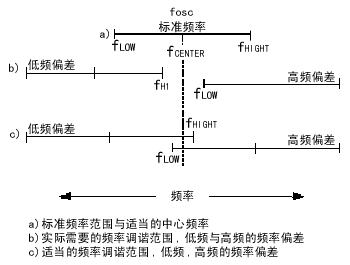
频率调谐范围可通过改变调谐电压获得,从VTUNE(LOW)到VTUNE(HIGH),具有高、低频率边界(fHIGH和flow)和一个位于fHIGH和fLOW中点的“中心”频率(fcenter)(图5)。理想情况下,调谐范围应安排在使fCENTER恰好位于期望频率的位置(图5a)。然而,元件误差和设计对准误差可能会使频率调谐区间发生偏移。如果在最差情况下,系统提供的调谐电压不足,不能获得足够的频率调谐范围,则期望的振荡频率就无法达到(图5b)。显然,仔细确定调谐范围需求是很有必要的。这可能过以下方法实现,首先计算出所有误差源所引起的频率偏差,然后确定最差情况下的fLOWfOSC且fHIGH》fOSC(图5c)。
设计验证
线路板布局和元件选择完成之后,还需要对设计进行验证和测试。通常,必须检查调谐范围、启动性能、相位噪声等等性能是否符合设计要求。此外,测试必须基于一个统计有效的生产流程数量之上,以使确定调谐范围和平均中心频率,以及它们相对于预期振荡频率的相对位置。所有这些工作都是得到一个稳定的、可重复生产并具有预期性能的设计所必需的。Maxim公司已开发出新款VCO IC MAX2620,解决了VCO的设计难题,同时显著缩短了实现免调节中频VCO所必需的时间。
分立元件VCO能够提供足够的自由度来满足大多数系统的性能要求(调谐范围、输出功率、相位噪声、电流消耗等等)。然而,对于具有较大批量、价格敏感的现代产品,振荡频率的生产线调整是不可接受的。这迫使射频工程师必须设计出一个不需要在安装过程中调整的VCO,即免调节VCO。这项设计任务并不简单,除了要掌握VCO的基本设计原理外,还需要射频工程师花费大量精力来保证设计的一致性,而且在各种因素(如元件参数、温度及电源电压等)允许的变化范围内,振荡器始终调谐在正确的频率。本文试图对这项任务的重要性给出一个评价,同时解释一些和免调节中频VCO设计有关的问题。 VCO结构 ----有多种可行的振荡器结构都可用于构建一个实用的射频VCO,其中一种已经在许多商品化VCO模块和不计其数的分立VCO电路中得到了成功应用,这就是Colpitts共集电极电路(图1)。该结构可用于很宽的工作频率范围,从中频直到射频。

图1:基本Colpitts振荡器
灵活、廉价、并具有足够高性能的VCO可基于一个由廉价的表贴电感和变容二极管组成的电感-电容(LC)谐振槽路组成。振荡器槽路是一个并联谐振电路,控制着振荡频率,电感或电容的任何变化都会改变振荡频率。电感和压变电容能够以并联或串联模式的网络形式实现可变谐振。并联模式网络(图2)可用于较低频率,因为大值压变电容难以实现而电感可以做得比较大。并联模式配置还使于对振荡器做直观地分析。

图2:Colpitts结构用于VCO
对于Colpitts振荡器可以采用一种简化的、精确性稍差的方法来加以分析,并得到一组更清晰、更直观的设计方程,有助于一阶振荡器的设计。首先,Colpitts振荡器可重画为一个带有正反馈的LC放大器(图3)。这个视点易于计算环路增益、振荡幅度和相位噪声。为了描述启动过程和振荡频率,最初的电路也可重画为一个负阻加谐振器结构(图4)。从上述两个视点得到的一系列方程联合起来构成一组Colpitts振荡器的设计方程(Meyer 1998)。

图3:LC放大器模型

图4:映像放大器模型
Colpitts振荡器的基本设计方程
在图2中,不考虑分布参数,并假定CC》》C1和C2,并有C1》Cπ(Cπ为三极管基-射结电容)。振荡频率可按下式计算:
f0=1/(2π√(L*CT)), CT=CV+C12.。。。。。。。。。。。。。。。。。。。。。。。。。。(1)
CV=(CVAR*C0)/(CVAR+C0), C12=(C1*C2)/(C1+C2)
谐振电路的品质因数(QT)可按下式计算:
QV≌1/(2π*CV*RS*F0), RQC=QV2*RS.。。。。。。。。。。。。。。。。。。。。。。。。。(2)
QT≌REQ/(2π*L*F0), REQ=RQL‖RQC
振荡幅度可按下式估算:
V0=2*IQ*REQ*(J1(β)/J0(β)), V0=IQ*REQ*1.4.。。。。。。。。。。。。(3)
环路增益和起振条件按下式计算:
环路增益=gm*REQ*1/n, 当n=(C1+C2)/C2.。。。。。。。。。。。。。。。。。。。。。。(4)
起振条件:
gm/((2π*C1*f0)(2π*C2*f0))》》(REQ/QT2)。。。。。。。。。。。。。。。。。。。。(5)
距离中心频率一定频偏(fm)处Colpitts振荡器的相位噪声(PN)可按下式计算:
PN=in2*(1/V02)*[f0/(2Q0)]2*(REQ2/fm)。。。。。。。。。。。。。。。。。。。。。(6)
上述公式中:Co=压变电容耦合电容:CT=总谐振电容;CVAR=压变电容;fm=以Hz为单位的相位噪声频偏;fo=振荡频率;gm=双极晶体管跨导;in=集电结散粒噪声;IQ=振荡晶体管偏流;QL=电感Q;QT=谐振电路Q;QV=等效压变电容Q;REQ=谐振电路等效并联电阻;RS=压变电容串联电阻; VO=谐振电压均方根值。 免调节VCO的设计考虑
免调节VCO从概念上讲非常简单。只要振荡器具有足够宽裕的调谐范围来消除所有的误差源(如元件容差)所引起的频率偏移,振荡频率的调整就可以省去。初看起来,这项任务非常简单明了,只需提供足够的调谐范围来覆盖所有的误差源即可。然而,对于一个给定的调谐电压范围,有限的可变电容限制了频率调谐范围,而且,VCO的电性能要求往往进一步将调谐范围限制在更窄的区间内。另外,过大的调谐范围还会给振荡器带来一些负面影响。很宽的调谐范围要求压变电容至槽路间有很重的容性耦合,这会严重降低谐振电路的品质因数Q。所带来的结果便是更大的相位噪声、对调谐线噪声更为敏感、压变电容两端过大的电压摆幅、潜在的启动问题等,并给环路滤波器设计带来很大的困难。
较宽的调谐范围可通过两个容易理解的途径增大振荡器的相位噪声:降低谐振电路Q值和调谐线噪声的影响。要获得更宽的调谐范围,压变电容必须通过一个更大的电容耦合到谐振电路。这会降低CV(等效可变电容)的Q值,如方程(2)所示。CV的Q值降低同时使谐振电路净Q值也降低,因而导致相位噪声增加,如方程(6)所示。致使相位噪声增加的第二个因素是调谐输入端的热噪声,它会产生频率调制的边带噪声。该项噪声随着调谐范围而增加,并有可能超过振荡器的固有相位噪声。由热噪声引起的相位噪声可由下式计算:
PN=201og[√2*KV*Vn/(2*fm)],
Kv=VCO增益(Hz/V),Vn=噪声密度(V/√(Hz)。。。。。。。。。。。。。。。。。。。。。。。。。(7)
显然,两种情况的相位噪声都随着调谐范围的增加而增大。因此要便免调节VCO保持较低的相位噪声,至关重要的是设定一个恰当的调谐范围,保证带宽要求并能容纳各种可预见的误差源。由于压变电容耦合的加重,更多的谐振电压摆幅会出现在压变电容两端,而压变电容电压的摆幅必须加以限制以防压变电容被正向偏置。这就限制了谐振电路中的信号功率,因而也就影响到振荡器的相位噪声。最后,当谐振电路的等效串联电阻过大时还会带来起振问题(参见基本方程)。频率调谐范围过宽的VCO可能无法正常起振,尤其是在极限温度下。那么,要实现恰当的调谐范围,首先碰到的问题就是确定恰当的调谐范围。 影响振荡率的误差源
为了适应影响振荡频率的各种误差源,免调节VCO的频率调谐范围必须增加。这些误差源可分为两类:元件参数误差和设计对准误差。设定振荡频率的LC元件当然是非理想的,它们会带来以下问题:
元件之间的差异(容差);
不理想的性能(由于电感、电容以及引线串联电阻等造成有限的频率响应);
电路布线中的分布电容和电感造成的误差。
附表列出了振荡器中频率设定元件的典型容差。另一方面,设计过程中在对准VCO调谐范围时的不确定因素还会导致设计对准误差。设计对准作为一个振荡频率建立中的误差来源常常被忽视。为了充分利用现有的频率调谐范围,调谐边界必须相对于预期的振荡频率相对称。在建立这个中心点时的任何误差,主要是由元件模型的初始值或平均值的不精确性而引起,都会降低可用的调谐范围。为了在各种温度、电源电压、元件容差等条件下保证振荡频率,调谐范围必须足够宽,以便容纳该误差。可以利用振荡频率公式计算出总的频率误差,只需对其中的每项元素乘以一个比例因子即可。
附表振荡器中频率设定元件的典型容差
元件容差
压变电容±15%于VTUNE=0.4V
±10%于VTUNE=2.4V
电感±5%
电容±5%
分布电容±10%
分布电感±6%
振荡元件阻抗±15%
频率偏移和调谐范围
频率调谐范围可通过改变调谐电压获得,从VTUNE(LOW)到VTUNE(HIGH),具有高、低频率边界(fHIGH和flow)和一个位于fHIGH和fLOW中点的“中心”频率(fcenter)(图5)。理想情况下,调谐范围应安排在使fCENTER恰好位于期望频率的位置(图5a)。然而,元件误差和设计对准误差可能会使频率调谐区间发生偏移。如果在最差情况下,系统提供的调谐电压不足,不能获得足够的频率调谐范围,则期望的振荡频率就无法达到(图5b)。显然,仔细确定调谐范围需求是很有必要的。这可能过以下方法实现,首先计算出所有误差源所引起的频率偏差,然后确定最差情况下的fLOWfOSC且fHIGH》fOSC(图5c)。

设计验证
线路板布局和元件选择完成之后,还需要对设计进行验证和测试。通常,必须检查调谐范围、启动性能、相位噪声等等性能是否符合设计要求。此外,测试必须基于一个统计有效的生产流程数量之上,以使确定调谐范围和平均中心频率,以及它们相对于预期振荡频率的相对位置。所有这些工作都是得到一个稳定的、可重复生产并具有预期性能的设计所必需的。Maxim公司已开发出新款VCO IC MAX2620,解决了VCO的设计难题,同时显著缩短了实现免调节中频VCO所必需的时间。

 举报
举报







 举报
举报

