1 引 言
时域有限差分法(Fnite Difference Time Domain,FDTD)是1966年K.S.Yee首先提出的一种以Maxwell方程为基础的解决电磁场问题的数值计算方法。FDTD算法将Maxwell方程中的两个旋度方程直接转化为差分形式,将电磁场进行空间和时问上的离散化,得到电磁场演化的迭代方程组,实现在一定体积内和一段时间上对连续电磁场的数据取样压缩。
应用FDTD算法对某一个具体的目标进行电磁仿真时,要将目标分解和描述成FDTD仿真软件可以处理的数据格式。在运用FDTD算法早期,由于受计算资源和图形显示设备的局限,用于仿真的建模数据多采用文本编辑形式,对于较复杂物体,很难及时发现建模过程中出现的错误,这种错误将被延续到仿真过程中,而专门的可视化建模模块可以使建模的效率和准确性得到提高。为了使仿真程序具有在不同操作系统的通用性,将电磁学模拟软件分为建模及结果处理模块、仿真模块两个部分,建模及结果处理模块专门进行目标物体的几何和电磁学参数的预设及相关数据的预处理,对模拟结果进行可视化显示;仿真模块专门对建模生成的数据文件进行相应的FDTD电磁模拟。
最后,以具体实例展现该建模模块的可视化效果、友好的图形化界面、结果的精确性和可靠性。
2 建模算法
2.1建模物体的描述
对目标物体进行电磁学建模就是对目标物体的介质参数、几何参数、边界条件、激励源、输出记录等问题的描 述过程,并进行数据的预处理,生成仿真模块处理所需的数据文件。
(1)首先将建模目标物体中使用到的介质参数进行编号并生成介质列表。
(2)然后对目标物体进行几何参数设定,根据FDTD算法和目标物体自身结构特点,在直角坐标系下将物体分解单个矩形块输入。几何参数的输入有两种方式,一种是预先规定各个方向单个网格的尺寸,输入矩形的坐标以网格为单位;另一种是直接输入目标分解的矩形块的实际尺寸。两种情况都要给出矩形区域的介质编号。
(3)对目标物体根据具体问题对计算空间边界选择相应的边界条件,有一阶和二阶Mur、一阶和二阶Dispersive,PMC,PEC,PML等7种边界条件供选择。
(4)目标物体激励源的设定,建模软件激励源采用软激励形式,将激励源信号加在目标物体网格坐标上。在完成上述工作以后,指定用于记录输出的网格坐标,用于记录仿真数据。
2.2 非均匀网格划分算法
为FDTD仿真程序提供尺寸合适的均匀和非均匀网格是建模的重要任务,在物体边界电磁场变化较大的地方宜采用细网格,而在物体边界电磁场变化比较小的地方宜采用粗网格;考虑算法的数值色散的影响,任一网格的尺寸δ≤λmin/12,λmin为关心的上限频率所对应的波长。为了节约计算资源和提高工作效率,对一些较复杂的目标物体采用非均匀网格划分方式。非均匀网格的划分遵守下列规则:
(1)目标物体任一子区域的边界在网格线上。
(2)在各个方向上任意两个相邻网格尺寸比值≤1.25。
进行非均匀网格划分,根据网格密度分布方式有:“密→疏”、“疏→密”、“密→疏→密”等3种分布方式。这里将盼“密→疏→密”非均匀网格为例介绍网格划分算法。
将目标物体在各个方向的几何参数排序划分成若干不重复的子区域,然后在各个子区按上述网格划分规则进行划分。在该模块中,用户可以预先设定3个方向中各个方向最大网格尺寸、最小网格尺寸和相邻网格尺寸比例,然后系统对3个方向网格进行一次性划分,并对网格划分进行规则检测,对用户进行提示,然后用户可以根据各个子区域情况进行优化。这里以X方向上某一子区域上进行网格划分为例来说明。设X方向某个子区域的长度为L,X方向最小的网格尺寸为Xmin,X方向最大网格尺寸Xmax,X方向预设相邻网格比例R∈[1,1.25]。网格的尺寸由区域的一边向中间逐渐增大,然后向另一边逐渐减小。
取该区域长度的一半L/2,令△x=Xmin,由:
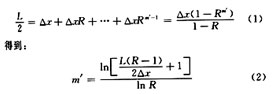
式(2)可能得到的不是一个整数,m′取整INT(m′),将m 代入△xRm-1,考虑下面两种情形:
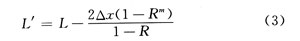
(1)假如△xRm-1≤Xmax令
取K=min{△xRm,Xmax}考虑几种情况:
①若L'≥1.5K,将L'均分为2个网格;
②若1.5K》L'≥K,则L'=K+△L',调整R使△L'=0:
③若L'这样在①条件下生成2m+2个网格,②条件下生成2m+1个网格,③条件下生成2m个网格。
(2)假如△xRm-1》Xmax,找出n1的值,满足,△xRn1-13建模模块及结果处理模块实现
在基于上述非均匀网格划分算法和计算机图形学基础上,我们设计出了可以实现三维复杂物体建模和图形处理的建模可视化模块,可一次性生成仿真软件所需的网格、电磁参数、边界条件和激励源设置等数据文件,可实时实现对数据的监控和修改,实现了对仿真结果的可视化显示。
本文介绍的建模模块可对微带线、微带滤波器、微带电感、贴片天线等无源器件及设备进行建模和分析,实现对目标物体进行二维和三维观察。实现目标物体水平移动、三维转动和放大,并可在网格划分后对划分效果进行二维和三维的观察。图1所示是使用该可视化模块对目标物体建模得到的三维网格图。
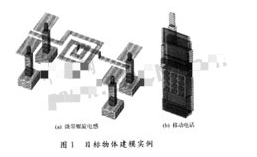
4 目标物体建模及模拟结果可视化应用实例
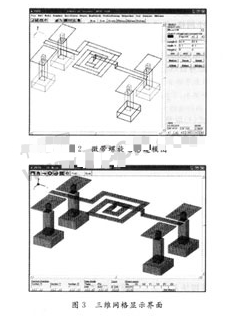
下面将以微带螺旋电感Ⅲ(如图2和图3所示)为例介绍应用该建模模块进行目标物体建模,在模拟以后对模拟结果进行可视化展示。
4.1 目标物体建模
4.1.1 目标物体几何参数及电磁参数输入
首先,根据螺旋电感的实际尺寸确定计算空间的大小,由于网格划分要遍布整个计算空间,为了节约计算资源,保证对螺旋电感的模拟精度,计算空间的范围应大小适中。然后,将螺旋电感分解成若干矩形块,按顺序输入各个矩形块的型值点和材料参数。
4.1.2 网格划分和激励源设置
在输入螺旋电感的几何和材料参数输入完成并检查确定无误的情况下,可以对目标物体在整个计算空间内进行网格划分。然后通过系统检查,对错误的子区域给出标记,建议修改。在完成各子区域内的修改后显示整个计算区域网格的分布。在完成网格划分后,加入激励源。
在完成建模后,调用自行研制的FDTD仿真模块进行运算,输出指定坐标的仿真结果。据此提取的微带螺旋电感特性参数结果一致。
4.2结果可视化
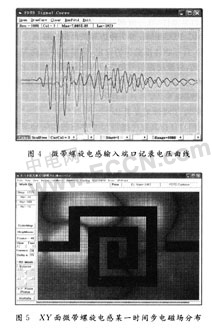
将仿真数据结果处理,在信号处理界面用图表曲线形式来显示出来,螺旋电感输入端口记录电压如图4所示。为直观地表现物理过程,电磁场分布显示界面可以用动画形式显示电磁场随时间步变化演变过程。图5为截取XY面螺旋电感电磁场演变动画中的一幅。
5 结 语
我们研究、设计了用于FDTD仿真软件的电磁建模模块,经过多次建模和模拟实验测试,表明对目标物体建模效率高,生成网格坐标和相关数据准确、高效,建模可视化效果好,对建模目标实现三维多角度实时观察和调整,并且界面友好、操作简单,显著提高了建模的工作效率,进而提高了应用FDTD算法解决具体问题的效率。
1 引 言
时域有限差分法(Fnite Difference Time Domain,FDTD)是1966年K.S.Yee首先提出的一种以Maxwell方程为基础的解决电磁场问题的数值计算方法。FDTD算法将Maxwell方程中的两个旋度方程直接转化为差分形式,将电磁场进行空间和时问上的离散化,得到电磁场演化的迭代方程组,实现在一定体积内和一段时间上对连续电磁场的数据取样压缩。
应用FDTD算法对某一个具体的目标进行电磁仿真时,要将目标分解和描述成FDTD仿真软件可以处理的数据格式。在运用FDTD算法早期,由于受计算资源和图形显示设备的局限,用于仿真的建模数据多采用文本编辑形式,对于较复杂物体,很难及时发现建模过程中出现的错误,这种错误将被延续到仿真过程中,而专门的可视化建模模块可以使建模的效率和准确性得到提高。为了使仿真程序具有在不同操作系统的通用性,将电磁学模拟软件分为建模及结果处理模块、仿真模块两个部分,建模及结果处理模块专门进行目标物体的几何和电磁学参数的预设及相关数据的预处理,对模拟结果进行可视化显示;仿真模块专门对建模生成的数据文件进行相应的FDTD电磁模拟。
最后,以具体实例展现该建模模块的可视化效果、友好的图形化界面、结果的精确性和可靠性。
2 建模算法
2.1建模物体的描述
对目标物体进行电磁学建模就是对目标物体的介质参数、几何参数、边界条件、激励源、输出记录等问题的描 述过程,并进行数据的预处理,生成仿真模块处理所需的数据文件。
(1)首先将建模目标物体中使用到的介质参数进行编号并生成介质列表。
(2)然后对目标物体进行几何参数设定,根据FDTD算法和目标物体自身结构特点,在直角坐标系下将物体分解单个矩形块输入。几何参数的输入有两种方式,一种是预先规定各个方向单个网格的尺寸,输入矩形的坐标以网格为单位;另一种是直接输入目标分解的矩形块的实际尺寸。两种情况都要给出矩形区域的介质编号。
(3)对目标物体根据具体问题对计算空间边界选择相应的边界条件,有一阶和二阶Mur、一阶和二阶Dispersive,PMC,PEC,PML等7种边界条件供选择。
(4)目标物体激励源的设定,建模软件激励源采用软激励形式,将激励源信号加在目标物体网格坐标上。在完成上述工作以后,指定用于记录输出的网格坐标,用于记录仿真数据。
2.2 非均匀网格划分算法
为FDTD仿真程序提供尺寸合适的均匀和非均匀网格是建模的重要任务,在物体边界电磁场变化较大的地方宜采用细网格,而在物体边界电磁场变化比较小的地方宜采用粗网格;考虑算法的数值色散的影响,任一网格的尺寸δ≤λmin/12,λmin为关心的上限频率所对应的波长。为了节约计算资源和提高工作效率,对一些较复杂的目标物体采用非均匀网格划分方式。非均匀网格的划分遵守下列规则:
(1)目标物体任一子区域的边界在网格线上。
(2)在各个方向上任意两个相邻网格尺寸比值≤1.25。
进行非均匀网格划分,根据网格密度分布方式有:“密→疏”、“疏→密”、“密→疏→密”等3种分布方式。这里将盼“密→疏→密”非均匀网格为例介绍网格划分算法。
将目标物体在各个方向的几何参数排序划分成若干不重复的子区域,然后在各个子区按上述网格划分规则进行划分。在该模块中,用户可以预先设定3个方向中各个方向最大网格尺寸、最小网格尺寸和相邻网格尺寸比例,然后系统对3个方向网格进行一次性划分,并对网格划分进行规则检测,对用户进行提示,然后用户可以根据各个子区域情况进行优化。这里以X方向上某一子区域上进行网格划分为例来说明。设X方向某个子区域的长度为L,X方向最小的网格尺寸为Xmin,X方向最大网格尺寸Xmax,X方向预设相邻网格比例R∈[1,1.25]。网格的尺寸由区域的一边向中间逐渐增大,然后向另一边逐渐减小。
取该区域长度的一半L/2,令△x=Xmin,由:

式(2)可能得到的不是一个整数,m′取整INT(m′),将m 代入△xRm-1,考虑下面两种情形:
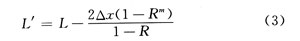
(1)假如△xRm-1≤Xmax令
取K=min{△xRm,Xmax}考虑几种情况:
①若L'≥1.5K,将L'均分为2个网格;
②若1.5K》L'≥K,则L'=K+△L',调整R使△L'=0:
③若L'这样在①条件下生成2m+2个网格,②条件下生成2m+1个网格,③条件下生成2m个网格。
(2)假如△xRm-1》Xmax,找出n1的值,满足,△xRn1-13建模模块及结果处理模块实现
在基于上述非均匀网格划分算法和计算机图形学基础上,我们设计出了可以实现三维复杂物体建模和图形处理的建模可视化模块,可一次性生成仿真软件所需的网格、电磁参数、边界条件和激励源设置等数据文件,可实时实现对数据的监控和修改,实现了对仿真结果的可视化显示。
本文介绍的建模模块可对微带线、微带滤波器、微带电感、贴片天线等无源器件及设备进行建模和分析,实现对目标物体进行二维和三维观察。实现目标物体水平移动、三维转动和放大,并可在网格划分后对划分效果进行二维和三维的观察。图1所示是使用该可视化模块对目标物体建模得到的三维网格图。

4 目标物体建模及模拟结果可视化应用实例
下面将以微带螺旋电感Ⅲ(如图2和图3所示)为例介绍应用该建模模块进行目标物体建模,在模拟以后对模拟结果进行可视化展示。

4.1 目标物体建模
4.1.1 目标物体几何参数及电磁参数输入
首先,根据螺旋电感的实际尺寸确定计算空间的大小,由于网格划分要遍布整个计算空间,为了节约计算资源,保证对螺旋电感的模拟精度,计算空间的范围应大小适中。然后,将螺旋电感分解成若干矩形块,按顺序输入各个矩形块的型值点和材料参数。
4.1.2 网格划分和激励源设置
在输入螺旋电感的几何和材料参数输入完成并检查确定无误的情况下,可以对目标物体在整个计算空间内进行网格划分。然后通过系统检查,对错误的子区域给出标记,建议修改。在完成各子区域内的修改后显示整个计算区域网格的分布。在完成网格划分后,加入激励源。
在完成建模后,调用自行研制的FDTD仿真模块进行运算,输出指定坐标的仿真结果。据此提取的微带螺旋电感特性参数结果一致。
4.2结果可视化
将仿真数据结果处理,在信号处理界面用图表曲线形式来显示出来,螺旋电感输入端口记录电压如图4所示。为直观地表现物理过程,电磁场分布显示界面可以用动画形式显示电磁场随时间步变化演变过程。图5为截取XY面螺旋电感电磁场演变动画中的一幅。

5 结 语
我们研究、设计了用于FDTD仿真软件的电磁建模模块,经过多次建模和模拟实验测试,表明对目标物体建模效率高,生成网格坐标和相关数据准确、高效,建模可视化效果好,对建模目标实现三维多角度实时观察和调整,并且界面友好、操作简单,显著提高了建模的工作效率,进而提高了应用FDTD算法解决具体问题的效率。

 举报
举报






 举报
举报

