PolySwitch元件有多种系列产品,其产品特性各不相同。以常用的RXE系列元件为例,其20℃时的电气特性如表1所示。
表1 RXE系列元件20℃时的电气特性
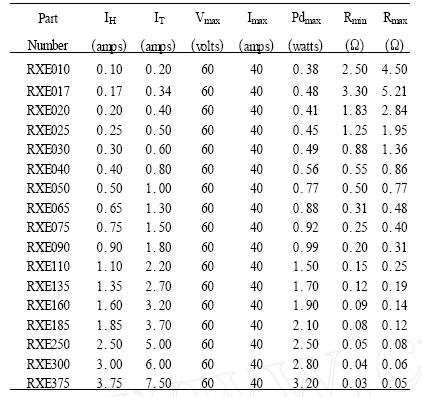
表1中各符号的含义如下:
IH:20℃环境温度下的最大工作电流
IT:20℃环境温度下PolySwitch元件启动保护的最小电流
Vmax:PolySwitch元件的最大工作电压
Imax:PolySwitch元件能承受的最大电流
Pdmax:PolySwitch元件动作状态下的最大消耗功率
Rmax:PolySwitch元件未动作前的初始最大阻值
Rmin:PolySwitch元件未动作前的初始最小阻值
由表1可知,该系列元件所能承受的最大电流为40安培,故障时启动保护的最小电流是最大工作电流的2倍。
RXE系列PolySwitch元件20℃时的动作保护特性曲线见图1。其中横坐标表示故障电流,单位为安培,纵坐标表示动作时间,单位为秒。两个坐标轴均为对数坐标。图中每一条曲线对应一个型号的元件,构成该系列元件的动作保护特性曲线簇。表2为图1中曲线标号与元件型号的对照表。
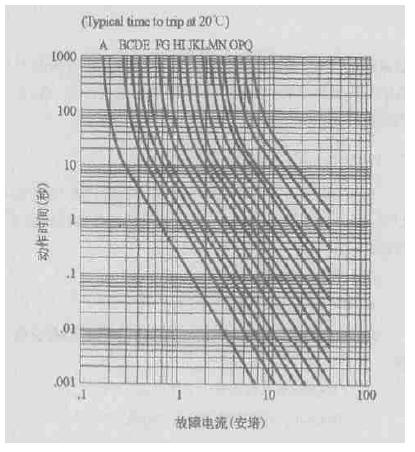
图1 RXE系列元件20℃时的动作保护特性曲线
在图1所示的对数坐标系中,每一条曲线都可看作由弯曲部分和直线部分连接而成,两部分的临界点位置随元件型号的不同而不同。由于各型号元件曲线的变化趋势基本相同,建立数学模型的方法也相同。
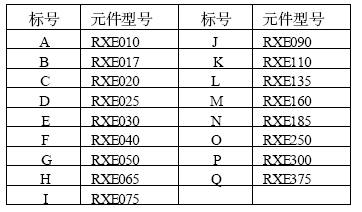
表2 曲线标号与元件型号对照表
数学模型的建立
在图1所示的坐标系中,PolySwitch元件动作保护特性曲线由弯曲部分和直线部分连接而成,可分别建立其数学模型。以M=RXE160的曲线为例,建立数学模型的具体步骤如下。
确定临界点位置
对图1中的曲线进行测量,可得到PolySwitch元件动作保护特性曲线弯曲部分和直线部分的临界点位置。对M=RXE160的曲线,测得的临界点位置约为I=4.3A。
直线部分
由表1可知,RXE系列PolySwitch元件所能承受的最大电流为40A。该点与临界点之间为曲线的直线部分。

由图1直线部分曲线取若干特殊点,经计算机进行数学处理,得到a,b的具体数值:
a=813,b=22.54,
代入(1)式,可得直线部分的数学公式:
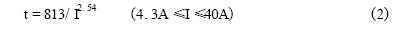
曲线部分
由于PolySwitch元件具有PTC效应,其动作保护特性曲线部分的数学模型可参考PTC器件的阻温特性来建立。该类特性的数学模型可采用幂函数或对数函数的形式。设其数学公式具有如下形式;

式中t0,I0,b均为常数。由图1曲线部分曲线取若干特殊点,经计算机进行数学处理,得到t0,I0,b的具体数值:
t0=-38.93,I0=4.42,b=-1.83,
代入(3)式,可得曲线部分的数学公式:
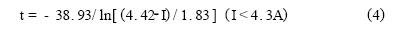
(2)式和(4)式共同组成RXE160元件的动作保护特性数学模型。两条曲线在临界点位置平滑连接。
实验结果
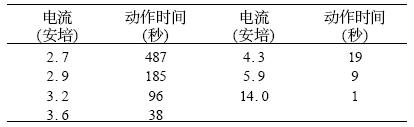
为验证RXE160元件动作保护特性数学模型的正确性,将RXE160元件接入直流电源保护电路中进行实际测试,得到实验数据如表3所示。
表3 实验数据
将实验数据与数学模型曲线绘制在同一坐标系中,如图2所示。图中的曲线为根据(2)式和(4)式绘制的仿真曲线,图中的点为实测数据点。为了方便比较,曲线的横轴、纵轴均采用了对数坐标,所用软件为Matlab6.0。比较图1和图2可知,该仿真曲线与PolySwitch元件手册中给出的动作保护特性曲线形态一致,且与实测数据点之间基本吻合。其他型号曲线的数学模型可按照上述方法分别建立。
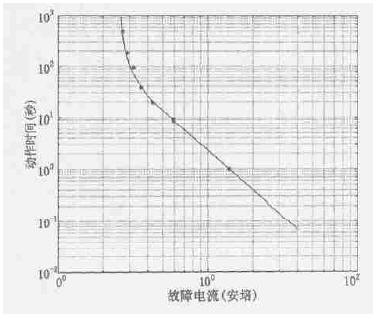
图2 RXE160动作保护特性仿真曲线(20℃)
受元件特性曲线精度的限制,采用查表法选择PolySwitch元件使用不便,而且精度不高。本文根据PolySwitch元件动作保护特性的特点,建立了PolySwitch元件动作保护特性的数学模型,较好地解决了这一问题。实验表明,该仿真曲线与PolySwitch元件手册中给出的动作保护特性曲线形态一致,实测数据与根据数学模型绘制的曲线基本吻合。
PolySwitch元件有多种系列产品,其产品特性各不相同。以常用的RXE系列元件为例,其20℃时的电气特性如表1所示。
表1 RXE系列元件20℃时的电气特性

表1中各符号的含义如下:
IH:20℃环境温度下的最大工作电流
IT:20℃环境温度下PolySwitch元件启动保护的最小电流
Vmax:PolySwitch元件的最大工作电压
Imax:PolySwitch元件能承受的最大电流
Pdmax:PolySwitch元件动作状态下的最大消耗功率
Rmax:PolySwitch元件未动作前的初始最大阻值
Rmin:PolySwitch元件未动作前的初始最小阻值
由表1可知,该系列元件所能承受的最大电流为40安培,故障时启动保护的最小电流是最大工作电流的2倍。
RXE系列PolySwitch元件20℃时的动作保护特性曲线见图1。其中横坐标表示故障电流,单位为安培,纵坐标表示动作时间,单位为秒。两个坐标轴均为对数坐标。图中每一条曲线对应一个型号的元件,构成该系列元件的动作保护特性曲线簇。表2为图1中曲线标号与元件型号的对照表。

图1 RXE系列元件20℃时的动作保护特性曲线
在图1所示的对数坐标系中,每一条曲线都可看作由弯曲部分和直线部分连接而成,两部分的临界点位置随元件型号的不同而不同。由于各型号元件曲线的变化趋势基本相同,建立数学模型的方法也相同。
表2 曲线标号与元件型号对照表

数学模型的建立
在图1所示的坐标系中,PolySwitch元件动作保护特性曲线由弯曲部分和直线部分连接而成,可分别建立其数学模型。以M=RXE160的曲线为例,建立数学模型的具体步骤如下。
确定临界点位置
对图1中的曲线进行测量,可得到PolySwitch元件动作保护特性曲线弯曲部分和直线部分的临界点位置。对M=RXE160的曲线,测得的临界点位置约为I=4.3A。
直线部分
由表1可知,RXE系列PolySwitch元件所能承受的最大电流为40A。该点与临界点之间为曲线的直线部分。

由图1直线部分曲线取若干特殊点,经计算机进行数学处理,得到a,b的具体数值:
a=813,b=22.54,
代入(1)式,可得直线部分的数学公式:
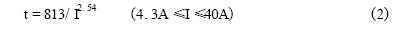
曲线部分
由于PolySwitch元件具有PTC效应,其动作保护特性曲线部分的数学模型可参考PTC器件的阻温特性来建立。该类特性的数学模型可采用幂函数或对数函数的形式。设其数学公式具有如下形式;

式中t0,I0,b均为常数。由图1曲线部分曲线取若干特殊点,经计算机进行数学处理,得到t0,I0,b的具体数值:
t0=-38.93,I0=4.42,b=-1.83,
代入(3)式,可得曲线部分的数学公式:
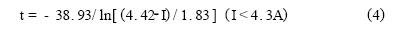
(2)式和(4)式共同组成RXE160元件的动作保护特性数学模型。两条曲线在临界点位置平滑连接。
实验结果
为验证RXE160元件动作保护特性数学模型的正确性,将RXE160元件接入直流电源保护电路中进行实际测试,得到实验数据如表3所示。
表3 实验数据

将实验数据与数学模型曲线绘制在同一坐标系中,如图2所示。图中的曲线为根据(2)式和(4)式绘制的仿真曲线,图中的点为实测数据点。为了方便比较,曲线的横轴、纵轴均采用了对数坐标,所用软件为Matlab6.0。比较图1和图2可知,该仿真曲线与PolySwitch元件手册中给出的动作保护特性曲线形态一致,且与实测数据点之间基本吻合。其他型号曲线的数学模型可按照上述方法分别建立。

图2 RXE160动作保护特性仿真曲线(20℃)
受元件特性曲线精度的限制,采用查表法选择PolySwitch元件使用不便,而且精度不高。本文根据PolySwitch元件动作保护特性的特点,建立了PolySwitch元件动作保护特性的数学模型,较好地解决了这一问题。实验表明,该仿真曲线与PolySwitch元件手册中给出的动作保护特性曲线形态一致,实测数据与根据数学模型绘制的曲线基本吻合。

 举报
举报







 举报
举报

