建立时间是运放阶跃响应进入和停留在最终值的特定误差范围内的所需时间。它在一些应用中十分重要,例如驱动AD转换器,数字化的快速变化输入。但我们先超越这个定义看一看,聚焦在建立波形的特性上。
之前关于压摆率的博文中讲到一个运放是如何从陡升斜坡到小信号稳定波形上的转变,如Figure1。随着增益的上升,你可以看到靠近最终值的速度也变慢了。这是因为增益更高,闭环带宽减小。
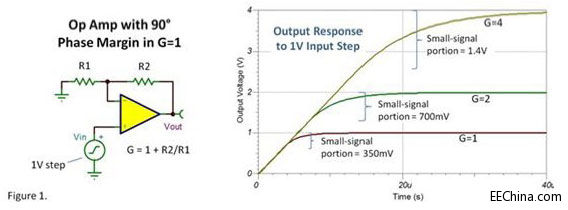
此例子的运放在增益为1的时候相位裕量约为90°。请注意即使是单位增益时也没有过冲。它近乎完美的一阶响应就像一个标准品,可以作为比较的基准,但你不太可能找到一个运放在增益为1的情况下拥有如此充足的相位裕量。
Figure 2中的响应更符合实际(也许有点悲观)。这些波形来自同一个运放,这个运放在增益为1时的相位裕量约35°(理想运放的响应也列出以供对比)。G=1时它的小信号过冲约为32%,它的1V阶跃响应显得比较小,因为只有小信号部分的响应才会产生过冲。更大的输入阶跃信号会有相同的幅值的过冲,但看起来比例上比较小。这就是为什么你一直要用小阶跃信号来检查过冲和稳定性。
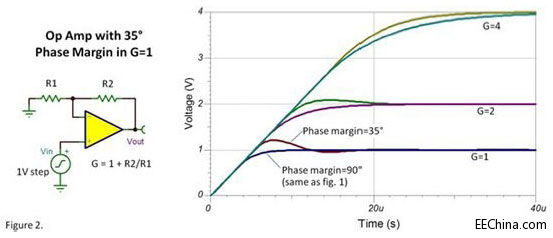
图 3 为G=1情况下的小信号阶跃响应。可以看到,信号达到稳态的过程需要两个波动周期。波动还在继续,但越来越小——直到超出图片的分辨能力。因此,通常还需要一个或两个的额外的周期来让信号稳定到高精度。
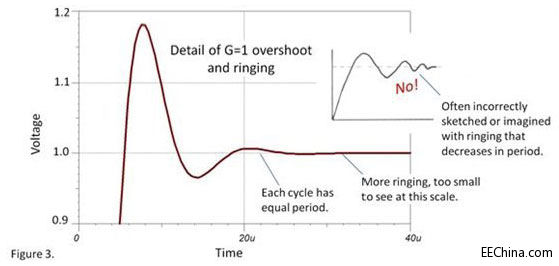
模拟系统到达稳定的过程中,我们经常倾向于认为最后的过冲周期越来越小,好像振铃的自身频率在一个个波峰中越来越快。
真正稳定到高精度,16-bit或更高所需的时间常常还包括其他因素。发烧友做的相位补偿技术以及热效应的影响都要考虑在内。ADC输入端的开关信号带来的影响也是放大器电路需要当心的问题。优化所有的这些问题会是个棘手的事情。当然,仿真运放工作时,压摆率在二阶系统中的影响也很重要。
建立时间是运放阶跃响应进入和停留在最终值的特定误差范围内的所需时间。它在一些应用中十分重要,例如驱动AD转换器,数字化的快速变化输入。但我们先超越这个定义看一看,聚焦在建立波形的特性上。
之前关于压摆率的博文中讲到一个运放是如何从陡升斜坡到小信号稳定波形上的转变,如Figure1。随着增益的上升,你可以看到靠近最终值的速度也变慢了。这是因为增益更高,闭环带宽减小。

此例子的运放在增益为1的时候相位裕量约为90°。请注意即使是单位增益时也没有过冲。它近乎完美的一阶响应就像一个标准品,可以作为比较的基准,但你不太可能找到一个运放在增益为1的情况下拥有如此充足的相位裕量。
Figure 2中的响应更符合实际(也许有点悲观)。这些波形来自同一个运放,这个运放在增益为1时的相位裕量约35°(理想运放的响应也列出以供对比)。G=1时它的小信号过冲约为32%,它的1V阶跃响应显得比较小,因为只有小信号部分的响应才会产生过冲。更大的输入阶跃信号会有相同的幅值的过冲,但看起来比例上比较小。这就是为什么你一直要用小阶跃信号来检查过冲和稳定性。

图 3 为G=1情况下的小信号阶跃响应。可以看到,信号达到稳态的过程需要两个波动周期。波动还在继续,但越来越小——直到超出图片的分辨能力。因此,通常还需要一个或两个的额外的周期来让信号稳定到高精度。

模拟系统到达稳定的过程中,我们经常倾向于认为最后的过冲周期越来越小,好像振铃的自身频率在一个个波峰中越来越快。
真正稳定到高精度,16-bit或更高所需的时间常常还包括其他因素。发烧友做的相位补偿技术以及热效应的影响都要考虑在内。ADC输入端的开关信号带来的影响也是放大器电路需要当心的问题。优化所有的这些问题会是个棘手的事情。当然,仿真运放工作时,压摆率在二阶系统中的影响也很重要。

 举报
举报





 举报
举报

