电子干扰是现代电子战的重要组成部分,包括无源干扰和有源干扰,其中,有源干扰可以分为欺骗干扰和遮蔽干扰。欺骗干扰是采用假的目标和信息作用于雷达的目标检测和跟踪系统,使雷达不能正确的检测真实目标或者不能正确的测量真正目标的参数信息,从而达到迷惑或扰乱雷达对真正目标检测和跟踪的目的。遮盖式的干扰是使用噪声或类似噪声的干扰信号遮盖或淹没有用信号,阻止雷达检测目标信息。对于欺骗干扰可以使用与雷达信号的识别方法对其进行检测设别,但是对于使用噪声调制的遮蔽干扰信号,因为其自身的强随机性,很难使用雷达信号的检测识别方法。但是由于干扰信号是时间上连续的信号,在一定的时间内采样的数目可以很大;而对雷达来说,积累个数受到目标照射时间和脉冲间隔的限制,这是干扰噪声检测的优势所在,也成为了寻求检测遮蔽干扰信号的突破口。
1 噪声调频信号功率谱检测原理
噪声调频干扰信号最常见的是射频振荡的频率与调制噪声电压ξ(t)成线性关系,为了方便把噪声调频,信号的时域如式(1)
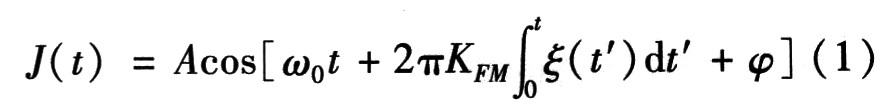
设调制噪声电压ξ(t)是高斯噪声,其幅度概率密度分布为高斯函数
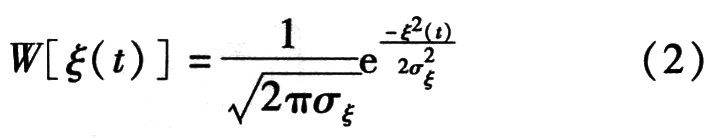
由于噪声调频干扰的角频率与ξ(t)呈线性关系,故瞬时角频率或角频偏的概率密度也应为高斯分布,其均方根的值为

式(6)中的积分只有在mfe》1和mfe《1时才能近似求解。
当mfe》1可以得到噪声调频信号的干扰带宽(半功率带宽)为
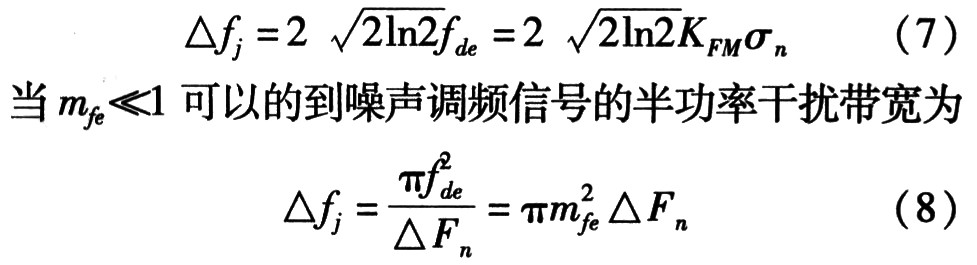
对于噪声调频信号,由于信号的随机性很强,很难在使用相关的办法对这类噪声调制的信号进行检测,所以常用的瞬时相关、时频分布等检测方法对其无效。但是由于接收系统在设计时,其系统的热噪声相对比较稳定,所以其热噪声功率谱也是相对稳定的。当由调频干扰信号进入接收机时,根据式(6),其功率谱在干扰频带[f0一△fj/2,f0+△fj/2]内会比无调频干扰信号时在能量上有明显的提高,根据这一特征,可以检测出干扰信号。并相应的确定带宽和中心频率,如图l所示。
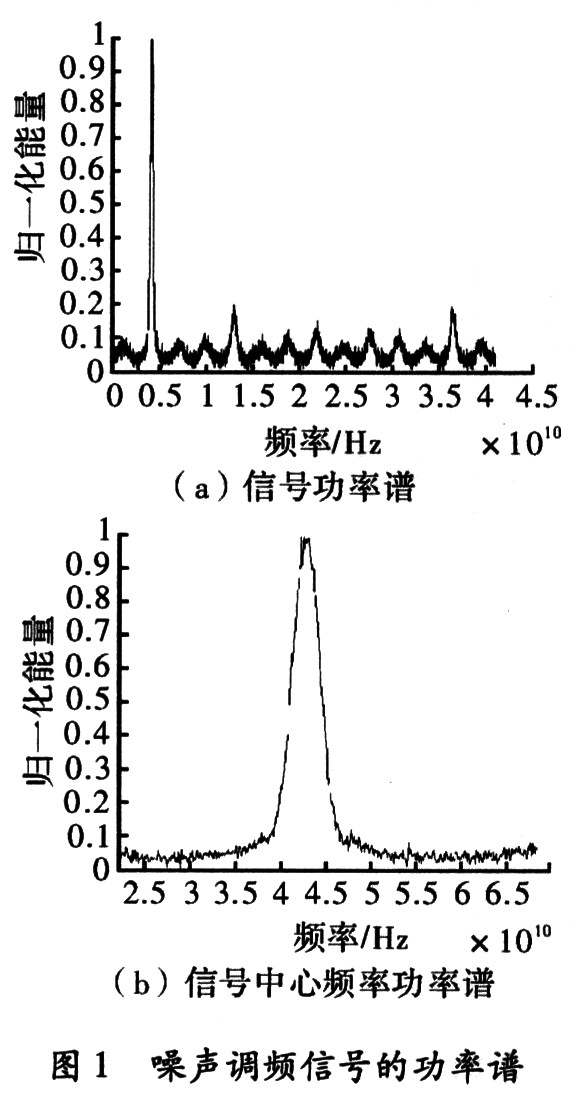
图1中噪声调频信号的中心频率4.3 GHz,每伏调制为1 GHz/V,时长10 ms,为了提高检测带宽按单次时长100 ns做4 096采样,循环10 000次累积处理。在实用的条件下一般会至少做到几十毫秒的时长来进行累计。产生的白噪声调制信号首先经过256阶的带通滤波器,用来给生成的白噪声滤波进行色化处理,通带为4.29~4.31 GHz,所以视频调频带宽20 MHz。经过滤波后的随机数带入到式(1),得到噪声调频信号,然后计算功率谱,结果如图1(a)所示。从图1(a)中可以看到在40 GHz的检测带宽中,信号的能量主要集中在4.3 GHz左右。图1(b)为中心频率处放大图形,可以看出干扰信号的3 dB带宽(即归一化能量的0.707左右处)为0.18 GHz,10 dB带宽(归一化能量0.3左右处)为0.37 GHz。
当白噪声累加到调频干扰后在得到的功率谱,如图2所示。
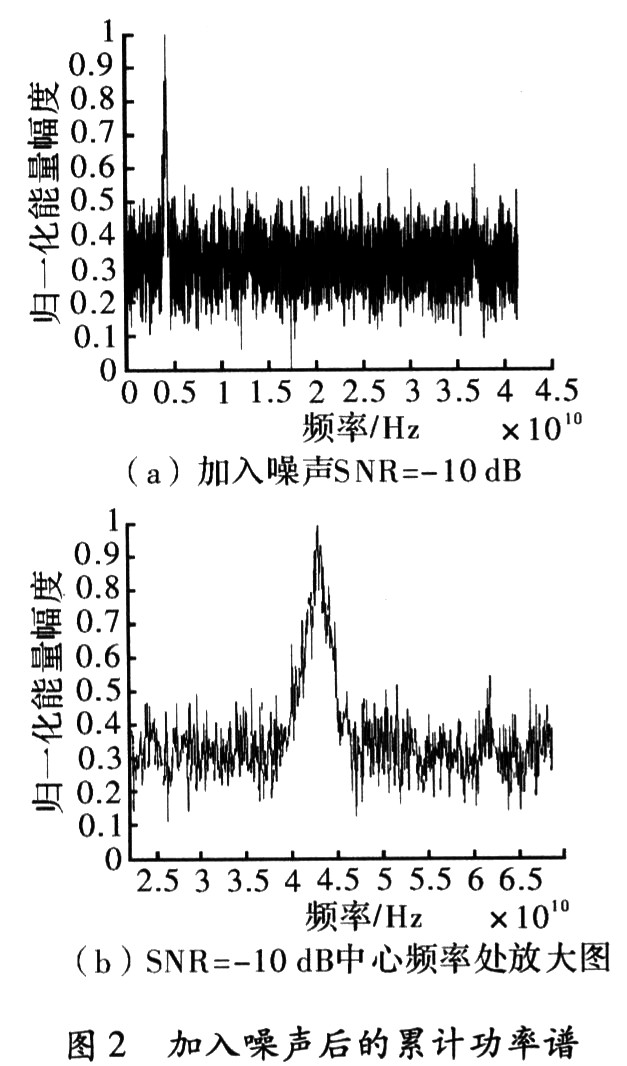
从图2中可以看出在SNR=一10 dB情况下,可以检测处噪声调频干扰信号,且在中心频率处的能量有所衰减。由于考虑仿真速度的需要此处所取时长较短,如果加长时间的积累,即相当于增加了能量的积累,得到的检测灵敏度会更高。对于检测门限的设定,是在实际应用中关心的问题。这里简述两种参考门限的确定方法。第一,对于系统的热噪声是在设计时所确定的固有性质,相对外界环境要稳定的多,在设置门限时可以考虑当切断外来所有的信号输入,得到的机内热噪声的功率均值数作为参考门限,这样的好处是确保此时噪声纯净,缺点是没有考虑环境噪声的存在,从而出现虚警的概率增加,这也是文中使用的方法;第二,是在侦察天线没有对准干扰源的情况下,得到内外混合噪声的各个频点的功率均值作为参考门限,其优点是能够真实的反映实际情况,但是如果此时有其它发射机信号的输入,则检测出现漏警的概率会大大增加。
2 相似理论
在信号与系统学科中,相关性是一种在时域中对信号特性进行描述的重要方法。由于信号与其功率谱函数是一对傅里叶变换,在信号分析中往往利用它来分析随机信号的功率谱分布,以致不少人一提到相关性马上会联想到信号功率谱的计算。假设得到的两信号分别为X(t),Y(t)。可以选择当倍数K使KY(t)去逼近X(t)。在此可以借用误差能量来度量波形的相似程度。
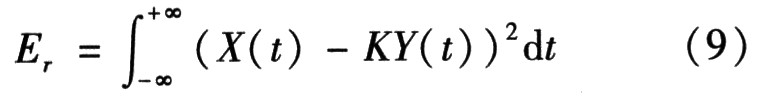
其中Er代表误差能量,K的选择是为了使误差能量最小,可以得出
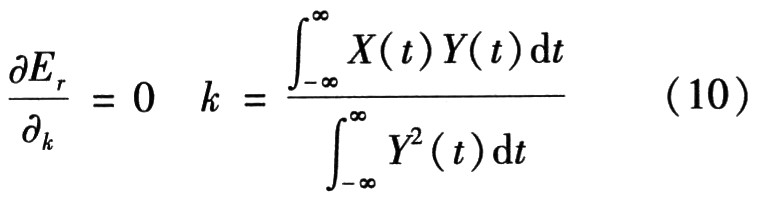
另外,可定义相对误差能量为
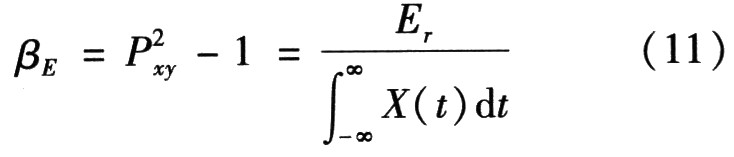
其中Pxy为相关系数。可以推出
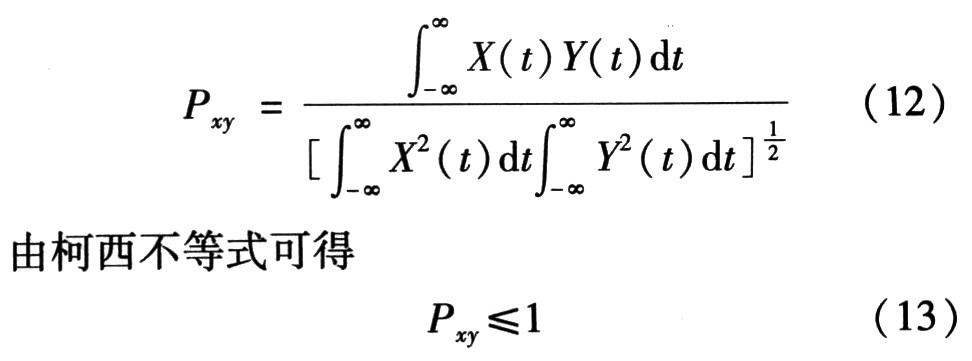
对于能量有限的信号而言,能量是确定的,相关系数的大小只由X(t)*Y(t)积分决定。若两个完全不相似的信号,其幅度取值和出现时刻是相互独立、彼此无关的,即X(t)*Y(t)=0,其积分结果也为0,所以当相关系数为O时相似度最差,即不相关。当相关系数为1时,则误差能量为0,说明这两个信号相似度很好,是线性相关的。因此把相关系数作为两个信号相似性的度量完全是有理论依据的、合理的。
3 利用相似理论的噪声调频信号检测
为了讨论方便,假设接收机为理想接收机,即在通带内,其幅频特性为一固定值,相频为线性,而通带之外增益为零,中心频率ω0为且远大于接收机带宽△ω,并假定背景噪声是高斯白噪声,这种假设不失一般性,基本可以很好地描述常规接收机的检测特性。
在时长1 ms,信噪比从一10~10 dB进行100次蒙特卡洛实验,其信号具体形式如第2节所述,首先得到信号和基准白噪声的各自的功率谱,然后代入式(12)中,计算其相关系数。考虑到虚警的可能性,通常认为当相关系数<0.8时存在噪声调频干扰,否则没有噪声干扰信号进入。所得结果,如图3所示。
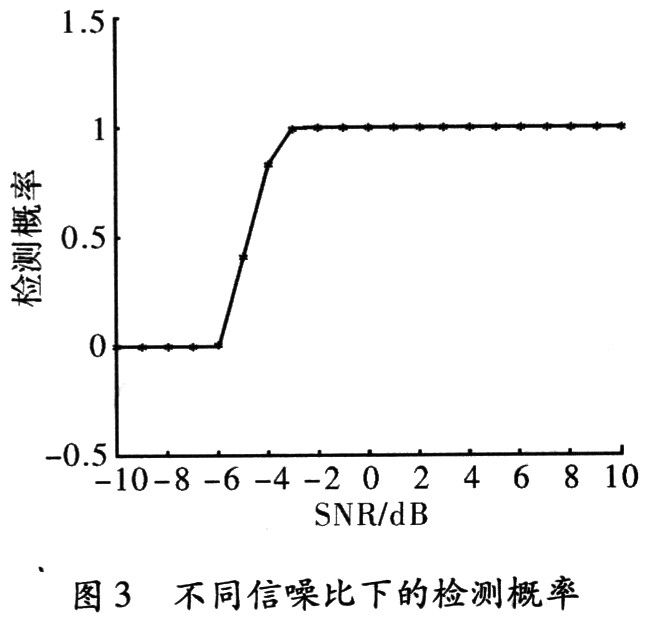
从图3可以看出在信噪比一3 dB以上能够在时长0.1 ms下做到100%的检测。充分说明了该方法对检测识别噪声调频信号是可行的。而且根据积累时长的不同,对算法检测的灵敏度影响很大,在图4给出了不同积累时间10次蒙特卡洛实验的检测概率。
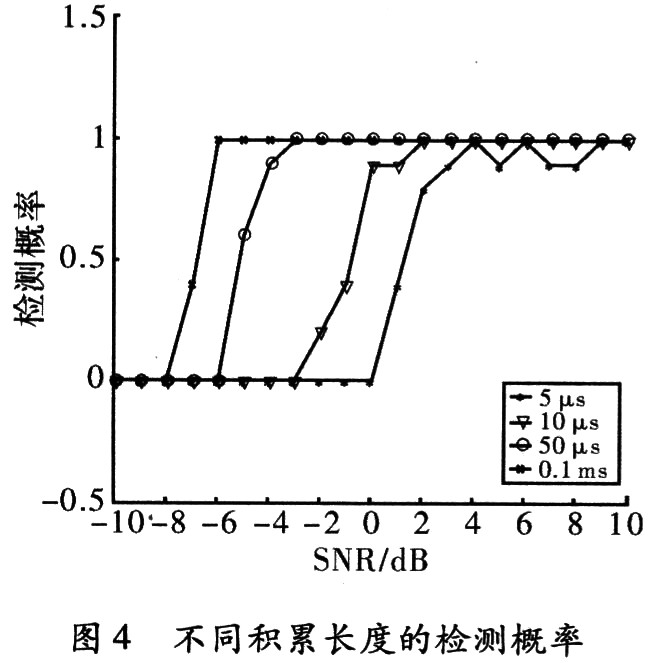
从图4中可以看出,随着时长的增加不但检测灵敏度有比较明显的提高,同时检测曲线更加的平滑,误差减小。
4 结束语
由于噪声调频信号的强随机性,利用相关的各种检测方法无法对此类信号做出有效的检测。文中利用功率谱积累和相似函数的方法对噪声调频信号进行了检测,通过仿真试验验证了方法的可行性,说明检测概率与信噪比和累计时间长度的关系。
电子干扰是现代电子战的重要组成部分,包括无源干扰和有源干扰,其中,有源干扰可以分为欺骗干扰和遮蔽干扰。欺骗干扰是采用假的目标和信息作用于雷达的目标检测和跟踪系统,使雷达不能正确的检测真实目标或者不能正确的测量真正目标的参数信息,从而达到迷惑或扰乱雷达对真正目标检测和跟踪的目的。遮盖式的干扰是使用噪声或类似噪声的干扰信号遮盖或淹没有用信号,阻止雷达检测目标信息。对于欺骗干扰可以使用与雷达信号的识别方法对其进行检测设别,但是对于使用噪声调制的遮蔽干扰信号,因为其自身的强随机性,很难使用雷达信号的检测识别方法。但是由于干扰信号是时间上连续的信号,在一定的时间内采样的数目可以很大;而对雷达来说,积累个数受到目标照射时间和脉冲间隔的限制,这是干扰噪声检测的优势所在,也成为了寻求检测遮蔽干扰信号的突破口。
1 噪声调频信号功率谱检测原理
噪声调频干扰信号最常见的是射频振荡的频率与调制噪声电压ξ(t)成线性关系,为了方便把噪声调频,信号的时域如式(1)
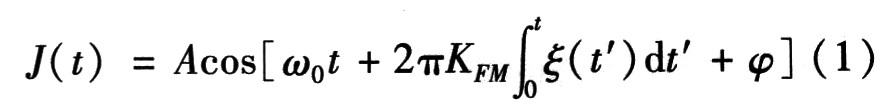
设调制噪声电压ξ(t)是高斯噪声,其幅度概率密度分布为高斯函数
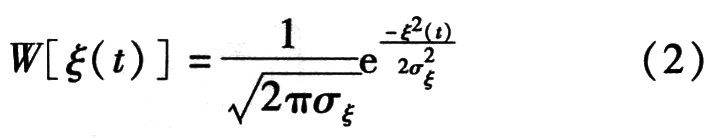
由于噪声调频干扰的角频率与ξ(t)呈线性关系,故瞬时角频率或角频偏的概率密度也应为高斯分布,其均方根的值为

式(6)中的积分只有在mfe》1和mfe《1时才能近似求解。
当mfe》1可以得到噪声调频信号的干扰带宽(半功率带宽)为
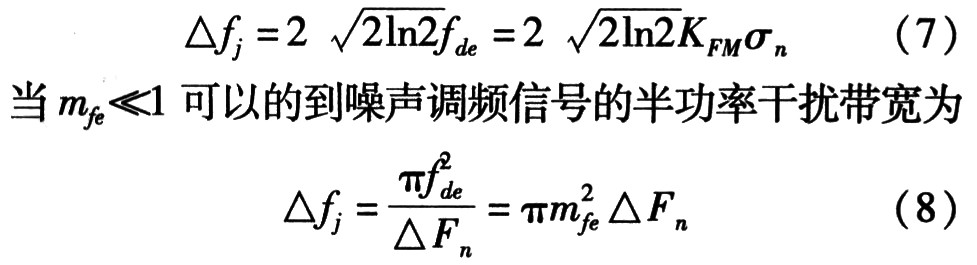
对于噪声调频信号,由于信号的随机性很强,很难在使用相关的办法对这类噪声调制的信号进行检测,所以常用的瞬时相关、时频分布等检测方法对其无效。但是由于接收系统在设计时,其系统的热噪声相对比较稳定,所以其热噪声功率谱也是相对稳定的。当由调频干扰信号进入接收机时,根据式(6),其功率谱在干扰频带[f0一△fj/2,f0+△fj/2]内会比无调频干扰信号时在能量上有明显的提高,根据这一特征,可以检测出干扰信号。并相应的确定带宽和中心频率,如图l所示。

图1中噪声调频信号的中心频率4.3 GHz,每伏调制为1 GHz/V,时长10 ms,为了提高检测带宽按单次时长100 ns做4 096采样,循环10 000次累积处理。在实用的条件下一般会至少做到几十毫秒的时长来进行累计。产生的白噪声调制信号首先经过256阶的带通滤波器,用来给生成的白噪声滤波进行色化处理,通带为4.29~4.31 GHz,所以视频调频带宽20 MHz。经过滤波后的随机数带入到式(1),得到噪声调频信号,然后计算功率谱,结果如图1(a)所示。从图1(a)中可以看到在40 GHz的检测带宽中,信号的能量主要集中在4.3 GHz左右。图1(b)为中心频率处放大图形,可以看出干扰信号的3 dB带宽(即归一化能量的0.707左右处)为0.18 GHz,10 dB带宽(归一化能量0.3左右处)为0.37 GHz。
当白噪声累加到调频干扰后在得到的功率谱,如图2所示。

从图2中可以看出在SNR=一10 dB情况下,可以检测处噪声调频干扰信号,且在中心频率处的能量有所衰减。由于考虑仿真速度的需要此处所取时长较短,如果加长时间的积累,即相当于增加了能量的积累,得到的检测灵敏度会更高。对于检测门限的设定,是在实际应用中关心的问题。这里简述两种参考门限的确定方法。第一,对于系统的热噪声是在设计时所确定的固有性质,相对外界环境要稳定的多,在设置门限时可以考虑当切断外来所有的信号输入,得到的机内热噪声的功率均值数作为参考门限,这样的好处是确保此时噪声纯净,缺点是没有考虑环境噪声的存在,从而出现虚警的概率增加,这也是文中使用的方法;第二,是在侦察天线没有对准干扰源的情况下,得到内外混合噪声的各个频点的功率均值作为参考门限,其优点是能够真实的反映实际情况,但是如果此时有其它发射机信号的输入,则检测出现漏警的概率会大大增加。
2 相似理论
在信号与系统学科中,相关性是一种在时域中对信号特性进行描述的重要方法。由于信号与其功率谱函数是一对傅里叶变换,在信号分析中往往利用它来分析随机信号的功率谱分布,以致不少人一提到相关性马上会联想到信号功率谱的计算。假设得到的两信号分别为X(t),Y(t)。可以选择当倍数K使KY(t)去逼近X(t)。在此可以借用误差能量来度量波形的相似程度。
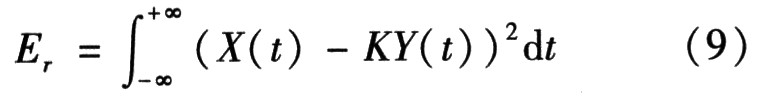
其中Er代表误差能量,K的选择是为了使误差能量最小,可以得出
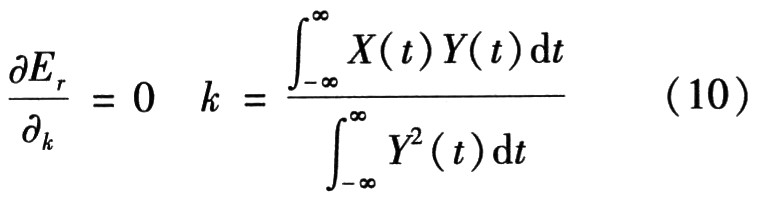
另外,可定义相对误差能量为
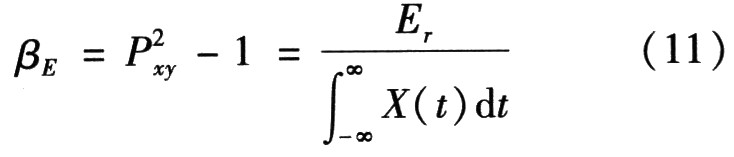
其中Pxy为相关系数。可以推出
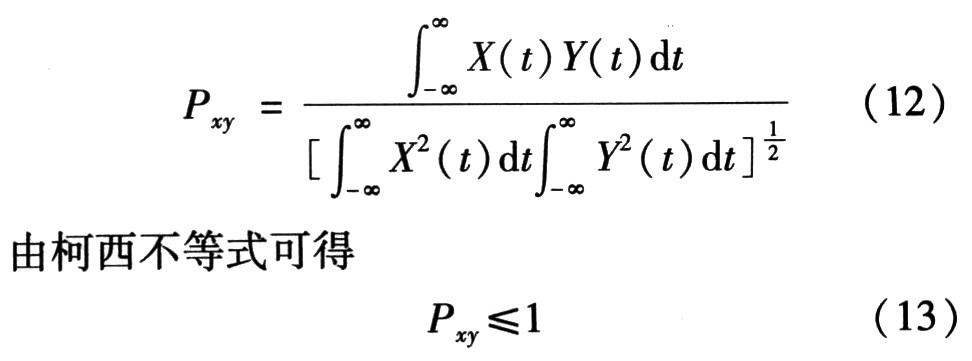
对于能量有限的信号而言,能量是确定的,相关系数的大小只由X(t)*Y(t)积分决定。若两个完全不相似的信号,其幅度取值和出现时刻是相互独立、彼此无关的,即X(t)*Y(t)=0,其积分结果也为0,所以当相关系数为O时相似度最差,即不相关。当相关系数为1时,则误差能量为0,说明这两个信号相似度很好,是线性相关的。因此把相关系数作为两个信号相似性的度量完全是有理论依据的、合理的。
3 利用相似理论的噪声调频信号检测
为了讨论方便,假设接收机为理想接收机,即在通带内,其幅频特性为一固定值,相频为线性,而通带之外增益为零,中心频率ω0为且远大于接收机带宽△ω,并假定背景噪声是高斯白噪声,这种假设不失一般性,基本可以很好地描述常规接收机的检测特性。
在时长1 ms,信噪比从一10~10 dB进行100次蒙特卡洛实验,其信号具体形式如第2节所述,首先得到信号和基准白噪声的各自的功率谱,然后代入式(12)中,计算其相关系数。考虑到虚警的可能性,通常认为当相关系数<0.8时存在噪声调频干扰,否则没有噪声干扰信号进入。所得结果,如图3所示。

从图3可以看出在信噪比一3 dB以上能够在时长0.1 ms下做到100%的检测。充分说明了该方法对检测识别噪声调频信号是可行的。而且根据积累时长的不同,对算法检测的灵敏度影响很大,在图4给出了不同积累时间10次蒙特卡洛实验的检测概率。

从图4中可以看出,随着时长的增加不但检测灵敏度有比较明显的提高,同时检测曲线更加的平滑,误差减小。
4 结束语
由于噪声调频信号的强随机性,利用相关的各种检测方法无法对此类信号做出有效的检测。文中利用功率谱积累和相似函数的方法对噪声调频信号进行了检测,通过仿真试验验证了方法的可行性,说明检测概率与信噪比和累计时间长度的关系。

 举报
举报


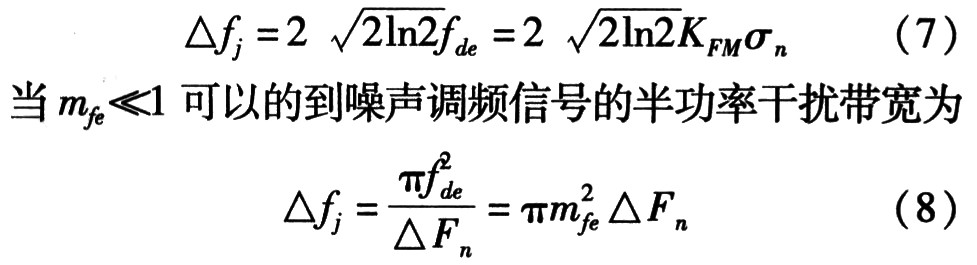


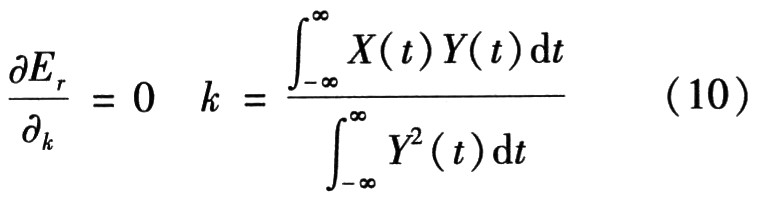
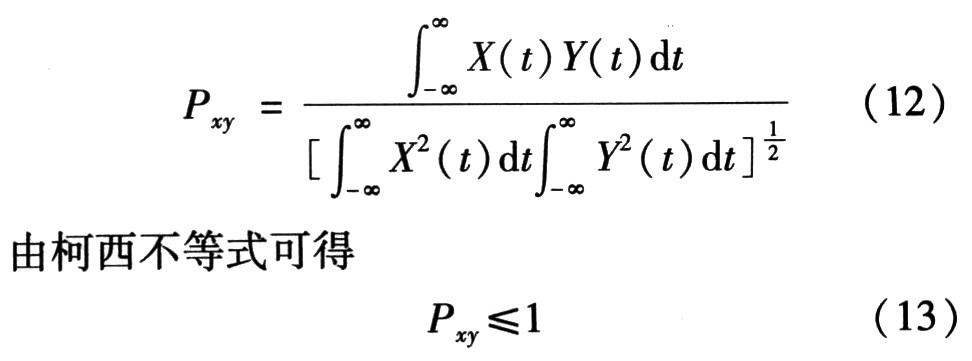



 举报
举报

