随着大规模集成电路技术和微型计算机技术的飞速发展,计算机化已经成为遥测技术发展的方向和特征。传统的模拟式频分多路遥测系统已越来越无法适应现代遥测技术的发展。因为它具有以下致命的缺点:(1)解调输出的模拟信号无法直接供计算机处理和分析;(2)系统参数一旦设定,就无法改变,系统灵活性差。为了克服以上缺点,有必要对模拟式频分多路遥测系统进行根本性的变革,研制新型的数字式频分多路副载波解调器。
幸运的是,数字信号处理技术和大规模集成电路技术的迅猛发展,为我们设计数字式频分多路副载波解调器提供了新思路和新方法。近几年来,现场可编程门阵列(FPGA)因其具有集成度高、处理速度快以及执行效率高等优点?1,在数字系统的设计中得到了广泛应用。本文所提及的数字式频分多路副载波解调器就是利用FPGA技术来实现的。
1 总体设计方案
设计的数字式频分多路遥测系统副载波解调器是IRIG-CBW-E标准的,即通道中心频率分别为128、256、384、512、640和768kHz,频偏为32kHz,调制信号频率范围为100Hz~25kHz。
1.1 系统组成
该数字式频分多路副载波解调器应用了数字信号处理技术和频谱搬移的思想,先将模拟调频信号数字化,再对其进行数字式解调。解调后输出的是数字信号,可以直接供数字化设备进行存储和分析。另外,也可将该数字信号进行模拟重建,恢复出原始模拟信号。其组成框图如图1所示。
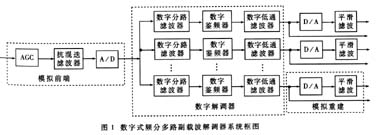
由图1可见,数字式频分多路副载波解调器主要由模拟前端、数字解调器和模拟重建部分等三部分构成。其中,模拟前端包括AGC电路、抗混迭滤波器及A/D变换器。
模拟前端作为模拟部分和数字部分的接口电路,主要完成多路调频信号的预处理和A/D变换。模拟重建部分包括D/A变换器和平滑滤波器。它将解调后的数字信号转换成模拟信号。并放大到所需电平。
数字解调器是系统的核心。它由数字式分路滤波器、数字式鉴频器以及数字式低通滤波器三部分构成。它将完成多路调频信号的分路滤波和解调任务。图2给出了单路数字式解调器的数学模型。
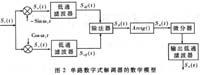
由图2可以看出,我们并没有采用数字式锁相环,而是采用数字信号处理(DSP)算法来实现解调。这种方案更适合用FPGA来实现。
1.2 硬件电路设计
为了便于调试,在进行硬件电路设计时,将数字解调器、A/D及D/A三部分分别放在不同的电路板上,通过双排插头进行连接。A/D变换器是依据数字解调器的采样频率和数据宽度进行选择的。因数字解调器的采样频率为2.56kHz,数据位宽为8位,故选择了易于调试的8位高速模/数转换器TLC5510。D/A变换器选用了Maxim公司的MX7545。而数字解调器选用了Altera公司的FLEX10K系列器件。利用MAX+ plusII进行硬件仿真时,单路数字解调器共需三块FLEX10K50,且其利用率可达75%以上。若重复采用相同的方法进行多路信号的解调,必然会使硬件资源成倍增加。显然,这是不经济和不可行的。因此,如何在不增加或少增加系统硬件规模的前提下,完成对多路信号的解调,则成为设计过程中要着重解决的关键问题。
2 关键技术
为了在尽可能节省系统资源的前提下,完成多路信号的解调任务,采用了时分复用的方法。利用FPGA实现数字式解调器,具备了时分复用的条件。
一方面,采用的FPGA其处理数据的速度可达100MSPS,而本系统采样率为2.56MHz,即要求处理速度为2.56MSPS,所以从理论上说,利用它同时处理30路以上的信号是有可能的。考虑到实际系统不可能工作在最大处理速度下,假定只能达到最大速度的1/3,则采用时分复用后,至少也能同时处理10路以上的信号。
另一方面,由于每一路分路滤波器(包括同相支路和正交支路)都采用64阶FIR低通滤波器,其带宽、过渡带带宽和阻带衰减完全相同,也就是说冲激响应完全相同,所以构成FIR滤波器的矢量乘法器可以重复利用。每一路输出低通滤波器也都具有相同的电路结构。在原理上,它与分路滤波器完全相同,因此这里只以分路滤波器为例进行讨论。FIR滤波器主要由移位寄存器、相加器及矢量乘法器构成?2,其中矢量乘法器在FIR滤波器中占用了大部分硬件资源。因此,节省矢量乘法器,便可以节省系统资源。由此可见,时分复用的实质是指矢量乘法器的时分复用。
下面以实例说明时分复用的实现方法。
为讨论方便,假定FIR滤波器的阶数为8阶,时分复用的路数k=2。设FIR滤波器的冲激响应为h?n ,第一路输入信号为x1?n ,第二路输入信号为x2?n ,滤波器的工作频率为2倍输入数据率。两路信号经复合器形成组合信号,其时序如图3所示。
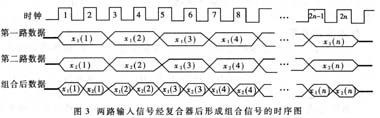
由图3可以看出,复合器输出的组合信号实际上是将第一路信号和第二路信号进行了交织,在奇数时刻出现的为第一路信号,在偶数时刻出现的为第二路信号。为使同一路信号同时从移位相加器中输出到矢量乘法器,必须保证在奇数时刻移位相加器输出的信号都为第一路信号,而偶数时刻输出的信号都为第二路信号。此外还要保证两路数据都能够在时钟的控制下顺序移位。为了满足上述条件,设计了两路信号复用的FIR滤波器,其结构框图如图4所示。
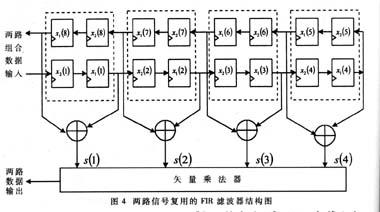
该滤波器只是在8阶FIR滤波器的基础上增加了8个移位寄存器?3,正是这8个移位寄存器使得矢量乘法器计算第一路信号时,第二路信号得以缓存;而在下一时刻到来时,才将第二路信号输出给矢量乘法器。这样就完成了两路信号的同时滤波。滤波后的信号仍以交织的形式输出,可利用分路器将它们分开。
同理,如果同时进行k路滤波,则滤波器中移位寄存器的个数将是单路FIR滤波器中移位寄存器个数的k倍。即假定FIR滤波器的阶数为N,则单路滤波器需要移位寄存器的个数为N,k路滤波器需要的移位寄存器个数为k·N。 另外,值得注意的是:采用时分复用方法后,整个系统就工作于不同的时钟频率下。假定系统采样频率为fs,进行时分复用后同时处理k路信号,则非时分复用部分的时钟频率为fs,时分复用部分的时钟频率为k·fs为使系统能够正常工作,还要在系统中加上时钟和控制电路,以控制系统的时钟和同步。图5给出了分路滤波器的时分复用框图。

利用MAX+plusII对两路信号复用滤波器的AHDL源代码进行编译,发现两路信号复用滤波器比单路滤波器多用的硬件资源不到单路硬件资源的20%。所以说,利用时分复用的方法达到了预期目标。
这种基于FPGA的数字式解调器的优点是容易和计算机相结合形成数字式FM-FM遥测数据处理系统。一方面,遥测数据可以传送给计算机,进行存储、分析和显示;另一方面,计算机也可以给数字式解调器加载不同的程序,以改变解调器的参数设置,使之适合于IRIG的全部标准。
但是,该数字式解调器仍有其不足之处,即运算精度不够高,因为利用FPGA难以进行浮点运算。如果滤波器用FPGA实现,数据宽度取12bit,鉴频器用DSP实现,采用浮点运算,则系统精度必会得到改善,但付出的代价是系统复杂度增加。
随着大规模集成电路技术和微型计算机技术的飞速发展,计算机化已经成为遥测技术发展的方向和特征。传统的模拟式频分多路遥测系统已越来越无法适应现代遥测技术的发展。因为它具有以下致命的缺点:(1)解调输出的模拟信号无法直接供计算机处理和分析;(2)系统参数一旦设定,就无法改变,系统灵活性差。为了克服以上缺点,有必要对模拟式频分多路遥测系统进行根本性的变革,研制新型的数字式频分多路副载波解调器。
幸运的是,数字信号处理技术和大规模集成电路技术的迅猛发展,为我们设计数字式频分多路副载波解调器提供了新思路和新方法。近几年来,现场可编程门阵列(FPGA)因其具有集成度高、处理速度快以及执行效率高等优点?1,在数字系统的设计中得到了广泛应用。本文所提及的数字式频分多路副载波解调器就是利用FPGA技术来实现的。
1 总体设计方案
设计的数字式频分多路遥测系统副载波解调器是IRIG-CBW-E标准的,即通道中心频率分别为128、256、384、512、640和768kHz,频偏为32kHz,调制信号频率范围为100Hz~25kHz。
1.1 系统组成
该数字式频分多路副载波解调器应用了数字信号处理技术和频谱搬移的思想,先将模拟调频信号数字化,再对其进行数字式解调。解调后输出的是数字信号,可以直接供数字化设备进行存储和分析。另外,也可将该数字信号进行模拟重建,恢复出原始模拟信号。其组成框图如图1所示。

由图1可见,数字式频分多路副载波解调器主要由模拟前端、数字解调器和模拟重建部分等三部分构成。其中,模拟前端包括AGC电路、抗混迭滤波器及A/D变换器。
模拟前端作为模拟部分和数字部分的接口电路,主要完成多路调频信号的预处理和A/D变换。模拟重建部分包括D/A变换器和平滑滤波器。它将解调后的数字信号转换成模拟信号。并放大到所需电平。
数字解调器是系统的核心。它由数字式分路滤波器、数字式鉴频器以及数字式低通滤波器三部分构成。它将完成多路调频信号的分路滤波和解调任务。图2给出了单路数字式解调器的数学模型。

由图2可以看出,我们并没有采用数字式锁相环,而是采用数字信号处理(DSP)算法来实现解调。这种方案更适合用FPGA来实现。
1.2 硬件电路设计
为了便于调试,在进行硬件电路设计时,将数字解调器、A/D及D/A三部分分别放在不同的电路板上,通过双排插头进行连接。A/D变换器是依据数字解调器的采样频率和数据宽度进行选择的。因数字解调器的采样频率为2.56kHz,数据位宽为8位,故选择了易于调试的8位高速模/数转换器TLC5510。D/A变换器选用了Maxim公司的MX7545。而数字解调器选用了Altera公司的FLEX10K系列器件。利用MAX+ plusII进行硬件仿真时,单路数字解调器共需三块FLEX10K50,且其利用率可达75%以上。若重复采用相同的方法进行多路信号的解调,必然会使硬件资源成倍增加。显然,这是不经济和不可行的。因此,如何在不增加或少增加系统硬件规模的前提下,完成对多路信号的解调,则成为设计过程中要着重解决的关键问题。
2 关键技术
为了在尽可能节省系统资源的前提下,完成多路信号的解调任务,采用了时分复用的方法。利用FPGA实现数字式解调器,具备了时分复用的条件。
一方面,采用的FPGA其处理数据的速度可达100MSPS,而本系统采样率为2.56MHz,即要求处理速度为2.56MSPS,所以从理论上说,利用它同时处理30路以上的信号是有可能的。考虑到实际系统不可能工作在最大处理速度下,假定只能达到最大速度的1/3,则采用时分复用后,至少也能同时处理10路以上的信号。
另一方面,由于每一路分路滤波器(包括同相支路和正交支路)都采用64阶FIR低通滤波器,其带宽、过渡带带宽和阻带衰减完全相同,也就是说冲激响应完全相同,所以构成FIR滤波器的矢量乘法器可以重复利用。每一路输出低通滤波器也都具有相同的电路结构。在原理上,它与分路滤波器完全相同,因此这里只以分路滤波器为例进行讨论。FIR滤波器主要由移位寄存器、相加器及矢量乘法器构成?2,其中矢量乘法器在FIR滤波器中占用了大部分硬件资源。因此,节省矢量乘法器,便可以节省系统资源。由此可见,时分复用的实质是指矢量乘法器的时分复用。
下面以实例说明时分复用的实现方法。
为讨论方便,假定FIR滤波器的阶数为8阶,时分复用的路数k=2。设FIR滤波器的冲激响应为h?n ,第一路输入信号为x1?n ,第二路输入信号为x2?n ,滤波器的工作频率为2倍输入数据率。两路信号经复合器形成组合信号,其时序如图3所示。

由图3可以看出,复合器输出的组合信号实际上是将第一路信号和第二路信号进行了交织,在奇数时刻出现的为第一路信号,在偶数时刻出现的为第二路信号。为使同一路信号同时从移位相加器中输出到矢量乘法器,必须保证在奇数时刻移位相加器输出的信号都为第一路信号,而偶数时刻输出的信号都为第二路信号。此外还要保证两路数据都能够在时钟的控制下顺序移位。为了满足上述条件,设计了两路信号复用的FIR滤波器,其结构框图如图4所示。

该滤波器只是在8阶FIR滤波器的基础上增加了8个移位寄存器?3,正是这8个移位寄存器使得矢量乘法器计算第一路信号时,第二路信号得以缓存;而在下一时刻到来时,才将第二路信号输出给矢量乘法器。这样就完成了两路信号的同时滤波。滤波后的信号仍以交织的形式输出,可利用分路器将它们分开。
同理,如果同时进行k路滤波,则滤波器中移位寄存器的个数将是单路FIR滤波器中移位寄存器个数的k倍。即假定FIR滤波器的阶数为N,则单路滤波器需要移位寄存器的个数为N,k路滤波器需要的移位寄存器个数为k·N。 另外,值得注意的是:采用时分复用方法后,整个系统就工作于不同的时钟频率下。假定系统采样频率为fs,进行时分复用后同时处理k路信号,则非时分复用部分的时钟频率为fs,时分复用部分的时钟频率为k·fs为使系统能够正常工作,还要在系统中加上时钟和控制电路,以控制系统的时钟和同步。图5给出了分路滤波器的时分复用框图。

利用MAX+plusII对两路信号复用滤波器的AHDL源代码进行编译,发现两路信号复用滤波器比单路滤波器多用的硬件资源不到单路硬件资源的20%。所以说,利用时分复用的方法达到了预期目标。
这种基于FPGA的数字式解调器的优点是容易和计算机相结合形成数字式FM-FM遥测数据处理系统。一方面,遥测数据可以传送给计算机,进行存储、分析和显示;另一方面,计算机也可以给数字式解调器加载不同的程序,以改变解调器的参数设置,使之适合于IRIG的全部标准。
但是,该数字式解调器仍有其不足之处,即运算精度不够高,因为利用FPGA难以进行浮点运算。如果滤波器用FPGA实现,数据宽度取12bit,鉴频器用DSP实现,采用浮点运算,则系统精度必会得到改善,但付出的代价是系统复杂度增加。

 举报
举报







 举报
举报

