1 引言
随着现代通信领域中技术发展的突飞猛进,整机系统对模数转换提出了更高的要求。例如软件无线电系统,其中的关键问题就是模数转换电路的高速(即高转换速率或高采样频率)、高分辨率(即高转换位数)等性能要求的实现 。在高速领域,现有的模数转换以并行转换为主,但是由于其电路规模随着分辨率的提高而呈指数式的增长(即2N -1,N为转换位数)以及由2N-1 个比较器的亚稳态 和失配而引起的闪烁码所造成的输出不稳定,很难实现8位以上的高分辨率,而且功耗和体积较大,难以满足实际使用的要求 。针对并行模数转换的局限,本文提出了一种采用分段量化和比特滑动技术的流水并行式模数转换电路,较好地结合了并行式和逐次逼近比较式两种模数转换各自的长处,在保证高速工作的同时,可实现并行式难以实现的8位以上的高分辨率模数转换,而且比现有的流水并行式模数转换电路[3,4]更进一步简化结构、减少寄存器数量、降低功耗,更有利于集成化。
假设对任意波形信号在某一时刻采样值 A0进行n位的二进制量化结果为: D1D2…Dn ,则A0可以表示为:A0=VR(D1+D-2+…+2-(n-1)Dn)+δn(1)其中,是A0经过 n位二进制量化后的量化误差,D1 是A0与VR相比较的结果: D1=1 A0VR0A0VR将其适当变形后可得:A0=VRD1+VR(2-1+…+2-(n-1)Dn)+δn(2)
将(2)式中的2-1D 2移至等式的左边,然后等式两边同时乘以2得:重复上述过程可得: A1=2(A0-VRD1)=VRD2+VR(2-1D3+…+2-(n-2)Dn)+22+δn(3)重复上述过程可得:A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-3)Dn)+22δnAn=2(An-1-VRDN)=2nδn(4)
其中,Di+1 是Ai与VR相比较的结果:Di+1=1AVR0AVR i=0,1,n-1(5)Ai+1=2(Ai-VRDi+1)(6)现再假设对A0进行 k位的二进制量化(2≤k?????? A0=VR(d1+2-1d2+…+2-(n-1)dk)+δk(7)
其中,δk是A0经过 k位二进制量化后的量化误差,重复上述过程可得:A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-2)dk)+2δkAk=2(Ak-1-VRDN)=2kδk(8)
其中,di+1是与 VR相比较的结果(i=0,1,…, k-1。)。然后再设对Ak进行n -k位的二进制量化的结果为:dk+ 1dk+2…d n,则Ak又可以表示为: Ak=VR(d=+1+2-1dk+2+…+2-(n-2)dn)+δn
其中,是经过n-k位二进制量化后的量化误差,重复上述过程可得:
Ak+1=2(Ak--VRdk+1)=VRD2+VR(2-1D4+…+2-(n-2)dk)+2δnAn=2(An-1-VRdn)=2(n-k) δn
其中,di+1 是与VR相比较的结果(i=k ,k+1…,n-1。)。
由(2)、(7)两式可得,D 1和d1都是A0 与VR相比较的结果,因此有:d 1=D1。再由(3)、(8)两式可得:。如此一直递推下去,最后可得:d2= D2,,…,dn=D n,,。这样就证明了对任意波形信号电压A 0进行一次n位二进制量化和i次分段 ni位二进制量化(∑ni=n)是等效的,而且,其模拟余量A n也可以用于扩展模数转换的量化比特数(即提高转换的分辨率)。 因此,完全可以将模拟信号先经过位数较少的模数转换电路进行粗转换,然后将其模拟余量再送入多位高速并行模数转换电路进行高速、高分辨率的模数转换。
现有流水并行式模数转换就是将延迟逐次比较式A/D转换电路在时间上的串行工作转化为单个模块的流水式串行工作,对输入信号进行粗转换,然后再采用多位高速并行模数转换电路对粗转换的模拟余量进行高速、高分辨率的模数转换。
在12位流水并行式模数转换电路 中,转换时间为:
t31c=t1c=t3ctCA+tSH(9)而与位数 n无关。其中,t31C是整个模数转换电路的转换时间,t1C是8位并行模数转换电路的转换时间,t3C是流水式电路的转换时间, tCA是流水式电路的比较单元CA的延迟时间, tSH是流水式电路的采样保持单元SH的采样保持时间。这种模数转换电路由于受到tCA和tSH 的限制,转换速率难以进一步提高。
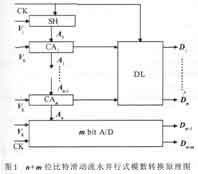
为了提高转换速率,就得设法减少t CA 或tSH,本文提出一种比特滑动流水并行模数转换方法,将 12位流水并行式模数转换电路中的采样保持单元全部省去, 然后在CA1之前加上一个采样保持单元SH,并且采样保持单元SH及各个比较单元CA 1~CAn内部均采用超高速器件,其转换原理如图1所示。只要所设计的比较单元CA1~CAn 和采样保持单元SH满足以下条件:
tCA<1/n*tSH(10)
则CA1~CAn 就能在SH保持时间内快速完成n位逐次比较。因而,转换时间变为:
T31C=T1C=T3CTSH(11)
而在tSH时间内与 tCA无关,从而可以提高转换速率,并且节省了器件、减少了电路规模和功耗。至于n的大小可根据转换速度和分辨率的要求、比较单元和采样保持单元的延迟时间和器件成本等实际应用因素来设定,因而称之为比特滑动。
比特滑动流水并行式模数转换方法的转换过程是,首先将输入的模拟电压Vi经过SH采样保持为 A0,然后经过CA1~CAn 逐级比较,得到n位数字转换结果,并送锁存器DL,在时钟控制下同时输出D1~Dn 。最后,输出模拟余量An到m位并行AD 转换器,继续进行转换,并在时钟控制下输出m位数字输出 Dn+1~Dn +m,从而完成n+m位高速高分辨率模数转换。
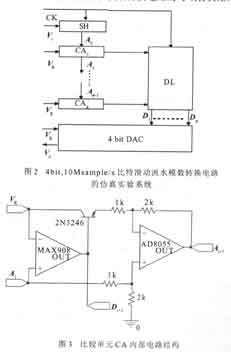
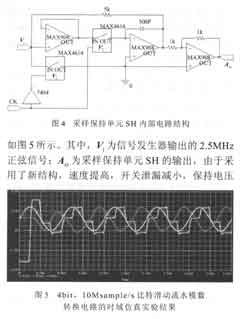
采用如上所述原理,设计了一个4位比特滑动流水模数转换电路,并进行了PSPICE仿真。其仿真电路系统如图2所示。其中,比较单元CA由比较器MAX908和运算放大器AD8055组成,其内部电路结构如图3所示, tCA达到8ns;采样保持单元SH由模拟开关MAX4614和运算放大器AD8055 组成,其内部电路结构如图4所示,tSH 达到100ns,是能克服美国AD公司采样保持电路AD585缺陷且性能优于AD585的新结构SH电路,新SH电路的捕捉时间t AC=40ns、孔径时间tAP=10ns。以上这些都满足(10)式的要求,因此,根据(11)式转换时间 t3C可取100ns。
4位比特滑动流水模数转换电路的时域仿真结果如图5所示。其中,VI 为信号发生器输出的2.5MHz正弦信号;AO 为采样保持单元SH的输出,由于采用了新结构,速度提高,开关泄漏减小,保持电压的跌落变化率减小,精度提高; VO为4 位数模转换器的模拟输出。图5的仿真结果表明,本文提出的比特滑动流水模数转换电路工作正常,线性化程度较好,只要按照图1所示电路接入m位并行AD转换器( t1C为50ns),就能构成4+m位模数转换器。
1 引言
随着现代通信领域中技术发展的突飞猛进,整机系统对模数转换提出了更高的要求。例如软件无线电系统,其中的关键问题就是模数转换电路的高速(即高转换速率或高采样频率)、高分辨率(即高转换位数)等性能要求的实现 。在高速领域,现有的模数转换以并行转换为主,但是由于其电路规模随着分辨率的提高而呈指数式的增长(即2N -1,N为转换位数)以及由2N-1 个比较器的亚稳态 和失配而引起的闪烁码所造成的输出不稳定,很难实现8位以上的高分辨率,而且功耗和体积较大,难以满足实际使用的要求 。针对并行模数转换的局限,本文提出了一种采用分段量化和比特滑动技术的流水并行式模数转换电路,较好地结合了并行式和逐次逼近比较式两种模数转换各自的长处,在保证高速工作的同时,可实现并行式难以实现的8位以上的高分辨率模数转换,而且比现有的流水并行式模数转换电路[3,4]更进一步简化结构、减少寄存器数量、降低功耗,更有利于集成化。
假设对任意波形信号在某一时刻采样值 A0进行n位的二进制量化结果为: D1D2…Dn ,则A0可以表示为:A0=VR(D1+D-2+…+2-(n-1)Dn)+δn(1)其中,是A0经过 n位二进制量化后的量化误差,D1 是A0与VR相比较的结果: D1=1 A0VR0A0VR将其适当变形后可得:A0=VRD1+VR(2-1+…+2-(n-1)Dn)+δn(2)
将(2)式中的2-1D 2移至等式的左边,然后等式两边同时乘以2得:重复上述过程可得: A1=2(A0-VRD1)=VRD2+VR(2-1D3+…+2-(n-2)Dn)+22+δn(3)重复上述过程可得:A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-3)Dn)+22δnAn=2(An-1-VRDN)=2nδn(4)
其中,Di+1 是Ai与VR相比较的结果:Di+1=1AVR0AVR i=0,1,n-1(5)Ai+1=2(Ai-VRDi+1)(6)现再假设对A0进行 k位的二进制量化(2≤k?????? A0=VR(d1+2-1d2+…+2-(n-1)dk)+δk(7)
其中,δk是A0经过 k位二进制量化后的量化误差,重复上述过程可得:A1=2(A0-VRD1)=VRD2+VR(2-1D4+…+2-(n-2)dk)+2δkAk=2(Ak-1-VRDN)=2kδk(8)
其中,di+1是与 VR相比较的结果(i=0,1,…, k-1。)。然后再设对Ak进行n -k位的二进制量化的结果为:dk+ 1dk+2…d n,则Ak又可以表示为: Ak=VR(d=+1+2-1dk+2+…+2-(n-2)dn)+δn
其中,是经过n-k位二进制量化后的量化误差,重复上述过程可得:
Ak+1=2(Ak--VRdk+1)=VRD2+VR(2-1D4+…+2-(n-2)dk)+2δnAn=2(An-1-VRdn)=2(n-k) δn
其中,di+1 是与VR相比较的结果(i=k ,k+1…,n-1。)。
由(2)、(7)两式可得,D 1和d1都是A0 与VR相比较的结果,因此有:d 1=D1。再由(3)、(8)两式可得:。如此一直递推下去,最后可得:d2= D2,,…,dn=D n,,。这样就证明了对任意波形信号电压A 0进行一次n位二进制量化和i次分段 ni位二进制量化(∑ni=n)是等效的,而且,其模拟余量A n也可以用于扩展模数转换的量化比特数(即提高转换的分辨率)。 因此,完全可以将模拟信号先经过位数较少的模数转换电路进行粗转换,然后将其模拟余量再送入多位高速并行模数转换电路进行高速、高分辨率的模数转换。
现有流水并行式模数转换就是将延迟逐次比较式A/D转换电路在时间上的串行工作转化为单个模块的流水式串行工作,对输入信号进行粗转换,然后再采用多位高速并行模数转换电路对粗转换的模拟余量进行高速、高分辨率的模数转换。
在12位流水并行式模数转换电路 中,转换时间为:
t31c=t1c=t3ctCA+tSH(9)而与位数 n无关。其中,t31C是整个模数转换电路的转换时间,t1C是8位并行模数转换电路的转换时间,t3C是流水式电路的转换时间, tCA是流水式电路的比较单元CA的延迟时间, tSH是流水式电路的采样保持单元SH的采样保持时间。这种模数转换电路由于受到tCA和tSH 的限制,转换速率难以进一步提高。
为了提高转换速率,就得设法减少t CA 或tSH,本文提出一种比特滑动流水并行模数转换方法,将 12位流水并行式模数转换电路中的采样保持单元全部省去, 然后在CA1之前加上一个采样保持单元SH,并且采样保持单元SH及各个比较单元CA 1~CAn内部均采用超高速器件,其转换原理如图1所示。只要所设计的比较单元CA1~CAn 和采样保持单元SH满足以下条件:

tCA<1/n*tSH(10)
则CA1~CAn 就能在SH保持时间内快速完成n位逐次比较。因而,转换时间变为:
T31C=T1C=T3CTSH(11)
而在tSH时间内与 tCA无关,从而可以提高转换速率,并且节省了器件、减少了电路规模和功耗。至于n的大小可根据转换速度和分辨率的要求、比较单元和采样保持单元的延迟时间和器件成本等实际应用因素来设定,因而称之为比特滑动。
比特滑动流水并行式模数转换方法的转换过程是,首先将输入的模拟电压Vi经过SH采样保持为 A0,然后经过CA1~CAn 逐级比较,得到n位数字转换结果,并送锁存器DL,在时钟控制下同时输出D1~Dn 。最后,输出模拟余量An到m位并行AD 转换器,继续进行转换,并在时钟控制下输出m位数字输出 Dn+1~Dn +m,从而完成n+m位高速高分辨率模数转换。
采用如上所述原理,设计了一个4位比特滑动流水模数转换电路,并进行了PSPICE仿真。其仿真电路系统如图2所示。其中,比较单元CA由比较器MAX908和运算放大器AD8055组成,其内部电路结构如图3所示, tCA达到8ns;采样保持单元SH由模拟开关MAX4614和运算放大器AD8055 组成,其内部电路结构如图4所示,tSH 达到100ns,是能克服美国AD公司采样保持电路AD585缺陷且性能优于AD585的新结构SH电路,新SH电路的捕捉时间t AC=40ns、孔径时间tAP=10ns。以上这些都满足(10)式的要求,因此,根据(11)式转换时间 t3C可取100ns。


4位比特滑动流水模数转换电路的时域仿真结果如图5所示。其中,VI 为信号发生器输出的2.5MHz正弦信号;AO 为采样保持单元SH的输出,由于采用了新结构,速度提高,开关泄漏减小,保持电压的跌落变化率减小,精度提高; VO为4 位数模转换器的模拟输出。图5的仿真结果表明,本文提出的比特滑动流水模数转换电路工作正常,线性化程度较好,只要按照图1所示电路接入m位并行AD转换器( t1C为50ns),就能构成4+m位模数转换器。

 举报
举报





 举报
举报

