1. Buck 电路的模型
Buck 电路是最常见的电路,具体电路结构如图所示。
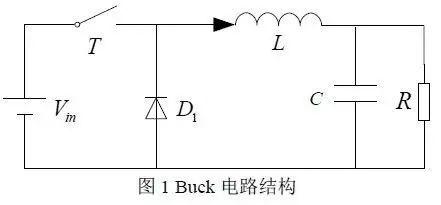
对其进行等效,得到的等效电路如图 2 所示:
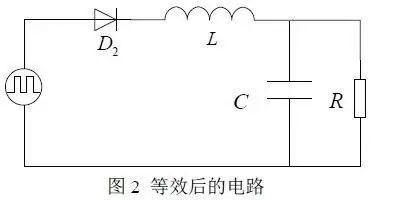
对图 1 进行等效后得到徒图 2 电路,可以看出相当于一个脉冲波形的输出,高电压幅值为 Vin,即图 1 输入直流的电压值,低电压为 0。由于图 1 中 D1 的存在,使得电流只能单向流动,因此在图 2 中等效为串联二极管 D2。
2. Buck 电路的常规角度分析
2.1 时域分析方法
下面按着电容充放电和电感充放电进行时域分析。
时域分析的过程是按着输入电压的高与低,分析电路里电容电压和电感电流的变化过程。这个分析过程可以按着大多课本上面所讲述的过程分析,从 CCM 模式到 DCM 模式。
(1)CCM 模式
当输入电压为 Vin 时,电感电流增加,电流小于输出负载电流 iL,此时的负载电流由电感和电容同时提供。当电流逐渐增加到大于输出的平均电流的时候,电感电流为负载和电容提供能量。当输入为 0,即开关管关断时,电感电流下降,此时电流依然大于输出平均值,电容电压延续上述上升的趋势,直至电感电流小于输出平均电流,电容开始放电,完成一个开关周期的循环过程。
具体的波形如下:

(2)DCM 模式
在 DCM 模式下,电感的电流在开关管管断后的一段时间后逐渐减为零,此时的等效输入电压为输出电压值,具体的波形如图 4 所示。
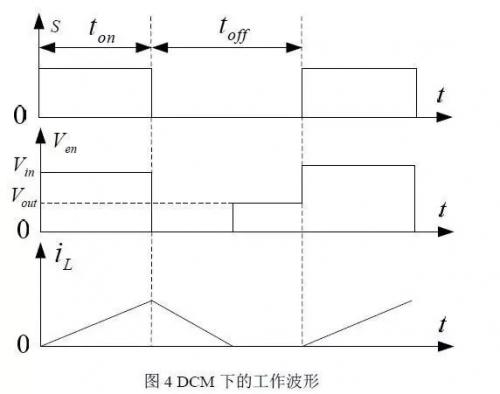
在CCM 模式下,电压的输出值与输入值之间是正比关系,比例系数为占空比 D。在 DCM 的模式下电压会被抬升,具体的关系和电路的参数、开关频率以
及占空比相关。具体的推导关系为:

其中
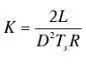
根据此公式可以看出,当电路输出开路,即电阻无穷大的时候,输入等于输出。
2.2 相平面分析
上面的分析过程中,电感电流以及电容的电压都被看作是三角波的上升和下降,其实在有些过程中这些状态变量是正弦变化的,下面从相平面的方式分析它的工作过程。
(1)CCM 模式
CCM模式下的电路的相平面图为图 5 所示,红色部分为电感电流和电容电压的变化范围和变化过程。
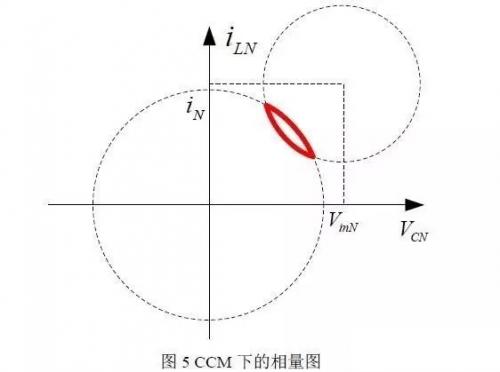
图中的过程和上面的分析过程是相似的,只是在前面把电感电流和电容电压的变化都看作是线性的。其实质的变化是电感和电容的谐振。后面将其与经典并联负载谐振的电路进行比较可以有更深层次的理解。
(2)DCM 模式
在 DCM 模式下,电路的向量图为图 6 所示,同样变化过程如图中的红色部分所示。
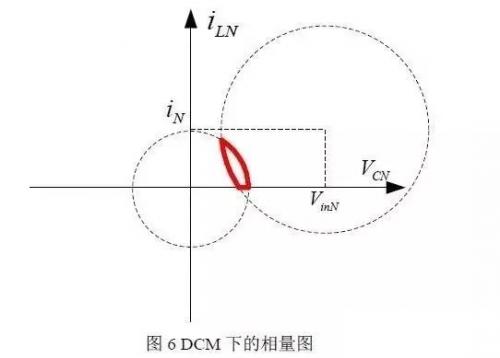
图中的红色部分表示状态变量的变化过程,中间有一段是电流为零的,此时的电容电压逐渐下降,所有的变化过程也不是前面所述的线性变化的关系。
对于两种模式,图形都是瘦长的,开关频率远大于谐振频率。对于 PWM 调制的方式,不同的占空比改变的是谐振的半径,即红色部分在空间的位置,其基本形状不会发生大的改变,因为开关频率是一定的,红色部分对应的时间也就是一个恒定的值。于是对于既定的电路参数,改变占空比可能导致系统进入 DCM 模式(参考图 6)。
3. Buck 电路的滤波器角度分析
3.1 典型二阶滤波器
二阶滤波器的电路如图 7 所示,与 Buck 电路的后半部分唯一的不同是,Buck 电路只允许电流的单向流动,下面首先对一般的滤波器进行分析。

推导其电压传递函数为:
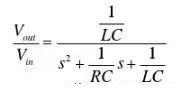
总体的阻抗为:
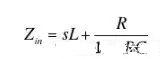
从上面传递函数(1)可以看出:自然频率大小等于其谐振频率,在负载一定的前提下,电容的大小影响二阶系统的阻尼系数,即系统的系统的响应速度和超调。系统低频的增益为 1,高频 40dB/dec 下降,对高频分量的衰减效果很好,转折频率为谐振频率。
从上面的传递函数(3)可以看出:在负载一定的情况下,增大系统的电感值,可以使得系统的阻抗增加,即在输入电压一定的情况下,得到的纹波电流就越小。
3.2 电流单向二阶滤波器
当在此典型滤波器的输入限制为电流单向流动,如图 8 所示在输入端加上二极管,会有不同的结果,也就是说此时的二阶滤波不在是滤波作用,而是一个整流器电路。
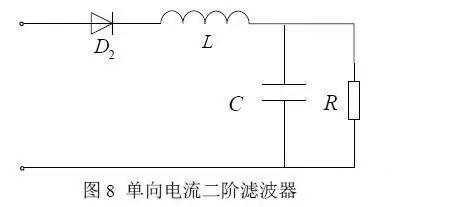
由于二极管的存在使得电流只能单向流动,电压为正时,电流正向流动,电压为负值时,电流逐渐减为零不再反向,电压和电流并不同相位。
具体的电路相量图如图 9 所示,开通部分与 Buck 电路的开通部分相同,关断后电压反向的过程如图所示,与图 6 所示的 0 电压不同。这样也就说明了一个问题,这种形式的滤波器的效果与 DCM 模式的 Buck 模式是类似的,虽然细节是不同的。也就说明一根问题:电流单向的滤波器输出结果与输入电压单向的完整滤波器结果是不同的。
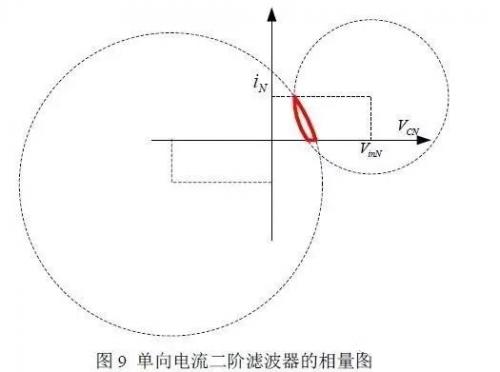
根据此图可以看出电容的电压为一个正值,相当于整流电路的效果。
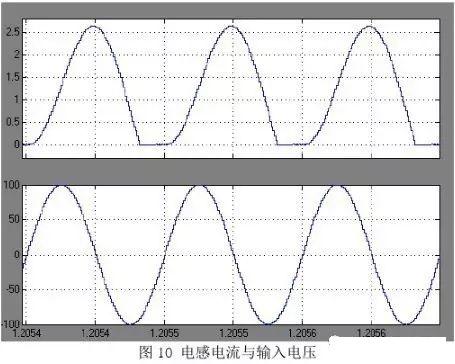
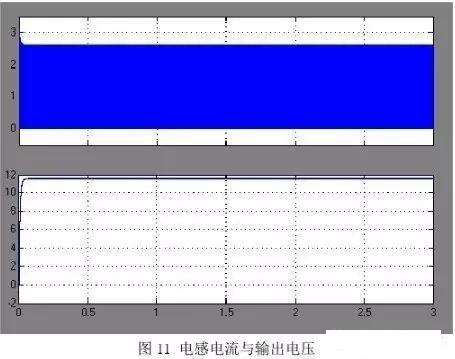
下面给出比较图:图 10 是交流输入,电流单向的输出效果。上面为电感电流下面为输入电压值,可以看出二者相位不同。图 11 上面为电感电流,下面是输出电压值。可以看出输出是恒压效果。
这个系统为典型的二阶滤波环节,下面分析其与 Buck 电路后级的相同之处和不同之处。
首先说明,对于 Buck 电路如图 2 所示的输入电压可以等效为一个直流分量和一个交流量的加和。对于直流分量在滤波器的输出侧增益为 1 且电流为正向,下面主要针对交流分量分析其输出效果。
(1)CCM 模式
CCM 模式下的 Buck 电路电流连续,相当于后级为经典滤波器,交流分量的效果叠加在恒流和恒压的输出上,也就是我们看到的电容电压和电感电流上有一定的纹波。此纹波值是输入电压交流分量经过完整滤波器的效果,这样理解的原因是:电感电流始终连续。
此时输出的的电感电流的波形为图 12 所示那样,平均电流 io 为直流分量的效果,纹波值为交流分量的效果。

(2)DCM 模式
DCM 模式下,交流分量的叠加不再完整,即不再是完整滤波器效果,此时的结果相当于后级为部分电流单向流动的滤波器,具体分析可以根据下图 13 看出。首先假设电感电流可以反向,则此时的电感电流为图 13 中的 a)所示,图中的虚线部分 io 依然是直流成分的效果,交流成分的效果依然是零,即如图中 b)所示那样。如果电流限制为单向,此时的效果图如 c)所示,平均输出电流 io 值不再是单独的直流成分的效果,而是交直流效果之和。交流成分的平均效果如图 d)所示,会有一个平均值叠加在直流成分上,这也就是为什么 DCM 模式下的 Buck 电路的电压会升高。
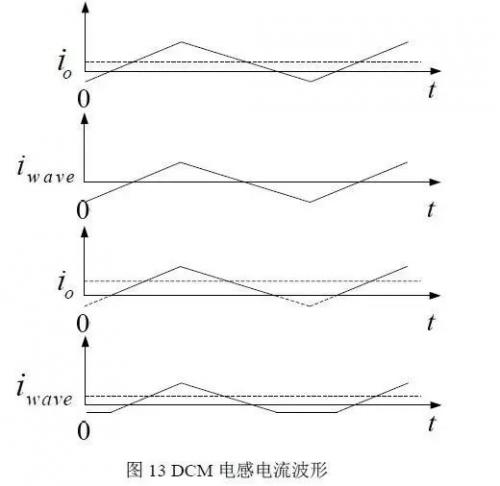
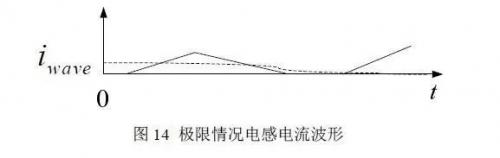
在输出电阻为无穷大的时候,平均输出电流零,直流成分也为零,其变化过程为图 14 所示虚线部分为输出电流平均值,随着时间的推移逐渐减为零。此时输出电压等于输入电压。
4. Buck 电路与并联负载谐振
4.1 并联负载谐振的等效电路
并联的负载谐振电路一般有两种形式,即输出整流侧电压源形式和输出电流源形式,具体的电路拓扑结构如图 15 和图 16 所示。
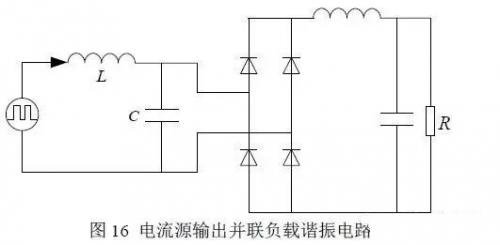
对于这两种形式的电路而言,都可以等效为图 17 所示的电路。
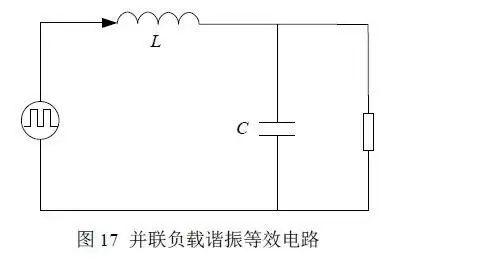
对于图 15 所示的电路,输出侧等效为电压源,正常工作的时候谐振电容两端的电压是削顶的正弦波,而一个周期内的电感电流是正弦变化和线性变化的组合,对其进行等效有一定的困难。
现在主要针对第二种形式输出电流源形式的并联负载谐振电路进行等效分析。首先说明一个相关的问题,即图 15 所示电路的不控整流部分,输入端是电容两端的电压,电网电压整流是不同的,电网电压的正弦变化是不会改变的,始终是正弦的,此电路中的电压波形会被削顶。
对于图 16 所示的电路,输出侧是电流源形式,主要针对电感电流连续的工作模式。谐振电容的电压是正弦变化的,只要电容两端的电压不为零,便会有电流从谐振部分流入整流输出部分,如图 18 所示。
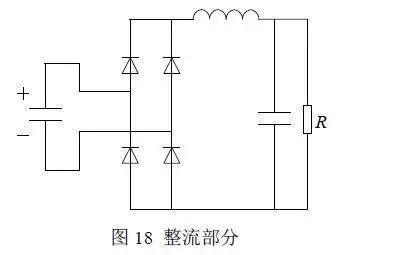
只要电容的电压不为零,整流的二极管便是对角开通,不会出现电感续流的过程。后级的电感和电容是二阶滤波器,即相当于 Buck 电路的输出侧,输出为整流电压的直流成分。由于输入电压为谐振电容电压的绝对值,积分求平均后可以得到:

其中的 Vcp 是电容电压的峰值。流过电阻的电流为:

则整流输入侧的电流为:
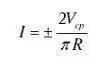
取其基波成分为:

这样得到的等效电阻为:

这样就得到的了输出电压与谐振电容电压峰值之间的关系以及等效电阻值,即可得到图 17 所示的等效电路形式,这样便可以求的其增益曲线。
4.2 Buck 电路与并联负载谐振
根据图 17 可以看出,此图为二阶滤波器,不是 Buck 电路的输出部分。即使在谐振电感电流断续的模式下,也与 Buck 电路的电流断续模式不同。
对于电路的后半部分,即输出恒流的部分是可以按着 Buck 电路的连续模式等效分析的。
1. Buck 电路的模型
Buck 电路是最常见的电路,具体电路结构如图所示。

对其进行等效,得到的等效电路如图 2 所示:

对图 1 进行等效后得到徒图 2 电路,可以看出相当于一个脉冲波形的输出,高电压幅值为 Vin,即图 1 输入直流的电压值,低电压为 0。由于图 1 中 D1 的存在,使得电流只能单向流动,因此在图 2 中等效为串联二极管 D2。
2. Buck 电路的常规角度分析
2.1 时域分析方法
下面按着电容充放电和电感充放电进行时域分析。
时域分析的过程是按着输入电压的高与低,分析电路里电容电压和电感电流的变化过程。这个分析过程可以按着大多课本上面所讲述的过程分析,从 CCM 模式到 DCM 模式。
(1)CCM 模式
当输入电压为 Vin 时,电感电流增加,电流小于输出负载电流 iL,此时的负载电流由电感和电容同时提供。当电流逐渐增加到大于输出的平均电流的时候,电感电流为负载和电容提供能量。当输入为 0,即开关管关断时,电感电流下降,此时电流依然大于输出平均值,电容电压延续上述上升的趋势,直至电感电流小于输出平均电流,电容开始放电,完成一个开关周期的循环过程。
具体的波形如下:

(2)DCM 模式
在 DCM 模式下,电感的电流在开关管管断后的一段时间后逐渐减为零,此时的等效输入电压为输出电压值,具体的波形如图 4 所示。

在CCM 模式下,电压的输出值与输入值之间是正比关系,比例系数为占空比 D。在 DCM 的模式下电压会被抬升,具体的关系和电路的参数、开关频率以
及占空比相关。具体的推导关系为:

其中
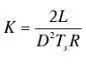
根据此公式可以看出,当电路输出开路,即电阻无穷大的时候,输入等于输出。
2.2 相平面分析
上面的分析过程中,电感电流以及电容的电压都被看作是三角波的上升和下降,其实在有些过程中这些状态变量是正弦变化的,下面从相平面的方式分析它的工作过程。
(1)CCM 模式
CCM模式下的电路的相平面图为图 5 所示,红色部分为电感电流和电容电压的变化范围和变化过程。

图中的过程和上面的分析过程是相似的,只是在前面把电感电流和电容电压的变化都看作是线性的。其实质的变化是电感和电容的谐振。后面将其与经典并联负载谐振的电路进行比较可以有更深层次的理解。
(2)DCM 模式
在 DCM 模式下,电路的向量图为图 6 所示,同样变化过程如图中的红色部分所示。

图中的红色部分表示状态变量的变化过程,中间有一段是电流为零的,此时的电容电压逐渐下降,所有的变化过程也不是前面所述的线性变化的关系。
对于两种模式,图形都是瘦长的,开关频率远大于谐振频率。对于 PWM 调制的方式,不同的占空比改变的是谐振的半径,即红色部分在空间的位置,其基本形状不会发生大的改变,因为开关频率是一定的,红色部分对应的时间也就是一个恒定的值。于是对于既定的电路参数,改变占空比可能导致系统进入 DCM 模式(参考图 6)。
3. Buck 电路的滤波器角度分析
3.1 典型二阶滤波器
二阶滤波器的电路如图 7 所示,与 Buck 电路的后半部分唯一的不同是,Buck 电路只允许电流的单向流动,下面首先对一般的滤波器进行分析。

推导其电压传递函数为:
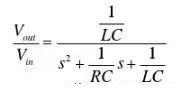
总体的阻抗为:
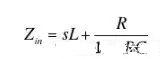
从上面传递函数(1)可以看出:自然频率大小等于其谐振频率,在负载一定的前提下,电容的大小影响二阶系统的阻尼系数,即系统的系统的响应速度和超调。系统低频的增益为 1,高频 40dB/dec 下降,对高频分量的衰减效果很好,转折频率为谐振频率。
从上面的传递函数(3)可以看出:在负载一定的情况下,增大系统的电感值,可以使得系统的阻抗增加,即在输入电压一定的情况下,得到的纹波电流就越小。
3.2 电流单向二阶滤波器
当在此典型滤波器的输入限制为电流单向流动,如图 8 所示在输入端加上二极管,会有不同的结果,也就是说此时的二阶滤波不在是滤波作用,而是一个整流器电路。

由于二极管的存在使得电流只能单向流动,电压为正时,电流正向流动,电压为负值时,电流逐渐减为零不再反向,电压和电流并不同相位。
具体的电路相量图如图 9 所示,开通部分与 Buck 电路的开通部分相同,关断后电压反向的过程如图所示,与图 6 所示的 0 电压不同。这样也就说明了一个问题,这种形式的滤波器的效果与 DCM 模式的 Buck 模式是类似的,虽然细节是不同的。也就说明一根问题:电流单向的滤波器输出结果与输入电压单向的完整滤波器结果是不同的。

根据此图可以看出电容的电压为一个正值,相当于整流电路的效果。
下面给出比较图:图 10 是交流输入,电流单向的输出效果。上面为电感电流下面为输入电压值,可以看出二者相位不同。图 11 上面为电感电流,下面是输出电压值。可以看出输出是恒压效果。


这个系统为典型的二阶滤波环节,下面分析其与 Buck 电路后级的相同之处和不同之处。
首先说明,对于 Buck 电路如图 2 所示的输入电压可以等效为一个直流分量和一个交流量的加和。对于直流分量在滤波器的输出侧增益为 1 且电流为正向,下面主要针对交流分量分析其输出效果。
(1)CCM 模式
CCM 模式下的 Buck 电路电流连续,相当于后级为经典滤波器,交流分量的效果叠加在恒流和恒压的输出上,也就是我们看到的电容电压和电感电流上有一定的纹波。此纹波值是输入电压交流分量经过完整滤波器的效果,这样理解的原因是:电感电流始终连续。
此时输出的的电感电流的波形为图 12 所示那样,平均电流 io 为直流分量的效果,纹波值为交流分量的效果。

(2)DCM 模式
DCM 模式下,交流分量的叠加不再完整,即不再是完整滤波器效果,此时的结果相当于后级为部分电流单向流动的滤波器,具体分析可以根据下图 13 看出。首先假设电感电流可以反向,则此时的电感电流为图 13 中的 a)所示,图中的虚线部分 io 依然是直流成分的效果,交流成分的效果依然是零,即如图中 b)所示那样。如果电流限制为单向,此时的效果图如 c)所示,平均输出电流 io 值不再是单独的直流成分的效果,而是交直流效果之和。交流成分的平均效果如图 d)所示,会有一个平均值叠加在直流成分上,这也就是为什么 DCM 模式下的 Buck 电路的电压会升高。

在输出电阻为无穷大的时候,平均输出电流零,直流成分也为零,其变化过程为图 14 所示虚线部分为输出电流平均值,随着时间的推移逐渐减为零。此时输出电压等于输入电压。

4. Buck 电路与并联负载谐振
4.1 并联负载谐振的等效电路
并联的负载谐振电路一般有两种形式,即输出整流侧电压源形式和输出电流源形式,具体的电路拓扑结构如图 15 和图 16 所示。

对于这两种形式的电路而言,都可以等效为图 17 所示的电路。

对于图 15 所示的电路,输出侧等效为电压源,正常工作的时候谐振电容两端的电压是削顶的正弦波,而一个周期内的电感电流是正弦变化和线性变化的组合,对其进行等效有一定的困难。
现在主要针对第二种形式输出电流源形式的并联负载谐振电路进行等效分析。首先说明一个相关的问题,即图 15 所示电路的不控整流部分,输入端是电容两端的电压,电网电压整流是不同的,电网电压的正弦变化是不会改变的,始终是正弦的,此电路中的电压波形会被削顶。
对于图 16 所示的电路,输出侧是电流源形式,主要针对电感电流连续的工作模式。谐振电容的电压是正弦变化的,只要电容两端的电压不为零,便会有电流从谐振部分流入整流输出部分,如图 18 所示。

只要电容的电压不为零,整流的二极管便是对角开通,不会出现电感续流的过程。后级的电感和电容是二阶滤波器,即相当于 Buck 电路的输出侧,输出为整流电压的直流成分。由于输入电压为谐振电容电压的绝对值,积分求平均后可以得到:

其中的 Vcp 是电容电压的峰值。流过电阻的电流为:

则整流输入侧的电流为:
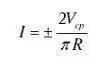
取其基波成分为:

这样得到的等效电阻为:

这样就得到的了输出电压与谐振电容电压峰值之间的关系以及等效电阻值,即可得到图 17 所示的等效电路形式,这样便可以求的其增益曲线。
4.2 Buck 电路与并联负载谐振
根据图 17 可以看出,此图为二阶滤波器,不是 Buck 电路的输出部分。即使在谐振电感电流断续的模式下,也与 Buck 电路的电流断续模式不同。
对于电路的后半部分,即输出恒流的部分是可以按着 Buck 电路的连续模式等效分析的。

 举报
举报






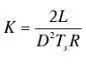



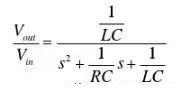
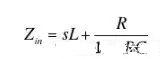











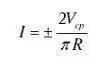



 举报
举报

