因为1/f噪声随着频率降低而提高,所以直流电路具有无限大噪声
虽然直流对电路分析是一个有用的概念,但真实情况是,如果认为直流是工作在0 Hz,那么实际上并不存在这样的事情。随着频率越来越低,趋近0 Hz,周期会越来越长,趋近无限大。这意味着存在一个可以观测的最低频率,哪怕电路在理论上是直流响应。该最低频率取决于采集时长或孔径时间,也就是观测器件输出的时长。如果一名工程师开启器件并观测输出100秒,则其能够观测到的最低频率伪像将是0.01 Hz。这还意味着,此时可以观测到的最低频率噪声也是0.01 Hz。
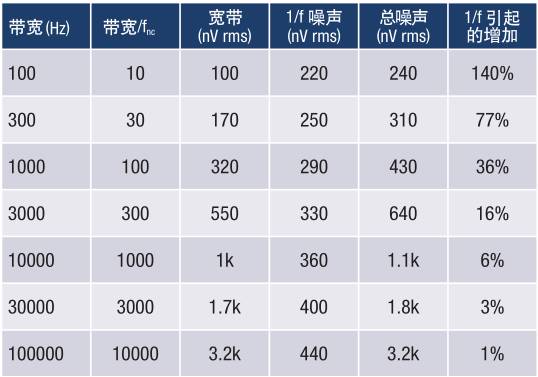
现在通过一个数值例子来展开说明,考虑一个DC至1 kHz电路,连续监控其输出。如果在前100秒观测到电路中一定量的1/f噪声,从0.01 Hz至1 kHz(5个十倍频程的频率),则在30年(约1 nHz,12个十倍频程)中观测到的噪声量可计算为√12/5 = 1.55,或者说比前100秒观测到的噪声多55%。这种增加几乎没有任何意义,即使考虑最差情况——1/f噪声持续增加到1 nHz(目前尚无测量证据)——也是如此。理论上,如果没有明确定义孔径时间,1/f噪声可以计算到一个等于电路寿命倒数的频率。实践中,电路在如此长时间内的偏差以老化效应和长期漂移为主,而不是1/f噪声。许多工程师为直流电路的噪声计算设定0.01 Hz或1 mHz之类的最低频率,以使计算切合实际。
噪声等效带宽会使噪声倍增
噪声等效带宽(NEB)对噪声计算是一个很有用的简化。由于截止频率以上的增益不是0,某些超出电路带宽的噪声会进入电路中。NEB是计算的理想砖墙滤波器的截止频率,它会放入与实际电路相同的噪声量。NEB大于–3 dB带宽,已针对常用滤波器类型和阶数进行计算,例如:对于单极点低通滤波器,它是–3 dB带宽的1.57倍,写成公式就是NEB1-pole = 1.57 × BW3dB。然而,关于应把该乘法因数放在噪声公式中的何处,似乎一直存在混淆。请记住,NEB调节的是带宽,而非噪声,因此应在根号下面,如下式所示:
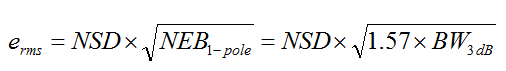
电压噪声最低的放大器是最佳选择
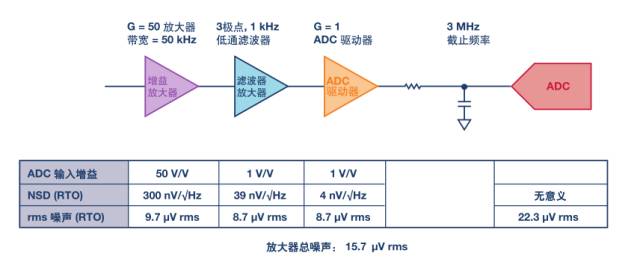
选择运算放大器时,电压噪声常常是设计人员唯一考虑的噪声规格。其实电流噪声同样不能忽略。除非在有输入偏置电流补偿等特殊情况下,电流噪声通常是输入偏置电流的散粒噪声:in = √2 × q × IB。电流噪声通过源电阻转换为电压,因此,如果放大器输入端前面有一个大电阻,那么电流噪声对系统噪声的贡献可能大于电压噪声。电流噪声会成为问题的典型情况是使用低噪声运算放大器且其输入端串联一个大电阻时。例如,考虑低噪声运算放大器ADA4898-1,其输入端串联一个10 kΩ电阻。ADA4898-1的电压噪声为0.9 nV/√Hz,10 kΩ电阻的噪声为12.8 nV/√Hz,2.4 pA/√Hz电流噪声乘以10 kΩ电阻等于24 nV/√Hz,这是系统中的最大噪声源。在类似这种电流噪声占主导地位的情况下,常常可以找到电流噪声较低的器件,从而降低系统噪声;对精密放大器尤其如此,不过高速FET输入运算放大器对高速电路也可能有帮助。例如,若不选择ADA4898-1(从而得不到电压噪声低至0.9 nV/√Hz的好处),可以选择AD8033或ADA4817-1等JFET输入放大器。
在第一级提供大部分增益可实现最佳噪声性能
为了实现更好的噪声性能,常常建议在第一级提供增益,这是对的,因为信号会比随后各级的噪声要大。然而,这样做的缺点是会削弱系统能够支持的最大信号。某些情况下,与其在第一级提供很大一部分增益(虽然这样可以提高测量灵敏度,但会限制动态范围),不如限制第一级提供的增益,并用高分辨率进行数字化处理,使灵敏度和动态范围都达到最大。
给定阻值时,所有类型电阻的噪声相同
电阻的约翰逊噪声非常重要,以至于我们需要一个简单的公式来计算某一电阻在某一温度下的噪声。然而,约翰逊噪声是电阻中可以观测到的最小噪声,而且并非所有类型的电阻都有同等噪声。还有过量噪声,它是电阻中1/f噪声的来源之一,与电阻类型密切相关。过量噪声(有时候也误称为电流噪声)与电流在非连续介质中流动的方式有关。它被规定为噪声指数(NI),单位为dB,以每十倍频程1 µV rms/Vdc为基准。这意味着:如果一个0 dB NI的电阻上有1 Vdc电压,则给定十倍频程时的过量噪声为1 µV rms。碳和厚膜电阻的NI最高,可能高达+10 dB左右,在信号路径的噪声敏感部分中最好避免使用。薄膜电阻一般要好得多,约为–20 dB;金属箔和绕线电阻可以低于–40 dB。
给定足够长的采集时间,均值法可将噪声降至无限小
一般认为均值法可将噪声降低均值数的平方根倍。这在一定条件下是成立的,即NSD必须保持平坦。然而,在1/f范围内和其他几种情况下,这种关系不成立。考虑在一个以恒定频率fs采样的系统中使用均值法,对n个样本求均值并进行1/n抽取,返回m个抽取样本。取n个平均值会将抽取后的有效采样速率变为fs/n,系统看到的有效最大频率降低n倍,白噪声降低√n倍。然而,获得m个样本的时间也会延长n倍,因此系统可以看到的最低频率也会降低n倍(记住,没有0 Hz这种事)。取的均值数越多,频段上的这些最大和最小频率就越往下移。一旦最大和最小频率均在1/f范围内,总噪声便仅取决于这些频率之比,再提高均值数对降低噪声没有进一步的好处。同样的道理也适用于多斜率等积分ADC的长积分时间。除了数学上的限制以外,还存在其他实际限制。例如,若量化噪声是主要噪声源,使得直流输入电压下的ADC输出为一个无闪烁的恒定码,则任何数量的均值都会返回同一个码 。
因为1/f噪声随着频率降低而提高,所以直流电路具有无限大噪声
虽然直流对电路分析是一个有用的概念,但真实情况是,如果认为直流是工作在0 Hz,那么实际上并不存在这样的事情。随着频率越来越低,趋近0 Hz,周期会越来越长,趋近无限大。这意味着存在一个可以观测的最低频率,哪怕电路在理论上是直流响应。该最低频率取决于采集时长或孔径时间,也就是观测器件输出的时长。如果一名工程师开启器件并观测输出100秒,则其能够观测到的最低频率伪像将是0.01 Hz。这还意味着,此时可以观测到的最低频率噪声也是0.01 Hz。
现在通过一个数值例子来展开说明,考虑一个DC至1 kHz电路,连续监控其输出。如果在前100秒观测到电路中一定量的1/f噪声,从0.01 Hz至1 kHz(5个十倍频程的频率),则在30年(约1 nHz,12个十倍频程)中观测到的噪声量可计算为√12/5 = 1.55,或者说比前100秒观测到的噪声多55%。这种增加几乎没有任何意义,即使考虑最差情况——1/f噪声持续增加到1 nHz(目前尚无测量证据)——也是如此。理论上,如果没有明确定义孔径时间,1/f噪声可以计算到一个等于电路寿命倒数的频率。实践中,电路在如此长时间内的偏差以老化效应和长期漂移为主,而不是1/f噪声。许多工程师为直流电路的噪声计算设定0.01 Hz或1 mHz之类的最低频率,以使计算切合实际。
噪声等效带宽会使噪声倍增
噪声等效带宽(NEB)对噪声计算是一个很有用的简化。由于截止频率以上的增益不是0,某些超出电路带宽的噪声会进入电路中。NEB是计算的理想砖墙滤波器的截止频率,它会放入与实际电路相同的噪声量。NEB大于–3 dB带宽,已针对常用滤波器类型和阶数进行计算,例如:对于单极点低通滤波器,它是–3 dB带宽的1.57倍,写成公式就是NEB1-pole = 1.57 × BW3dB。然而,关于应把该乘法因数放在噪声公式中的何处,似乎一直存在混淆。请记住,NEB调节的是带宽,而非噪声,因此应在根号下面,如下式所示:
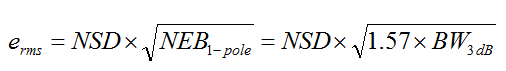
电压噪声最低的放大器是最佳选择
选择运算放大器时,电压噪声常常是设计人员唯一考虑的噪声规格。其实电流噪声同样不能忽略。除非在有输入偏置电流补偿等特殊情况下,电流噪声通常是输入偏置电流的散粒噪声:in = √2 × q × IB。电流噪声通过源电阻转换为电压,因此,如果放大器输入端前面有一个大电阻,那么电流噪声对系统噪声的贡献可能大于电压噪声。电流噪声会成为问题的典型情况是使用低噪声运算放大器且其输入端串联一个大电阻时。例如,考虑低噪声运算放大器ADA4898-1,其输入端串联一个10 kΩ电阻。ADA4898-1的电压噪声为0.9 nV/√Hz,10 kΩ电阻的噪声为12.8 nV/√Hz,2.4 pA/√Hz电流噪声乘以10 kΩ电阻等于24 nV/√Hz,这是系统中的最大噪声源。在类似这种电流噪声占主导地位的情况下,常常可以找到电流噪声较低的器件,从而降低系统噪声;对精密放大器尤其如此,不过高速FET输入运算放大器对高速电路也可能有帮助。例如,若不选择ADA4898-1(从而得不到电压噪声低至0.9 nV/√Hz的好处),可以选择AD8033或ADA4817-1等JFET输入放大器。
在第一级提供大部分增益可实现最佳噪声性能
为了实现更好的噪声性能,常常建议在第一级提供增益,这是对的,因为信号会比随后各级的噪声要大。然而,这样做的缺点是会削弱系统能够支持的最大信号。某些情况下,与其在第一级提供很大一部分增益(虽然这样可以提高测量灵敏度,但会限制动态范围),不如限制第一级提供的增益,并用高分辨率进行数字化处理,使灵敏度和动态范围都达到最大。
给定阻值时,所有类型电阻的噪声相同
电阻的约翰逊噪声非常重要,以至于我们需要一个简单的公式来计算某一电阻在某一温度下的噪声。然而,约翰逊噪声是电阻中可以观测到的最小噪声,而且并非所有类型的电阻都有同等噪声。还有过量噪声,它是电阻中1/f噪声的来源之一,与电阻类型密切相关。过量噪声(有时候也误称为电流噪声)与电流在非连续介质中流动的方式有关。它被规定为噪声指数(NI),单位为dB,以每十倍频程1 µV rms/Vdc为基准。这意味着:如果一个0 dB NI的电阻上有1 Vdc电压,则给定十倍频程时的过量噪声为1 µV rms。碳和厚膜电阻的NI最高,可能高达+10 dB左右,在信号路径的噪声敏感部分中最好避免使用。薄膜电阻一般要好得多,约为–20 dB;金属箔和绕线电阻可以低于–40 dB。
给定足够长的采集时间,均值法可将噪声降至无限小
一般认为均值法可将噪声降低均值数的平方根倍。这在一定条件下是成立的,即NSD必须保持平坦。然而,在1/f范围内和其他几种情况下,这种关系不成立。考虑在一个以恒定频率fs采样的系统中使用均值法,对n个样本求均值并进行1/n抽取,返回m个抽取样本。取n个平均值会将抽取后的有效采样速率变为fs/n,系统看到的有效最大频率降低n倍,白噪声降低√n倍。然而,获得m个样本的时间也会延长n倍,因此系统可以看到的最低频率也会降低n倍(记住,没有0 Hz这种事)。取的均值数越多,频段上的这些最大和最小频率就越往下移。一旦最大和最小频率均在1/f范围内,总噪声便仅取决于这些频率之比,再提高均值数对降低噪声没有进一步的好处。同样的道理也适用于多斜率等积分ADC的长积分时间。除了数学上的限制以外,还存在其他实际限制。例如,若量化噪声是主要噪声源,使得直流输入电压下的ADC输出为一个无闪烁的恒定码,则任何数量的均值都会返回同一个码 。

 举报
举报


 举报
举报

 举报
举报

 举报
举报

