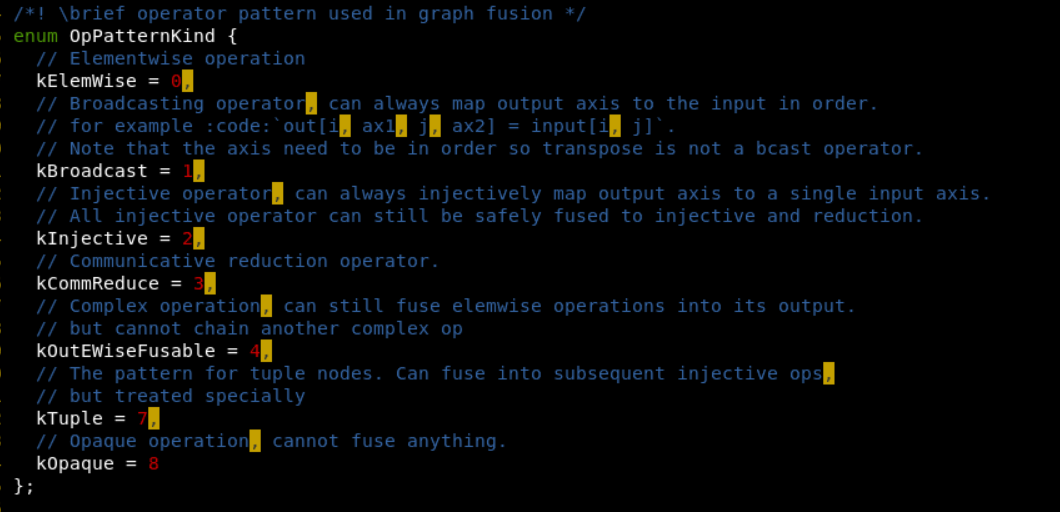
TVM中将计算算符分成四种:
1 injective。一一映射函数,比如加法,点乘等。
2 reduction。输入到输出具有降维性质的,比如sum。
3 complex-out。这是计算比较复杂的,比如卷积运算等。
4 opaque。无法被融合的算符,比如sort。
根据以上对算符的不同类型,TVM提供了三种融合规则:
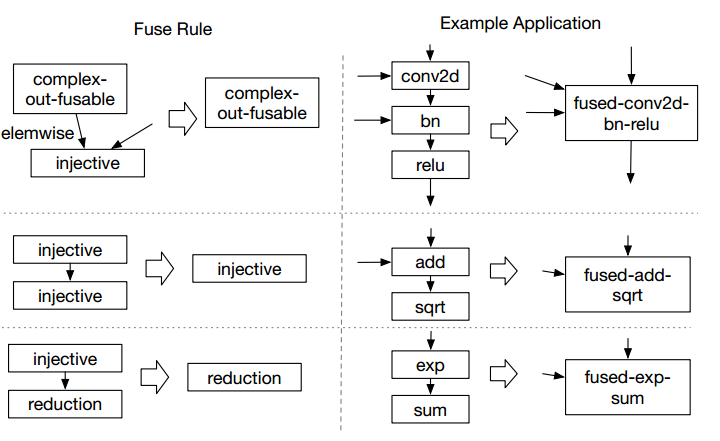
从一定角度看,这种融合实际上是数据计算pipeline化,即两次计算中间数据不再经历store-load的过程,而是直接给到下一个计算单元完成计算。
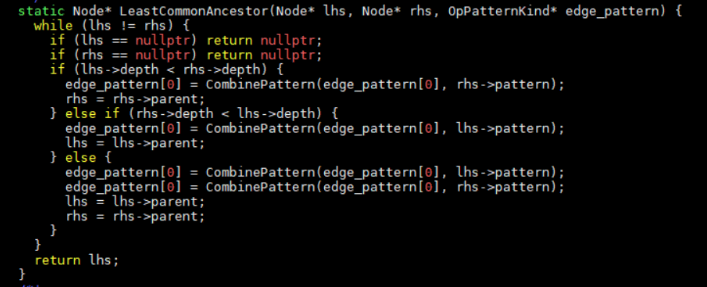
在走入fuse ops代码之前,还需要了解一些算法基础知识。算符融合中应用了支配树算法。在一个有向无环图中,对于一个节点n来说,从初始节点s出发到达n的所有路径都经历一个节点m,那么m就是n的支配点。而距离n最近的支配点被称作立即支配点。以r为树根,将所有立即支配点按照支配关系连接起来就形成了支配树。立即后支配点是从一个点n出发所有到终止节点的路径中通过的最近节点,形成的支配树是后支配树。
在DAG中,对于一个点,所有能到达它的点在支配树中的LCA,就是它支配树中的父亲。为什么算符融合要建立在后支配树的基础上呢?我猜测可能是因为对于两个可融合算符在DAG中位置分为两种,一种是父子关系,那么可以直接执行算符融合算法;另外一种是它们之间是后支配关系。对于具有后支配关系的两个节点(n-》m),就要判断未来路径上的节点是否都能够和点m发生融合,如果可以,那么n也可以和m发生融合。比如下图:
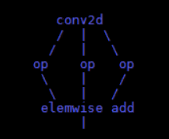
Conv2d要和elemwise add融合,必须判断它的三个op是否能和elemwise add融合。
TVM中融合流程分为三步:
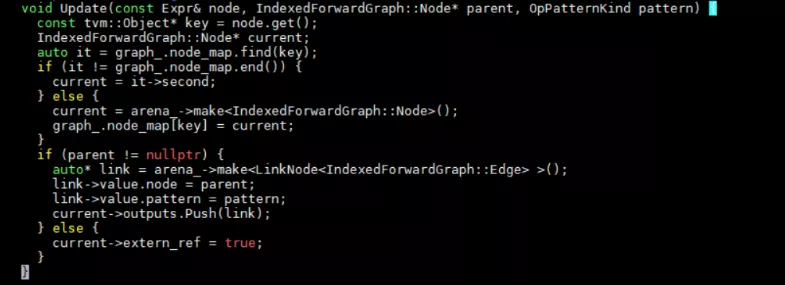
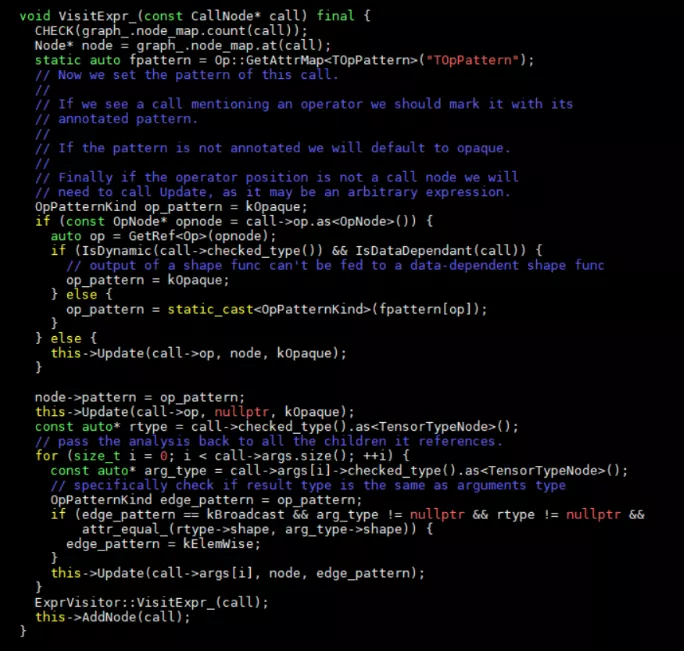
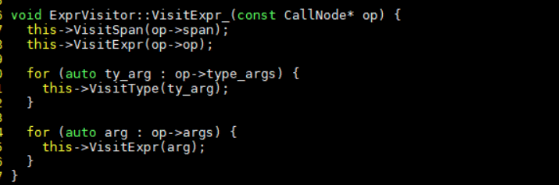
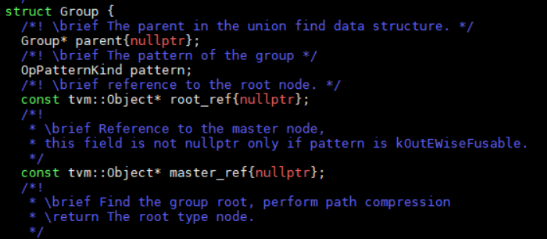
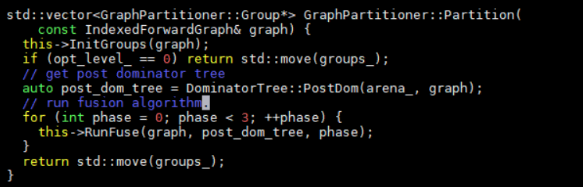
1 遍历relay树,建立DAG用于后支配树分析;
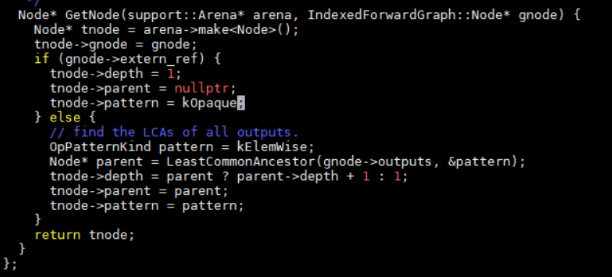
2 建立后支配树;
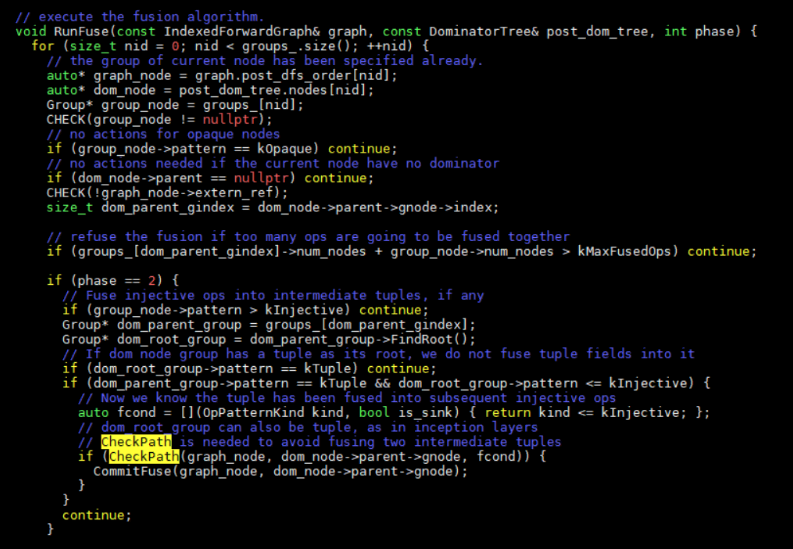
3 应用算符融合算法。
TVM中将计算算符分成四种:
1 injective。一一映射函数,比如加法,点乘等。
2 reduction。输入到输出具有降维性质的,比如sum。
3 complex-out。这是计算比较复杂的,比如卷积运算等。
4 opaque。无法被融合的算符,比如sort。
根据以上对算符的不同类型,TVM提供了三种融合规则:

从一定角度看,这种融合实际上是数据计算pipeline化,即两次计算中间数据不再经历store-load的过程,而是直接给到下一个计算单元完成计算。
在走入fuse ops代码之前,还需要了解一些算法基础知识。算符融合中应用了支配树算法。在一个有向无环图中,对于一个节点n来说,从初始节点s出发到达n的所有路径都经历一个节点m,那么m就是n的支配点。而距离n最近的支配点被称作立即支配点。以r为树根,将所有立即支配点按照支配关系连接起来就形成了支配树。立即后支配点是从一个点n出发所有到终止节点的路径中通过的最近节点,形成的支配树是后支配树。
在DAG中,对于一个点,所有能到达它的点在支配树中的LCA,就是它支配树中的父亲。为什么算符融合要建立在后支配树的基础上呢?我猜测可能是因为对于两个可融合算符在DAG中位置分为两种,一种是父子关系,那么可以直接执行算符融合算法;另外一种是它们之间是后支配关系。对于具有后支配关系的两个节点(n-》m),就要判断未来路径上的节点是否都能够和点m发生融合,如果可以,那么n也可以和m发生融合。比如下图:

Conv2d要和elemwise add融合,必须判断它的三个op是否能和elemwise add融合。
TVM中融合流程分为三步:
1 遍历relay树,建立DAG用于后支配树分析;
2 建立后支配树;
3 应用算符融合算法。

 举报
举报




 举报
举报

 举报
举报

 举报
举报

 举报
举报

