电磁力波的时间频率
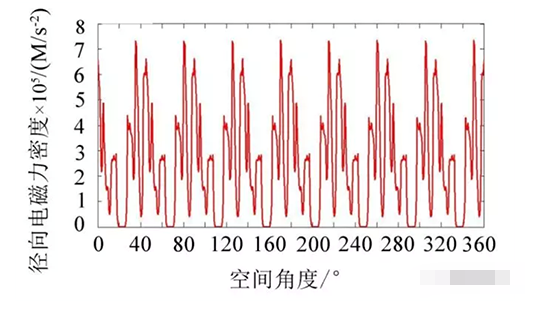
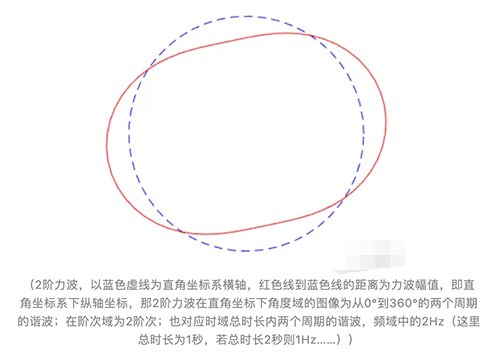
我们知道,电磁力波不仅仅是空间的函数,更是时间的函数,沿电机机械角度方向气隙各点的电磁力大小在随时间不停的变化,那么问题来了,我们一方面说电磁力波沿着空间分布有一定的形状,还给它取了个好听的名字叫“力型”,一方面又说沿电机圆周方向各点的电磁力大小随时间一直在变化,这个变化会打破他们的“队形”序列嘛?当然不会,当各点的电磁力幅值大小按照一定的相位和频率脉振时,宏观上来看,电磁力波的形状是不会改变的,但是它会旋转起来,这正是电磁力波随时间变化的体现。正是这些各个点的电磁力都按照同一频率和初始相位关系在不停的脉振变化,让电磁力形状得以保持,不停地匀速旋转,以电机二阶径向力波为例,来看看图6:

图6 二阶力波的变化过程
看了这个动图,相信大家对电磁力在时间和空间上的特性有了非常直观的了解,你会发现电磁力波的时间频率和所谓“力型”的转速之间是存在特定关系的,事实上它们和电机转速之间都存在着特定的关系,这都来源于电机电流随时间的变化,也正是它们之间这些特定的关系(电磁力波频率与电机转速的特定关系),让我们可以在测试瀑布图上能够以阶次特征捕捉到这些电磁力波。
电磁力波的时间频率
我们知道,电磁力波不仅仅是空间的函数,更是时间的函数,沿电机机械角度方向气隙各点的电磁力大小在随时间不停的变化,那么问题来了,我们一方面说电磁力波沿着空间分布有一定的形状,还给它取了个好听的名字叫“力型”,一方面又说沿电机圆周方向各点的电磁力大小随时间一直在变化,这个变化会打破他们的“队形”序列嘛?当然不会,当各点的电磁力幅值大小按照一定的相位和频率脉振时,宏观上来看,电磁力波的形状是不会改变的,但是它会旋转起来,这正是电磁力波随时间变化的体现。正是这些各个点的电磁力都按照同一频率和初始相位关系在不停的脉振变化,让电磁力形状得以保持,不停地匀速旋转,以电机二阶径向力波为例,来看看图6:

图6 二阶力波的变化过程
看了这个动图,相信大家对电磁力在时间和空间上的特性有了非常直观的了解,你会发现电磁力波的时间频率和所谓“力型”的转速之间是存在特定关系的,事实上它们和电机转速之间都存在着特定的关系,这都来源于电机电流随时间的变化,也正是它们之间这些特定的关系(电磁力波频率与电机转速的特定关系),让我们可以在测试瀑布图上能够以阶次特征捕捉到这些电磁力波。

 举报
举报



 举报
举报





 举报
举报


 举报
举报

