麦克斯韦方程组
麦克斯韦方程组是英国物理学家詹姆斯·麦克斯韦,在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程,它有两种表达形式。
1.积分形式

H表示磁场强度矢量;
E表示媒质中感应出的电场强度;
B为磁感应强度;D为电位移矢量;
J—电流密度矢量;dl—曲线C上的长度元矢量;
dS为以曲线C为周界的面积元矢量;dt为时间元;
ρ表示体积V内的电荷密度。
方程1的物理含义:沿曲线C的传导电流和位移电流之和是以曲线C为周界的磁场强度为H的磁场的源;
方程2的物理含义:磁感应强度为场B的磁场在沿曲线C的回路中产生的感应电动势为以曲线C为周界的磁通量的变化率;
方程3表示磁场是无源场,穿过任意闭合曲面的磁感应强度的通量为零,暗示了磁单极子不存在;
方程4表示电荷守恒定律,即通过任意闭合曲面的电位移通量等于该闭合面所包围的自由电荷的代数和。
2.微分形式
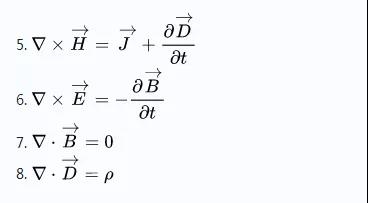
3.辅助方程

ε — 介电常数; μ — 为磁导率;
σ — 媒质的电导率。
麦克斯韦方程组
麦克斯韦方程组是英国物理学家詹姆斯·麦克斯韦,在19世纪建立的一组描述电场、磁场与电荷密度、电流密度之间关系的偏微分方程,它有两种表达形式。
1.积分形式

H表示磁场强度矢量;
E表示媒质中感应出的电场强度;
B为磁感应强度;D为电位移矢量;
J—电流密度矢量;dl—曲线C上的长度元矢量;
dS为以曲线C为周界的面积元矢量;dt为时间元;
ρ表示体积V内的电荷密度。
方程1的物理含义:沿曲线C的传导电流和位移电流之和是以曲线C为周界的磁场强度为H的磁场的源;
方程2的物理含义:磁感应强度为场B的磁场在沿曲线C的回路中产生的感应电动势为以曲线C为周界的磁通量的变化率;
方程3表示磁场是无源场,穿过任意闭合曲面的磁感应强度的通量为零,暗示了磁单极子不存在;
方程4表示电荷守恒定律,即通过任意闭合曲面的电位移通量等于该闭合面所包围的自由电荷的代数和。
2.微分形式
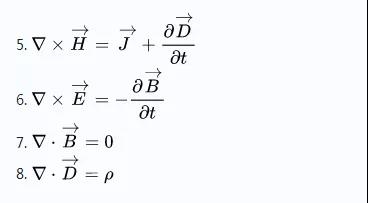
3.辅助方程

ε — 介电常数; μ — 为磁导率;
σ — 媒质的电导率。

 举报
举报




 举报
举报

 举报
举报

 举报
举报

 举报
举报

