通用量子计算机
从算法的角度来说,量子计算机具有比经典计算机更强大的计算能力。这个想法最初是由费曼(R。 Feynman)和马宁(Y。 Manin)在20世纪80年代初提出[1, 2]。自20世纪40年代美国核武器研究起,数值计算被广泛应用于物理学以及其他学科的研究中。
其中重要的一项应用是对物理系统的数值模拟。自然界的物理系统均为量子系统。然而,由于记录和处理量子态需要很大的信息存储空间,利用经典计算机对量子多体系统进行模拟是非常困难的。但是,量子计算机没有这个问题。如果经典计算机无法精确模拟量子多体系统而量子计算机可以,那么不言而喻,量子计算机优于经典计算机。
1985年,多伊奇(D。 Deutsch)提出了量子计算机的模型——通用量子计算机(或量子图灵机)[4]。任意一种量子算法均可以利用通用量子计算机实现。量子计算机是由许多量子比特(二态量子系统)组成的物理系统。
对每个量子比特, |0》 和|1》是两个完全可区分的量子态,它们分别对应二进制数中的0 和1。量子比特和经典比特的差别在于,量子比特可以处于0 和1 的量子叠加态,用a|0》 +b |1》 表示,这里系数a 和b 刻画了量子比特的具体状态。量子计算有很多方式,其中广泛使用的模型是量子线路,也就是通过在量子比特上执行一系列的逻辑操作来实现量子计算,如图1所示。这些逻辑操作包括:量子比特的初始化、量子态的幺正变换以及对量子比特信息的读取。
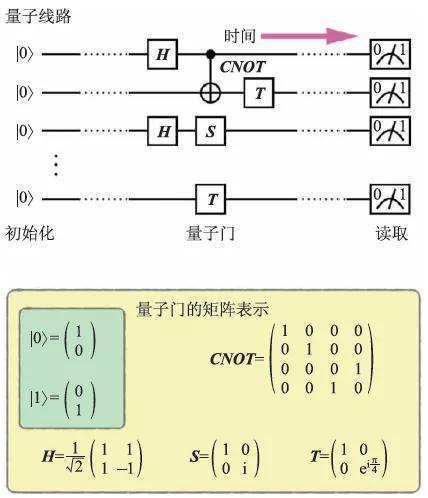
图1 量子线路和量子门。量子线路由量子比特的初始化、一组量子门以及最终的信息读取组成。其中的量子门可以由矩阵表示
与经典计算机中的通用逻辑门类似,在量子计算机中任意的幺正变换均可以通过一组有限的幺正变换(量子门)的组合以任意的精确度近似。这样一组量子门被称为通用量子门。
例如,Hadamard门(H)、π/4 相位门(S)、π/8 相位门(T)以及受控非门(CNOT)构成一组通用量子门[5]。这里面H、S 和T为单量子比特门,CNOT为两量子比特门(图1)。利用这些量子门,不仅可以实现任意的量子算法,还可以实现任意的经典算法。从这个意义上说,显然量子计算机的计算能力是大于等于经典计算机的。
1986年,多伊奇和乔沙(R。 Jozsa)提出了一个计算问题来表明量子计算机的确在解决某些问题上具有优势[6]。他们提出的问题是判断一个函数f :{x}→{0,1}对于不同的输入x 是否给出相同的输出0 或1。函数f 需要满足一定的条件,这里不再赘述。
对于输入为一个比特的情况,也就是x有两个取值0 和1,用经典计算机解决这个问题需要计算f 至少两次。而用量子计算机只需要计算f一次, 这个量子算法被称为多伊奇— 乔沙(Deutsch—Jozsa)算法。当输入比特增多的时候,确定性经典算法需要计算f 的次数随着比特数量指数增长,而量子算法仍然只需要计算f 一次。
通用量子计算机
从算法的角度来说,量子计算机具有比经典计算机更强大的计算能力。这个想法最初是由费曼(R。 Feynman)和马宁(Y。 Manin)在20世纪80年代初提出[1, 2]。自20世纪40年代美国核武器研究起,数值计算被广泛应用于物理学以及其他学科的研究中。
其中重要的一项应用是对物理系统的数值模拟。自然界的物理系统均为量子系统。然而,由于记录和处理量子态需要很大的信息存储空间,利用经典计算机对量子多体系统进行模拟是非常困难的。但是,量子计算机没有这个问题。如果经典计算机无法精确模拟量子多体系统而量子计算机可以,那么不言而喻,量子计算机优于经典计算机。
1985年,多伊奇(D。 Deutsch)提出了量子计算机的模型——通用量子计算机(或量子图灵机)[4]。任意一种量子算法均可以利用通用量子计算机实现。量子计算机是由许多量子比特(二态量子系统)组成的物理系统。
对每个量子比特, |0》 和|1》是两个完全可区分的量子态,它们分别对应二进制数中的0 和1。量子比特和经典比特的差别在于,量子比特可以处于0 和1 的量子叠加态,用a|0》 +b |1》 表示,这里系数a 和b 刻画了量子比特的具体状态。量子计算有很多方式,其中广泛使用的模型是量子线路,也就是通过在量子比特上执行一系列的逻辑操作来实现量子计算,如图1所示。这些逻辑操作包括:量子比特的初始化、量子态的幺正变换以及对量子比特信息的读取。

图1 量子线路和量子门。量子线路由量子比特的初始化、一组量子门以及最终的信息读取组成。其中的量子门可以由矩阵表示
与经典计算机中的通用逻辑门类似,在量子计算机中任意的幺正变换均可以通过一组有限的幺正变换(量子门)的组合以任意的精确度近似。这样一组量子门被称为通用量子门。
例如,Hadamard门(H)、π/4 相位门(S)、π/8 相位门(T)以及受控非门(CNOT)构成一组通用量子门[5]。这里面H、S 和T为单量子比特门,CNOT为两量子比特门(图1)。利用这些量子门,不仅可以实现任意的量子算法,还可以实现任意的经典算法。从这个意义上说,显然量子计算机的计算能力是大于等于经典计算机的。
1986年,多伊奇和乔沙(R。 Jozsa)提出了一个计算问题来表明量子计算机的确在解决某些问题上具有优势[6]。他们提出的问题是判断一个函数f :{x}→{0,1}对于不同的输入x 是否给出相同的输出0 或1。函数f 需要满足一定的条件,这里不再赘述。
对于输入为一个比特的情况,也就是x有两个取值0 和1,用经典计算机解决这个问题需要计算f 至少两次。而用量子计算机只需要计算f一次, 这个量子算法被称为多伊奇— 乔沙(Deutsch—Jozsa)算法。当输入比特增多的时候,确定性经典算法需要计算f 的次数随着比特数量指数增长,而量子算法仍然只需要计算f 一次。

 举报
举报


 举报
举报

 举报
举报


 举报
举报

 举报
举报

