1. 最大权闭合子图
目标:
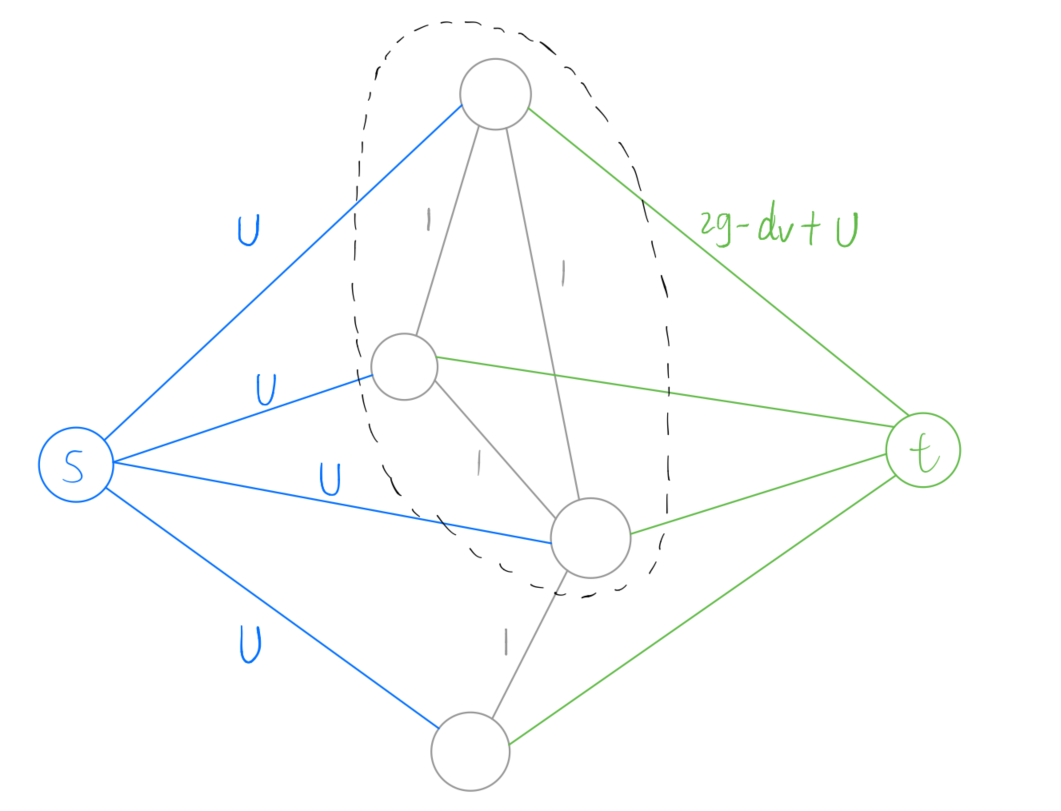
最大化 /(f = |E| - g|V|/)
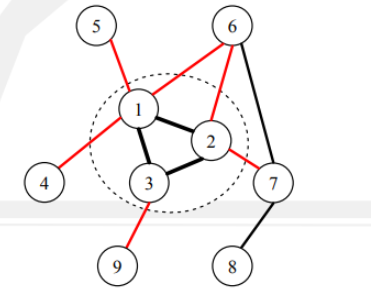
把无向边 /((u,v)/) 看做一个点连接两条有向边指向 /(u/) 和 /(v/) 原图的点权值设为 /(-g/) ,
边的点为 /(1/) ,这样就转成了最大权闭合子图的问题
1. 最大权闭合子图
目标:
最大化 /(f = |E| - g|V|/)
把无向边 /((u,v)/) 看做一个点连接两条有向边指向 /(u/) 和 /(v/) 原图的点权值设为 /(-g/) ,
边的点为 /(1/) ,这样就转成了最大权闭合子图的问题

 举报
举报


 举报
举报

 举报
举报

 举报
举报

