参考文献:
1. Standard IPC-2141A, "Controlled Impedance Circuit Boards and High Speed Logic Design," 2004, Institute for Interconnection and Packaging Electronic Circuits, 3000 Lakeside Drive, 309 S, Bannockburn, IL 60015, 847-615-7100.
2. Eric Bogatin, BTS015, PCB Impedance Design: Beyond the IPC Recommendations, BeTheSignal.com.
3. Eric Bogatin, Signal Integrity – Simplified, Prentice Hall PTR, 2003, ISBN-10: 0130669466, ISBN-13: 978-0130669469.
4. Andrew Burkhardt, Christopher Gregg, Alan Staniforth, "Calculation of PCB Track Impedance," Technical Paper S-19-5, presented at the IPC Printed Circuits Expo '99 Conference, March 14–18, 1999.
5. Brian C. Wadell, Transmission Line Design Handbook, Artech House, Norwood, MA, 1991, ISBN: 0- 89006-436-9.
6. William R. Blood, Jr., MECL System Design Handbook (HB205/D, Rev. 1A May 1988), ON Semiconductor, August, 2000.
7. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 12
8. Walt Kester, Analog-Digital Conversion, Analog Devices, 2004, ISBN 0-916550-27-3, Chapter 9. Also available as The Data Conversion Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7841-0, Chapter 9.
9. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Chapter 7. Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 7.来源:Analog Devices, Inc.
参考文献:
1. Standard IPC-2141A, "Controlled Impedance Circuit Boards and High Speed Logic Design," 2004, Institute for Interconnection and Packaging Electronic Circuits, 3000 Lakeside Drive, 309 S, Bannockburn, IL 60015, 847-615-7100.
2. Eric Bogatin, BTS015, PCB Impedance Design: Beyond the IPC Recommendations, BeTheSignal.com.
3. Eric Bogatin, Signal Integrity – Simplified, Prentice Hall PTR, 2003, ISBN-10: 0130669466, ISBN-13: 978-0130669469.
4. Andrew Burkhardt, Christopher Gregg, Alan Staniforth, "Calculation of PCB Track Impedance," Technical Paper S-19-5, presented at the IPC Printed Circuits Expo '99 Conference, March 14–18, 1999.
5. Brian C. Wadell, Transmission Line Design Handbook, Artech House, Norwood, MA, 1991, ISBN: 0- 89006-436-9.
6. William R. Blood, Jr., MECL System Design Handbook (HB205/D, Rev. 1A May 1988), ON Semiconductor, August, 2000.
7. Hank Zumbahlen, Basic Linear Design, Analog Devices, 2006, ISBN: 0-915550-28-1. Also available as Linear Circuit Design Handbook, Elsevier-Newnes, 2008, ISBN-10: 0750687037, ISBN-13: 978-0750687034. Chapter 12
8. Walt Kester, Analog-Digital Conversion, Analog Devices, 2004, ISBN 0-916550-27-3, Chapter 9. Also available as The Data Conversion Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7841-0, Chapter 9.
9. Walter G. Jung, Op Amp Applications, Analog Devices, 2002, ISBN 0-916550-26-5, Chapter 7. Also available as Op Amp Applications Handbook, Elsevier/Newnes, 2005, ISBN 0-7506-7844-5. Chapter 7.来源:Analog Devices, Inc.

 举报
举报

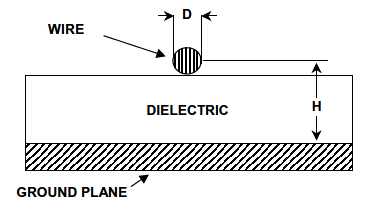
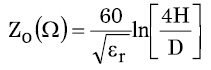 等式2
等式2
 举报
举报
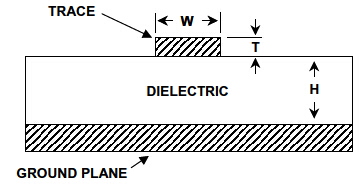
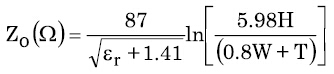 等式3
等式3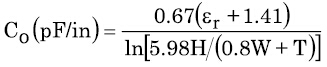 等式4
等式4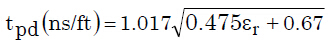 等式5
等式5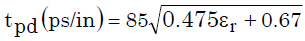 等式6
等式6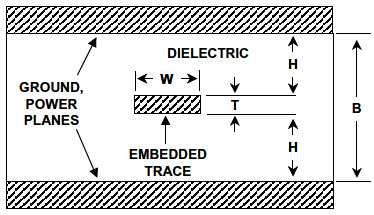
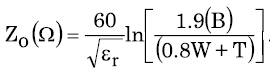 等式7
等式7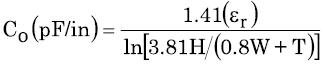 等式8
等式8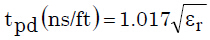 等式9
等式9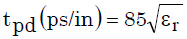 等式10
等式10

 举报
举报

 举报
举报

