卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
斯坦利·施密特(Stanley Schmidt)首次实现了卡尔曼滤波器。卡尔曼在NASA埃姆斯研究中心访问时,发现他的方法对于解决阿波罗计划的轨道预测很有用,后来阿波罗飞船的导航电脑使用了这种滤波器。 关于这种滤波器的论文由Swerling (1958), Kalman (1960)与 Kalman and Bucy (1961)发表。
数据滤波是去除噪声还原真实数据的一种数据处理技术, Kalman滤波在测量方差已知的情况下能够从一系列存在测量噪声的数据中,估计动态系统的状态。 由于, 它便于计算机编程实现, 并能够对现场采集的数据进行实时的更新和处理, Kalman滤波是目前应用最为广泛的滤波方法, 在
通信, 导航, 制导与控制等多领域得到了较好的应用。
性质
①卡尔曼滤波是一个算法,它适用于线性、离散和有限维系统。每一个有外部变量的自回归移动平均系统(ARMAX)或可用有理传递函数表示的系统都可以转换成用状态空间表示的系统,从而能用卡尔曼滤波进行计算。
②任何一组观测数据都无助于消除x(t)的确定性。增益K(t)也同样地与观测数据无关。
③当观测数据和状态联合服从高斯分布时用卡尔曼递归公式计算得到的是高斯随机变量的条件均值和条件方差,从而卡尔曼滤波公式给出了计算状态的条件概率密度的更新过程线性最小方差估计,也就是最小方差估计。
卡尔曼滤波理解及代码分析
鉴于网上的代码以及分析的各种错误,所以写一个正确的详细的分析。
过程方程以及量测方程
X(K)=AX(K-1)+BU(K-1)+W(K-1)
Z(K)=HX(K)+V(K)
说明,下面带T的表示转置。
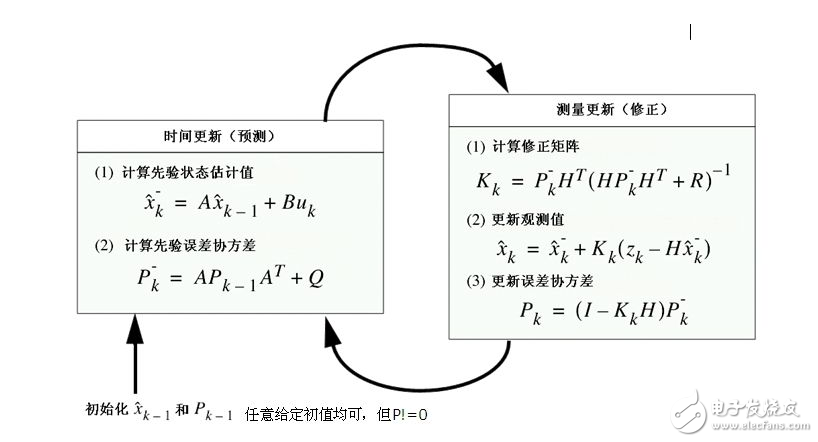
卡尔曼滤波的黄金五条公式
X(k|k-1)=AX(k-1|k-1)+BU(k)………。先验估计
P(k|k-1)=A P(k-1| k-1) AT+Q………。误差协方差
Kg(k)= P(k|k-1) HT / (H P(k|k-1) HT + R)………。计算卡尔曼增益
X(k|k)= X(k|k-1) + Kg(k)(Z(k) - H X(k|k-1))………。修正估计
P(k|k)=( I-Kg(k) H) P(k|k-1)………。更新误差协方差
下面的程序主要针对MPU6050的姿态角的滤波。
float Q_angle=0.001; //陀螺仪噪声的协方差
float Q_gyro=0.003; //陀螺仪漂移噪声的协方差
float R_angle=0.5; // 加速度计的协方差
float dt=0.005;
char C_0 = 1;
float Q_bias=0, Angle_err=0; //Q_bias为陀螺仪漂移
float PCt_0=0, PCt_1=0, E=0;
float K_0=0, K_1=0, t_0=0, t_1=0;
float Pdot[4] ={0,0,0,0};
float PP[2][2] = { { 1, 0 },{ 0, 1 } };12345678910
首先建立的是过程方程,这里的状态变量是angle以及Q_bias,角度以及陀螺仪的漂移。

那么已经建立了这里的预测方程,没有加上噪声。
void Kalman_Filter(float Gyro,float Accel)
{ //Gyro陀螺仪的测量值,Accel加速度计的角度计算值
Angle+=(Gyro - Q_bias) * dt;
//角度测量模型方程
//就漂移来说认为每次都是相同的Q_bias=Q_bias;
//由此得到矩阵1234567
上面的代码就对应着预测方程。对应着卡尔曼滤波的五个公式的第一条:X(k|k-1)=AX(k-1|k-1)+BU(k)
这里再分析第二条公式,P(k|k-1)=A P(k-1| k-1) AT+Q。可以在之前看出,A=[1,-dt;0,1]。而Q的定义如下:

因为角度噪声和陀螺仪的角速度的漂移噪声相互独立,所以为一个对角矩阵。然后,Q_angle,Q_gyro再程序开头已经给出。所以设P=[a,b;c,d]
的出一个更新的式子,
[acbd]=[10−dt1][acbd][1−dt01]+[Qangle00Qgyro]
最后的到的更新的方法
[acbd]=[a−c∗dt−b∗dt+d∗dt∗dtc−d∗dtb−d∗dtd]+[Qangle00Qgyro]
所以看代码,可以看出写的极为的不合理,但是都是这样写的,先看一看。
Pdot[0]=Q_angle - PP[0][1] - PP[1][0];
Pdot[1] = -PP[1][1];
Pdot[2] = -PP[1][1];
Pdot[3] = Q_gyro;
PP[0][0] += Pdot[0] * dt;
PP[0][1] += Pdot[1] * dt;
PP[1][0] += Pdot[2] * dt;
PP[1][1] += Pdot[3] * dt;123456789
对照上面的公式,还是可以看出来,PP就是[a,b;c,d]的,但是注意,Pdot只是矩阵运算的中间值,但是不知为什么要叫成Pdot,误人子弟。而且最大的错误在于这样写,Q乘以了一个dt,但是最后并不会怎么影响,因为Q也是初始给的一个值而已,但是这样写还是有问题的,还是按照推导来写比较好。
再是第三个公式来计算卡尔曼增益,Kg(k)= P(k|k-1) HT / (H P(k|k-1) HT + R),所以这里要做的就是再建立一个量测方程,这里测量的值是加速度计算出来的角度值,所以
Accelangle=[10][angleQbias]+R
所以H=[1 0],卡尔曼增益就是一个二维向量[k0,k1]T。
直接带入计算第三个公式。
PCt_0 = C_0 * PP[0][0];//矩阵乘法的中间变量
PCt_1 = C_0 * PP[1][0];//C_0=1
//分母
E = R_angle + C_0 * PCt_0;
//增益值
K_0 = PCt_0 / E;
K_1 = PCt_1 / E; 1234567
基本还算比较清楚,但是命名的话真的不忍心吐槽。
再看第四个公式,X(k|k)= X(k|k-1) + Kg(k)(Z(k) - H X(k|k-1))。
Angle_err = Accel - Angle; //Accel是加速度计的值,算出来的角度的测量值。
Angle += K_0 * Angle_err; //对状态的卡尔曼估计。
Q_bias += K_1 * Angle_err;
Gyro_x = Gyro - Q_bias; //计算得角速度值,这里由于每次对Q_bias更新,就更准确,比初始矫正后不管肯定要好很多。123456
第五个公式对PP进行更新,P(k|k)=( I-Kg(k) H) P(k|k-1);
t_0 = PCt_0; //矩阵计算中间变量
t_1 = C_0 * PP[0][1];
PP[0][0] -= K_0 * t_0;
PP[0][1] -= K_0 * t_1;
PP[1][0] -= K_1 * t_0;
PP[1][1] -= K_1 * t_1;
}12345678
已经不忍心吐槽他的命名了。到这里基本分析完毕,至于卡尔曼滤波的证明推导,可以参考其他,这里只是分析代码,但是网上基本都是这样写的,有分析的,但是要么就是直接甩代码,要么就是分析的很多错误,太乱,决定写一个完整的正确的分析mpu6050卡尔曼滤波的程序。





